Numero complesso coniugato
Quando due numeri complessi hanno lo stesso valore nella parte reale (a) e il coefficiente immaginario (b) di pari valore ma segno opposto sono detti numeri complessi coniugati. $$ z=a+bi $$ $$ z'=a-bi $$
Tutti i numeri complessi sono associati a un numero complesso coniugato, ad eccezione del numero complesso z =(0,0).
Se a=0 e b=0 non è possibile calcolare il coniugato.
La differenza tra numeri complessi coniugati e opposti. I numeri z=2+3i e z'=2-3i sono coniugati tra loro. $$ z=2+3i \\ z'=2-3i $$ I numeri z=2+3i e z'=-2-3i non sono coniugati tra loro perché anche la parte reale ha segno opposto. In quest'ultimo caso i due numeri cono detti numeri complessi opposti. $$ z=2+3i \\ z'=-2-3i $$ Infine, i numeri z=2+3i e z'=-2+3i non sono né coniugati, né opposti perché solo la parte reale ha cambiato segno. $$ z=2+3i \\ z'=-2+3i $$
Un esempio pratico
Ho il numero complesso
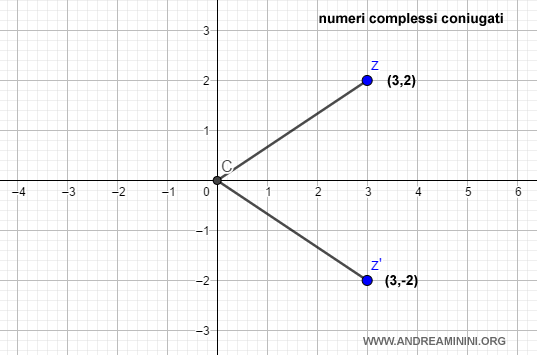
$$ z=3+2i $$
Il numero complesso coniugato è
$$ z'=3-2i $$
Dal punto di vista grafico il numero complesso coniugato si presenta riflesso sull'asse delle ascisse.
Le proprietà dei numeri complessi coniugati
Alcune proprietà dei numeri complessi coniugati
- La somma di due numeri coniugati z=a+bi e z'=a-bi è un numero reale 2a $$ z+z' = 2a $$
Dimostrazione. Considero un numero complesso z=a+bi con parte reale e immaginaria non nulle. Il numero complesso coniugato è z' = a-bi $$ z=a+bi \\ z'=a-bi $$ La somma dei numeri complessi coniugati è $$ z+z' = (a+bi)+(a-bi) = a+bi+a-bi = 2a $$
- La differenza tra due numeri complessi coniugati z=a+bi e z'=a-bi è un numero immaginario 2bi $$ z-z' = 2bi $$
Dimostrazione. Considero due numeri complessi coniugati z=a+bi e z'=a-bi. $$ z=a+bi \\ z'=a-bi $$ La differenza dei numeri complessi è un numero immaginario pari al doppio del coefficiente della parte immaginaria del minuendo. $$ z-z' = (a+bi)-(a-bi) $$ $$ z-z' = a+bi-a+bi $$ $$ z-z' = 2bi $$
- Il prodotto tra due numeri complessi coniugati z=a+bi e z'=a-bi è un numero reale a2+b2 $$ z \cdot z' = a^2 + b^2 $$
Dimostrazione. Considero il numero complesso z=a+bi e il suo coniugato z'=a-bi $$ z=a+bi \\ z'=a-bi $$ Moltiplico tra loro i due numeri coniugati $$ z \cdot z' = (a+bi)\cdot(a-bi) $$ $$ z \cdot z' = a^2-abi+abi-b^2i^2 $$ $$ z \cdot z' = a^2-b^2i^2 $$ Sapendo che il quadrato dell'unità immaginaria è i2=-1 $$ z \cdot z' = a^2-b^2(-1) $$ $$ z \cdot z' = a^2+b^2 $$ Quindi, il prodotto di due numeri complessi coniugati è la somma del quadrato della parte reale e del quadrato del coefficiente della parte immaginaria.
E così via.
