La forma algebrica dei numeri complessi

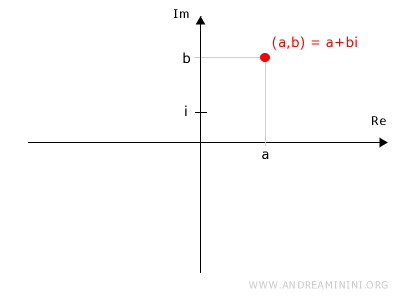
Un numero complesso (a,b) può essere scritto anche in forma algebrica come somma di un numero reale (a) e di un numero immaginario (bi) $$ (a,b) = a + b \cdot i $$

Dove $ i $ è l'unità immaginaria i=(0,1) mentre a,b sono due numeri reali.

Il termine $ a $ è detto parte reale mentre il termine $b \cdot i$ è detto parte immaginaria del numero complesso, dove $ b $ è il coefficiente della parte immaginaria.

La forma algebrica è anche detta forma compatta dei numeri complessi.

Nota. La forma algebrica è soltanto una delle rappresentazioni possibili di un numero complesso. Altre rappresentazioni sono la forma trigonometrica e la forma esponenziale.

Se la parte reale $ a $ è nulla, il numero compleso $ z=a+bi $ è detto numero immaginario.

Ad esempio, z=3i è un numero immaginario.

$$ z = 3i $$

Se, invece, ad essere nulla è il coefficiente della parte immaginaria $ b=0 $, allora il numero complesso  $ z=a+bi $ è detto numero reale.

Ad esempio, z=5 è un numero reale.

$$ z=5 $$

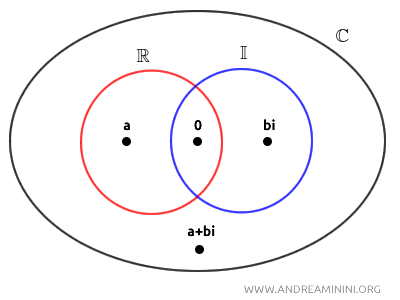
Quindi, l'insieme dei numeri complessi ( $ \mathbb{C} $ ) ha come sottoinsiemi sia i numeri reali ( $ \mathbb{R} $ ) che i numeri immaginari puri ( $ \mathbb{I} $ ).

Tuttavia, non è semplicemente l'unione di questi due sottoinsiemi. E' più grande.

Nota. L'insieme dei numeri complessi è più grande dell'unione dei numeri reali e immaginari puri perché contiene tutte le possibili combinazioni di parte reale e parte immaginaria, mentre l'unione dei numeri reali e immaginari puri contiene solo i numeri con \( a = 0 \) o \( b = 0 \).

Un esempio pratico

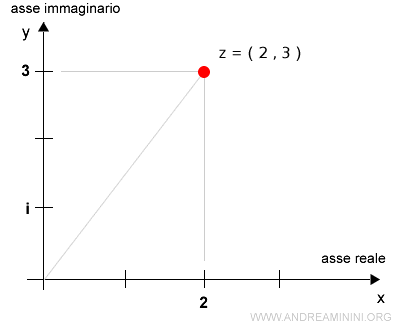
Prendo in considerazione il numero complesso (2,3)

$$ (a,b) = (2,3) $$

La parte reale del numero complesso è a=2 mentre la parte immaginaria è b=3.

La forma algebrica del numero complesso (2,3) è

$$ (2,3) = 2 + 3i $$

Sul piano di Gauss è lo stesso punto.

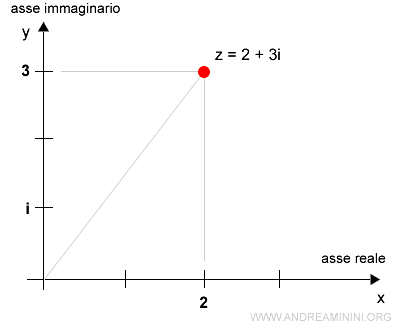
Quindi, se scrivo (2,3) o 2+3i indico lo stesso numero complesso.

Sono soltanto due modi diversi per rappresentare lo stesso numero.

Nota. Ogni punto (x,y) del piano di Gauss è un numero complesso e viceversa. Il numero complesso alle coordinate (2,3) posso scriverlo in forma algebrica 2+3i.

Le operazioni tra i numeri complessi in forma algebrica

I numeri complessi in forma algebrica \(a + bi\), con \(a\) e \(b\) numeri reali e \(i\) definito come l'unità immaginaria (\(i^2 = -1\)), hanno una struttura simile a quella di un binomio.

Questo significa che le operazioni algebriche eseguite sui numeri complessi, come addizione, sottrazione, moltiplicazione e divisione, seguono regole simili a quelle applicabili ai binomi nell'algebra tradizionale.

Operazioni di base con i numeri complessi

• Addizione e sottrazione
  Si sommano o sottraggono i termini reali e immaginari separatamente: $$ (a + bi) + (c + di) = (a + c) + (b + d)i $$ $$
  (a + bi) - (c + di) = (a - c) + (b - d)i $$

  Esempio: $$ (3 + 2i) + (1 - 4i) = (3 + 1) + (2 - 4)i = 4 - 2i $$

• Moltiplicazione
  La moltiplicazione tra due numeri complessi segue la regola distributiva, ricordando che \(i^2 = -1\): $$ (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i
  $$

  Esempio: $$ (2 + 3i)(1 + 4i) = 2 + 8i + 3i + 12i^2 = 2 + 11i - 12 = -10 + 11i $$

• Coniugato
  Il coniugato di un numero complesso si ottiene invertendo il segno della parte immaginaria: $$ \overline{a + bi} = a - bi $$

  Esempio: Per \(3 + 4i\), il coniugato è \(3 - 4i\).

• Divisione
  Per dividere due numeri complessi, si moltiplica numeratore e denominatore per il complesso coniugato del denominatore: $$ \frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} $$

  Esempio: $$ \frac{3 + 2i}{1 - i} = \frac{(3 + 2i)(1 + i)}{(1 - i)(1 + i)}  $$ $$ = \frac{3 + 3i + 2i + 2i^2}{1^2 - i^2} $$ $$ = \frac{3 + 5i - 2}{1 + 1} $$ $$ = \frac{1 + 5i}{2} $$ $$ = 0.5 + 2.5i $$

• Modulo
  Il modulo di un numero complesso \(a + bi\) è la sua distanza euclidea dal centro del piano di Gauss. Si calcola usando il teorema di Pitagora. $$ |a + bi| = \sqrt{a^2 + b^2} $$
  

  Esempio: Per \(3 + 4i\), il modulo è \(\sqrt{3^2 + 4^2} = 5\).

L'utilizzo di queste regole mi consente di trattare i numeri complessi come estensioni naturali dei numeri reali.

La dimostrazione

Qualsiasi numero complesso (a,b) posso vederlo come somma di un numero complesso reale (a,0) e di un numero immaginario (0,b)

$$ (a,b) = (a,0) + (0,b) $$

A sua volta il numero immaginario posso scriverlo come il prodotto del numero reale (b,0) per l'unità immaginaria (0,1) ossia (0,b)=(b,0)·(0,1)

$$ (a,b) = (a,0) + [ (b,0) \cdot (0,1) ] $$

Il simbolo dell'unità immaginaria è i=(0,1)

$$ (a,b) = (a,0) + [ (b,0) \cdot i ] $$

Il numero (b,0) è un numero reale b=(b,0) perché la parte immaginaria è nulla.

$$ (a,b) = (a,0) + [ b \cdot i ] $$

Anche il numero (a,0) è un numero reale a=(a,0)

$$ (a,b) = a + [ b \cdot i ] $$

Il risultato finale è la forma algebrica a+b·i del numero complesso (a,b)

$$ (a,b) = a + b \cdot i $$

Il termine a è la parte reale del numero complesso (a,b) mentre il termine b·i è la parte immaginaria.

Il termine b è un numero reale detto coefficiente della parte immaginaria.

Nota. Qualsiasi numero reale può essere scritto in forma algebrica ponendo b=0. $$ a + 0 \cdot i $$ Allo stesso modo, ogni numero immaginario può essere scritto in forma algebrica ponendo a=0. $$ 0 + b \cdot i $$ Da questo deduco che i numeri reali e i numeri immaginari sono sottoinsiemi propri dei numeri complessi.

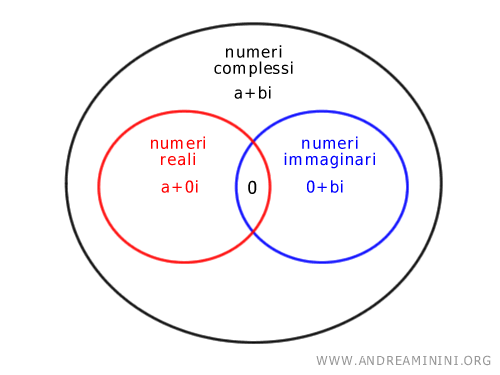
L'insieme dei numeri reali e l'insieme dei numeri immaginari hanno in comune soltanto il numero complesso (0,0) ossia l'origine del piano di Gauss che può essere considerato sia un numero reale che un numero immaginario.

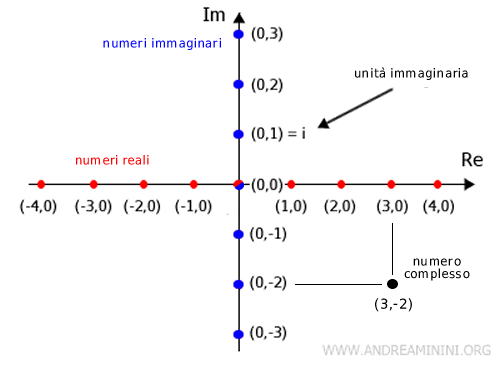
I numeri reali corrispondono ai punti dell'asse dell'ascissa mentre i numeri immaginari ai punti dell'asse delle ordinate. In generale, ogni punto del piano (x,y) è un numero complesso. Quindi, l'insieme dei numeri complessi è molto più grande dell'unione dei numeri reali e dei numeri immaginari.

E così via.