La divisione di due numeri complessi in forma esponenziale
Dati due numeri complessi in forma esponeziale z1=r1eiα e z2=r2eiβ , il quoziente z1/z2 è un numero complesso che per modulo il quoziente dei moduli r1/r2 e per argomento la differenza degli argomenti α-β. $$ \frac{z_1}{z_2} = \frac{r_1 \cdot e^{i \alpha }}{r_2 \cdot e^{i \beta}} = ( \frac{r_1}{r_2} ) \cdot e^{i(\alpha-\beta)} $$
Un esempio pratico
Considero due numeri complessi
$$ z_1=1+3i $$
$$ z_2=4+2i $$
Sul piano di Gauss i due numeri sono i punti (1,3) e (4,2)
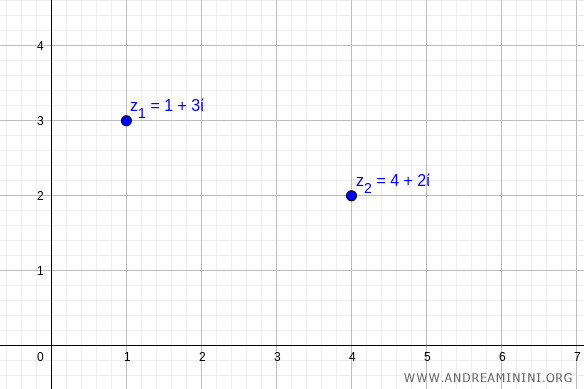
Trasformo ii due numeri complessi nella forma trigonometrica
Calcolo il modulo dei due numeri complessi
$$ r_1 = \sqrt{1^2+3^2} = \sqrt{10} = 3.16 $$
$$ r_2 = \sqrt{4^2+2^2} = \sqrt{20} = 4.47 $$
Poi calcolo l'argomento dei due numeri complessi
$$ \alpha = \arctan \frac{3}{1} = 71.57° $$
$$ \beta = \arctan \frac{2}{4} = 26.57° $$
Pertanto, i due numeri complessi z1 e z2 in forma trigonometrica sono
$$ z_1 = 3.16 \cdot ( \cos 71.57° + i \cdot \sin 71.57° ) $$
$$ z_2 = 4.47 \cdot ( \cos 26.57° + i \cdot \sin 26.57° ) $$
Le coordinate polari [r,α] dei due numeri complessi z1 e z2 corrispondono agli stessi punti sul piano di Gauss.
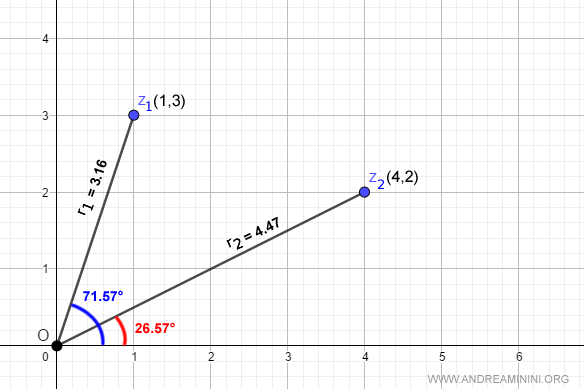
Una volta calcolate le coordinate polari [r,α] trasformo i due numeri complessi nella forma esponenziale usando la formula di Eulero z=reiα
$$ z_1 = 3.16 \cdot e^{i \cdot 71.57°} $$
$$ z_2 = 4.47 \cdot e^{i \cdot 26.57°} $$
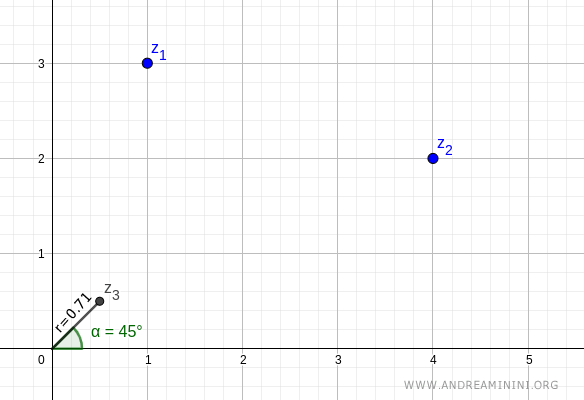
A questo punto calcolo la divisione dei due numeri complessi in forma esponenziale
$$ \frac{z_1}{z_2} = \frac{3.16}{4.47} \cdot e^{i \cdot (71.57°-26.57°)}$$
$$ z_1 \cdot z_2 = 0.71 \cdot e^{i \cdot (45°)}$$
Poi converto il quoziente in forma trigonometrica
$$ z_1 \cdot z_2 = 0.71 \cdot ( \cos 45° + i \cdot \sin 45° ) $$
Infine, lo converto in forma algebrica calcolando i valori del seno e del coseno
$$ z_1 \cdot z_2 = 0.71 \cdot \cos 45° + 0.71 \cdot i \cdot \sin 45° $$
$$ z_1 \cdot z_2 = 0.71 \cdot 0.71 + 0.71 \cdot i \cdot 0.71 $$
$$ z_1 \cdot z_2 = 0.5 + 0.5 i$$
Il risultato è il quoziente dei due numeri complessi.
Verifica. Per verificare se il risultato è corretto, calcolo la divisione dei due numeri complessi in forma algebrica. $$ \frac{z_1}{z_2} = \frac{1+3i}{4+2i} $$ $$ \frac{z_1}{z_2} = \frac{1+3i}{4+2i} \cdot \frac{4-2i}{4-2i} $$ $$ \frac{z_1}{z_2} = \frac{(1+3i) \cdot (4-2i)}{(4+2i) \cdot (4-2i) } $$ $$ \frac{z_1}{z_2} = \frac{4-2i+12i-6i^2}{16-8i+8i-4i^2} $$ $$ \frac{z_1}{z_2} = \frac{4+10i-6 \cdot (-1)}{16-4\cdot(-1)} $$ $$ \frac{z_1}{z_2} = \frac{10+10i}{20} $$ $$ \frac{z_1}{z_2} = \frac{1+i}{2} $$ $$ \frac{z_1}{z_2} = 0.5 + 0.5 i $$ Il risultato è lo stesso
E così via.
