Radice n-esima di un numero complesso

La radice ennesima $ \sqrt[n]{z} $ di un numero complesso $ z $ è ogni numero complesso $ w $ tale che $ w^n = z $ $$ w = \sqrt[n]{z} \Longleftrightarrow w^n = z $$

Per trovare le radici ennesime di un numero complesso $ z = a+bi $ devo considerare il numero nella forma trigonometrica.

$$ z = r \cdot ( cos \alpha + i \cdot \sin \alpha ) $$

Calcolo la radice del numero complesso con indice n.

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot [ \cos (\frac{\alpha}{n} + \frac{2k\pi}{n}) + i \cdot \sin (\frac{\alpha}{n} + \frac{2k\pi}{n}) ] $$

Svolgendo questo calcolo ottengo tutte le radici ennesime complesse del numero z.

Quante sono le radici ennesime di un numero complesso?

La radice ennesima di un numero complesso \( z \) ammette \( n \) soluzioni distinte, distribuite uniformemente sulla circonferenza di raggio \( \sqrt[n]{r} \) nel piano complesso.

Questo significa che formano i vertici di un poligono regolare con n lati inscritto nella circonferenza.

Tra queste, però, la radice principale è quella corrispondente a \( k = 0 \), ovvero l'angolo più piccolo positivo ottenuto dalla divisione di \( \alpha \) (l'argomento di \( z \)) per \( n \).

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot [ \cos (\frac{\alpha}{n}) + i \cdot \sin (\frac{\alpha}{n}) ] $$

Pertanto, quando si parla di "radice \( n \)-esima" in senso stretto, ci si riferisce solitamente alla radice principale, perché le altre radici \( n \)-esime distinte possono essere facilmente derivate dalla radice principale, aggiungendo multipli di \( \frac{2\pi}{n} \) all'angolo (argomento).

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot [ \cos (\frac{\alpha}{n} + \frac{2k\pi}{n}) + i \cdot \sin (\frac{\alpha}{n} + \frac{2k\pi}{n}) ] $$

Nota. In realtà, le radici ennesime di un numero complesso formano una successione infinita, se considero ogni ciclo della circonferenza complessa oltre il primo. Quindi le radici sono $$ \theta_k = \frac{\alpha}{n} + \frac{2k\pi}{n} + 2m\pi, \quad \text{con } k = 0, 1, \dots, n-1, \; m \in \mathbb{Z} $$ Formalmente sono infinite perché \( m \) può essere qualsiasi intero. In altre parole, a ogni \( k \), posso aggiungere \( 2\pi m \) (con \( m \in \mathbb{Z} \)) che mi riporta sempre al punto di partenza dopo tot giri. Tuttavia, è uso comune considerare solo le n radici distinte del primo giro (ciclo) della circonferenza ossia $ m = 0 $.

Un esempio pratico

Considero il numero complesso

$$ z = 16 \left(\cos \frac{3\pi}{4} + i \sin \frac{3\pi}{4}\right) $$

Devo trovare le radici quarte $ n = 4 $ del numero $ z $.

$$ \sqrt[4]{z} = \sqrt[4]{r} \cdot [ \cos (\frac{\alpha}{4} + \frac{2k\pi}{4}) + i \cdot \sin (\frac{\alpha}{4} + \frac{2k\pi}{4}) ] $$

In questo caso il modulo \( r \) di \( z \) è \( 16 \) mentre l'argomento \( \alpha \) è \( \frac{3\pi}{4} \).

$$ \sqrt[4]{z} = \sqrt[4]{16} \cdot [ \cos (\frac{ \frac{3\pi}{4} }{4} + \frac{2k\pi}{4}) + i \cdot \sin (\frac{  \frac{3\pi}{4} }{4} + \frac{2k\pi}{4}) ] $$

$$ \sqrt[4]{z} = 2 \cdot [ \cos ( \frac{3\pi}{4} \cdot \frac{1}{4} + \frac{2k\pi}{4}) + i \cdot \sin ( \frac{3\pi}{4} \cdot \frac{1}{4}  + \frac{2k\pi}{4}) ] $$

$$ \sqrt[4]{z} = 2 \cdot [ \cos ( \frac{3\pi}{16} + \frac{2k\pi}{4}) + i \cdot \sin ( \frac{3\pi}{16}  + \frac{2k\pi}{4}) ] $$

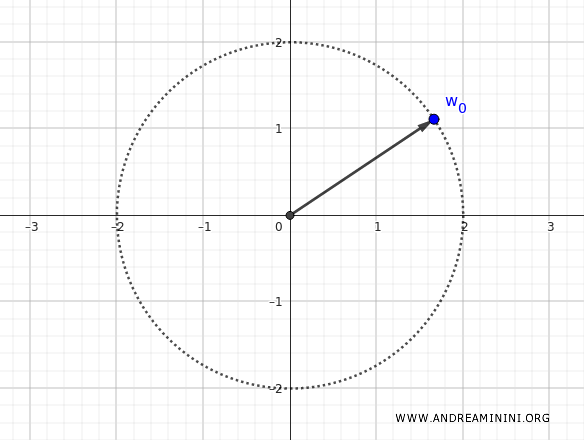
La radice principale con $ k=0 $ è:

$$ w_0 = 2 \left[\cos\left(\frac{3\pi}{16}\right) + i \sin\left(\frac{3\pi}{16}\right)\right] $$

Quindi, il numero complesso $ w_0 $ è la radice quarta principale del numero complesso $ z $.

Le altre radici (\( k = 1, 2, 3 \)) le ottengo aggiungendo i multipli di \( \frac{2\pi}{4} = \frac{\pi}{2} \) all'argomento.

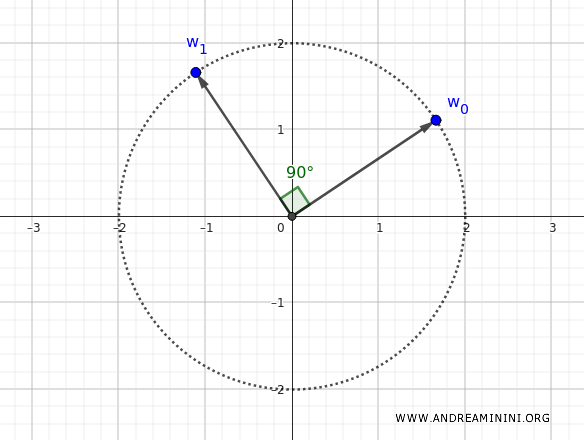
Ad esempio, la seconda radice (\( k = 1 \)) è:

$$ w_1 = 2 \left[\cos\left(\frac{3\pi}{16} + \frac{\pi}{2}\right) + i \sin\left(\frac{3\pi}{16} + \frac{\pi}{2}\right)\right] $$

Calcolo l'angolo: \( \frac{3\pi}{16} + \frac{\pi}{2} = \frac{3\pi}{16} + \frac{8\pi}{16} = \frac{11\pi}{16} \)

$$ w_1 = 2 \left[\cos\left(\frac{11\pi}{16}\right) + i \sin\left(\frac{11\pi}{16}\right)\right] $$

La seconda radice quarta $ w_1 $ si trova dopo un angolo di 90° rispetto alla prima perché con $n = 4 $ la circonferenza viene suddivisa in quattro parti uguali.

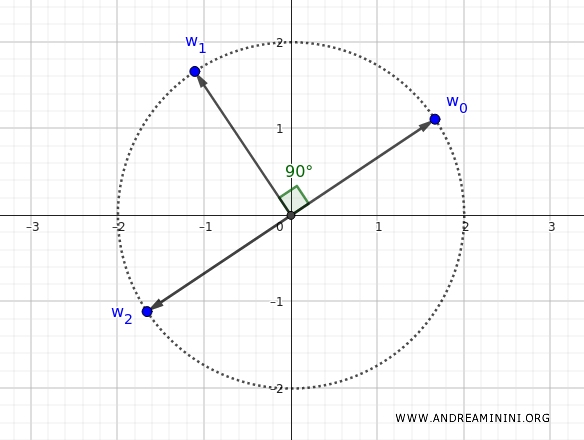
La terza radice (\( k = 2 \)) è:

$$ w_2 = 2 \left[\cos\left(\frac{3\pi}{16} + 2 \cdot \frac{\pi}{2}\right) + i \sin\left(\frac{3\pi}{16} + 2 \cdot \frac{\pi}{2}\right)\right] $$

Calcolo l'angolo: \( \frac{3\pi}{16} + \pi = \frac{3\pi}{16} + \frac{16\pi}{16} = \frac{19\pi}{16} \).

$$ w_2 = 2 \left[\cos\left(\frac{19\pi}{16}\right) + i \sin\left(\frac{19\pi}{16}\right)\right] $$

Ecco la rappresentazione del numero $ w_2 $ sul piano complesso.

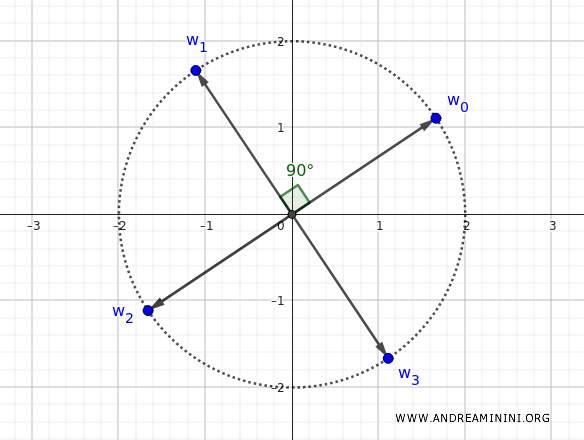
La quarta radice  (\( k = 3 \)) è:

$$ w_3 = 2 \left[\cos\left(\frac{3\pi}{16} + 3 \cdot \frac{\pi}{2}\right) + i \sin\left(\frac{3\pi}{16} + 3 \cdot \frac{\pi}{2}\right)\right] $$

Calcolo l'angolo: \( \frac{3\pi}{16} + \frac{3\pi}{2} = \frac{3\pi}{16} + \frac{24\pi}{16} = \frac{27\pi}{16} \).

$$ w_3 = 2 \left[\cos\left(\frac{27\pi}{16}\right) + i \sin\left(\frac{27\pi}{16}\right)\right] $$

La quarta radice $ w_3 $ del numero $ z $ completa la suddivisione della circonferenza in quattro parti uguali.

Nota. Come anticipato, l'ultima radice $ w_3 $ completa il primo "giro" della circonferenza. Nulla però vieta di farne altri, un secondo o un terzo giro, nello stesso verso o nel verso opposto ecc. Questo però porterebbe a individuare gli stessi punti della circonferenza già trovati. Pertanto, è sufficiente trovare le prime $ n=4 $ radici o, meglio ancora, individuare solo la radice principale $ w_0 $ e ricavare le altre soluzioni di conseguenza aggiungendo i multipli di un angolo che suddivide la circonferenza in n parti uguali (90° nel caso di una radice quarta $ \sqrt[4]{z} $).

Ricapitolando, le $ n = 4 $ radici quarte del numero complesso $ z $ sono:

$$ w_0  = 2 \left[\cos\left(\frac{3\pi}{16}\right) + i \sin\left(\frac{3\pi}{16}\right)\right] $$

$$ w_1  = 2 \left[\cos\left(\frac{11\pi}{16}\right) + i \sin\left(\frac{11\pi}{16}\right)\right] $$

$$ w_2  = 2 \left[\cos\left(\frac{19\pi}{16}\right) + i \sin\left(\frac{19\pi}{16}\right)\right] $$

$$ w_3  = 2 \left[\cos\left(\frac{27\pi}{16}\right) + i \sin\left(\frac{27\pi}{16}\right)\right] $$

Questi valori rappresentano le 4 radici equidistanti nel piano complesso.

La dimostrazione

Considero un numero complesso z

$$ z = r ( \cos \alpha + i \sin \alpha ) $$

Per ipotesi, il numero complesso w è la radice ennesima di z

$$ w = s ( \cos \beta + i \sin \beta ) $$

Essendo la radice ennesima di z, la potenza ennesima di w è uguale a z

$$ w^n = z $$

$$ w^n = r ( \cos \alpha + i \sin \alpha ) $$

$$ [s ( \cos \beta + i \sin \beta )]^n = r ( \cos \alpha + i \sin \alpha ) $$

Calcolo la potenza ennesima di $ w^n $ con la formula di De Moivre

$$ s^n ( \cos n\beta + i \sin n\beta ) = r ( \cos \alpha + i \sin \alpha ) $$

Ora confronto la parte sinistra con quella destra dell'equazione

$$ \color{red}{s^n} ( \cos \color{blue}{n\beta} + i \sin \color{blue}{n\beta} ) = \color{red}r ( \cos \color{blue}{\alpha} + i \sin \color{blue}{\alpha} ) $$

Dal confronto deduco che:

$$ \begin{cases} s^n = r \\ \\ n \beta = \alpha \end{cases} $$

Considero anche il fatto che $ n \beta $ è uguale agli angoli $ \alpha $ dopo uno o più angoli giro $ 2 \pi k = 360° \cdot k $

$$ \begin{cases} s^n = r \\ \\ n \beta = \alpha + 2 \pi k \end{cases} $$

Da questo deduco che $ \beta = \frac{\alpha}{n} + \frac{2\pi k}{n} $

$$ \begin{cases} s^n = r \\ \\ \beta = \frac{\alpha}{n} + \frac{2\pi k}{n} \end{cases} $$

Pertanto, posso affermare che le radici ennesime di z sono:

$$ \sqrt[n]{z} = \sqrt[n]{r ( \cos \alpha + i \sin \alpha)} $$

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \sqrt[n]{\cos \alpha + i \sin \alpha} $$

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \left( \cos \frac{\alpha}{n} + i \sin \frac{\alpha}{n} \right) $$

Considerando anche gli angoli giro diventa

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \left[ \cos ( \frac{\alpha}{n} + \frac{2\pi k}{n} ) + i \sin ( \frac{\alpha}{n} + \frac{2\pi k}{n}) \right] $$

Sapendo che $ s^n=r $ e $ \beta = \frac{\alpha}{n} + \frac{2\pi k}{n} $

$$ \sqrt[n]{z} = \sqrt[n]{s^n} \cdot \left[ \cos ( \beta ) + i \sin ( \beta ) \right] $$

$$ \sqrt[n]{z} = s \cdot \left[ \cos ( \beta ) + i \sin ( \beta ) \right] $$

$$ \sqrt[n]{z} =w $$

Questo conferma che $ w $ è la radice ennesima di $ z $.

La radice quadrata dei numeri negativi

Questo approccio mi permette anche di spiegare la radice dei numeri negativi.

Ad esempio, calcolo la radice quadrata di \(-4\) usando il metodo basato sulla forma trigonometrica.

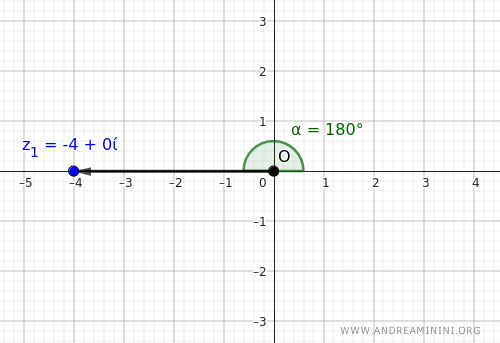
Per prima cosa, scrivo il numero complesso \(z=-4\) in forma trigonometrica:

• Il modulo di \(-4\) è: $$ r = \lvert -4 \rvert = 4 $$
• L'argomento \(\alpha\) (l'angolo che il numero forma con l'asse reale positivo) è: $$ \alpha = \pi \quad \text{(angolo di 180° perché \(-4\) è sul semiasse reale negativo)} $$

Quindi, posso scrivere il numero complesso -4 in questa forma:

$$ -4 = 4 \cdot \left(\cos\pi + i\sin\pi\right) $$

Applico la formula per la radice quadrata (\(n = 2\)):

$$ \sqrt[2]{z} = \sqrt[2]{r} \cdot \left[\cos\left(\frac{\alpha}{2} + k\frac{2\pi}{2}\right) + i\sin\left(\frac{\alpha}{2} + k\frac{2\pi}{2}\right)\right], \quad k = 0, 1 $$

$$ \sqrt[2]{z} = \sqrt[2]{r} \cdot \left[\cos\left(\frac{\alpha}{2} + k \pi \right) + i\sin\left(\frac{\alpha}{2} + k \pi \right)\right], \quad k = 0, 1 $$

In questo caso \( r = 4 \) e  \(\alpha = \pi\).

$$ \sqrt[2]{-4} = \sqrt[2]{4} \cdot \left[\cos\left(\frac{\pi}{2} + k \pi \right) + i\sin\left(\frac{\pi}{2} + k \pi \right)\right], \quad k = 0, 1 $$

$$ \sqrt[2]{-4} = 2 \cdot \left[\cos\left(\frac{\pi}{2} + k \pi \right) + i\sin\left(\frac{\pi}{2} + k \pi \right)\right], \quad k = 0, 1 $$

Calcolo le due radici:

1. Per \(k = 0\): $$ w_0 = 2 \cdot \left[\cos\left(\frac{\pi}{2}\right) + i\sin\left(\frac{\pi}{2}\right)\right] $$ Semplificando: $$
   w_0 = 2 \cdot \left[0 + i\cdot 1\right] $$ $$ w_0= 2i $$
2. Per \(k = 1\): $$ w_1 = 2 \cdot \left[\cos\left(\frac{\pi}{2} + \pi\right) + i\sin\left(\frac{\pi}{2} + \pi\right)\right]. $$ Semplificando: $$ w_1 = 2 \cdot \left[\cos\left(\frac{3\pi}{2}\right) + i\sin\left(\frac{3\pi}{2}\right)\right] $$ Poiché \(\cos\left(\frac{3\pi}{2}\right) = 0\) e \(\sin\left(\frac{3\pi}{2}\right) = -1\), otteniamo: $$ w_1 = 2 \cdot \left[0 - i\cdot 1\right] $$ $$ w_1 = -2i $$

Quindi, le radici quadrate di \(-4\) sono:

$$ w_0 = 2i \quad \text{e} \quad w_1 = -2i $$

La radice principale di \(-4\) è \( w_0 = 2i \), mentre l'altra radice è \( w_1 = -2i \).

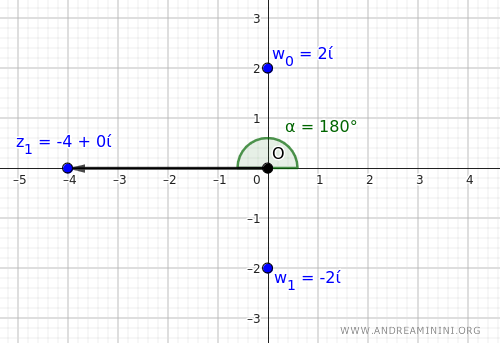
Questi sono i due numeri complessi che, elevati al quadrato, restituiscono \(-4\).

E così via.