La divisione tra numeri complessi in forma trigonometrica

Dati due numeri in forma trigonometrica $$ z = d \cdot ( \cos a + i \cdot \sin a ) \\ z' = d' \cdot ( \cos a' + i \cdot \sin a' ) $$ la divisione tra i due numeri si ottiene con la seguente formula $$ \frac{z}{z'} = \frac{d}{d'} \cdot [ \cos (a-a') + i \cdot \sin (a-a') ] $$

Un esempio pratico

Prendo in considerazione due numeri complessi

$$ z=1+3i $$

$$ z'=4+2i $$

Li divido usando la formula

$$ \frac{x+iy}{x'+iy'} = \frac{xx'+yy'}{x'^2+y'^2}+i \cdot \frac{x'y-xy'}{x'^2+y'^2} $$

$$ \frac{z}{z'} = \frac{1+i3}{4+i2} = \frac{1·4+3·2}{4^2+2^2}+i \cdot \frac{4·3-1·2}{4^2+2^2} $$

$$ \frac{4+6}{16+4}+i \cdot \frac{12-2}{16+4} $$

$$ \frac{10}{20}+i \cdot \frac{10}{20} $$

$$ \frac{1}{2}+i \cdot \frac{1}{2} $$

Provo a rifare il calcolo con i numeri in forma trigonometrica

$$ z = 3.16 \cdot ( \cos 71.57° + i \cdot \sin 71.57° ) $$

$$ z' = 4.47 \cdot ( \cos 26.57° + i \cdot \sin 26.57° ) $$

Spiegazione. Gli angoli sono misurati in gradi mentre i valori d e d' indicano la lunghezza di ciascun segmento.

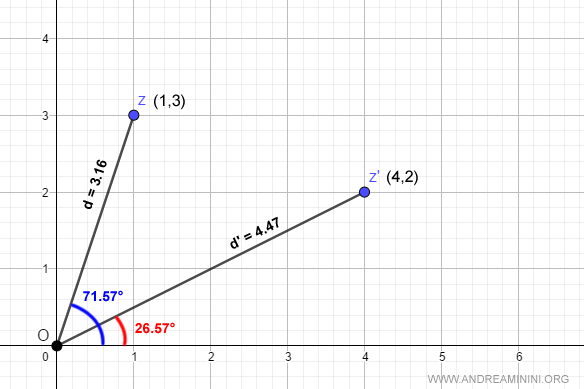
La lunghezza dei segmenti d e d' è approssimata per semplificare i calcoli. $$ d = \sqrt{1^2+3^2}=\sqrt{10} ≅ 3.16 \\ d' = \sqrt{4^2+2^2}=\sqrt{20}≅ 4.47 $$

A questo punto uso la formula della divisione tra numeri complessi in forma trigonometrica

$$ \frac{z}{z'} = \frac{d}{d'} \cdot [ \cos (a-a') + i \cdot \sin (a-a') ] $$

$$ \frac{3.16}{4.47} \cdot [ \cos (71.57°-26.57°) + i \cdot \sin (71.57°-26.57°) ] = $$

$$ 0.706 \cdot [ \cos (45°) + i \cdot \sin (45°) ] = $$

$$ 0.706 \cdot [ 0.70710678118 + i \cdot 0.70710678118 ] = $$

$$ 0.5 + i \cdot 0.5 $$

Il risultato è lo stesso.

La dimostrazione

Prendo in considerazione due numeri complessi rappresentati in forma trigonometrica.

$$ z = d \cdot ( \cos a + i \cdot \sin a ) \\ z' = d' \cdot ( \cos a' + i \cdot \sin a' ) $$

La divisione algebrica è

$$ \frac{z}{z'} = \frac{ d \cdot ( \cos a + i \cdot \sin a ) }{ d' \cdot ( \cos a' + i \cdot \sin a' } $$

Moltiplico numeratore e denominatore per lo stesso fattore, ossia per il numero complesso coniugato del denominatore.

$$ \frac{z}{z'} = \frac{ d \cdot ( \cos a + i \cdot \sin a ) }{ d' \cdot ( \cos a' + i \cdot \sin a' ) } \cdot \frac{ d' \cdot ( \cos a' - i \cdot \sin a' ) }{ d' \cdot ( \cos a' - i \cdot \sin a' ) } = $$

Semplifico

$$ \frac{ d \cdot ( \cos a + i \cdot \sin a ) }{ d' \cdot ( \cos a' + i \cdot \sin a' ) } \cdot \frac{ ( \cos a' - i \cdot \sin a' ) }{ ( \cos a' - i \cdot \sin a' ) } = $$

$$ \frac{d}{d'} \cdot \frac{ ( \cos a \cdot (\cos a') + \cos a \cdot ( - i \cdot \sin a') + i \cdot \sin a \cdot (\cos a') + i \cdot \sin a \cdot ( - i \cdot \sin a') ) }{ ( \cos a' \cdot ( \cos a' ) + \cos a' \cdot ( - i \cdot \sin a' ) + i \cdot \sin a' \cdot ( \cos a' ) + i \cdot \sin a' \cdot ( - i \cdot \sin a' ) ) } = $$

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' - i^2 \cdot \sin a \cdot \sin a' }{ \cos^2 a' - \cos a' \cdot i \cdot \sin a' + i \cdot \sin a' \cdot \cos a' - i^2 \cdot \sin^2 a' } = $$

Poiché l'unità immaginaria i²=-1

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' - (-1) \cdot \sin a \cdot \sin a' }{ \cos^2 a' - \cos a' \cdot i \cdot \sin a' + i \cdot \sin a' \cdot \cos a' - (-1) \cdot \sin^2 a' } = $$

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' + \sin a \cdot \sin a' }{ \cos^2 a' - \cos a' \cdot i \cdot \sin a' + i \cdot \sin a' \cdot \cos a' + \sin^2 a' } = $$

Due termini al denominatore si annullano tra loro

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' + \sin a \cdot \sin a' }{ \cos^2 a' + \sin^2 a' } = $$

Sapendo che cos² x+sin² x=1

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' + \sin a \cdot \sin a' }{ 1 } = $$

$$ \frac{d}{d'} \cdot [ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' + \sin a \cdot \sin a' ] = $$

Nota. Sapendo che in trigonometria secondo le formule di addizione e sottrazione la somma degli angoli è $$ \sin (A+B) = \sin A \cos B + \cos A \sin B $$ $$ \sin (A-B) = \sin A \cos B - \cos A \sin B $$ $$ \cos(A+B) = \cos A \cos B - \sin A \sin B $$ $$ \cos(A-B) = \cos A \cos B + \sin A \sin B $$

$$ \frac{d}{d'} \cdot [ ( \cos a \cdot \cos a' + \sin a \cdot \sin a' ) + i \cdot ( \sin a \cdot \cos a' - \cos a \cdot \sin a' ) ] = $$

$$ \frac{d}{d'} \cdot [ \cos (a-a') + i \cdot \sin a-a' ] = $$

E così via.