Rappresentazione dei numeri complessi
La rappresentazione cartesiana
I numeri complessi possono essere rappresentati sotto forma di coordinate (x,y) del piano cartesiano. $$ x+yi \equiv P(x,y) $$
Un esempio pratico
Prendo in considerazione il numero complesso
$$ 3+2i $$
Dove x=3 e y=2 mentre i è l'unità immaginaria.
Posso rappresentare questo numero come un punto P di coordinate (x,y) sul piano cartesiano a due dimensioni.
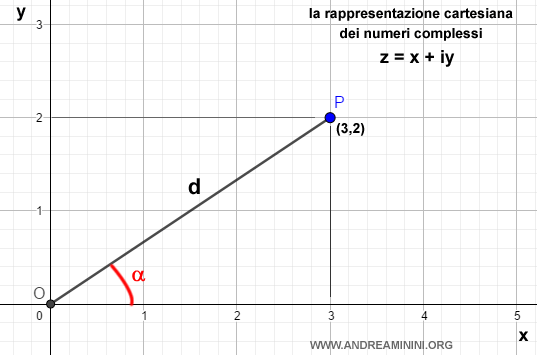
L'interpretazione geometrica
Dal punto di vista geometrico ogni numero complesso può essere identificato anche da una coppia di valori
- il modulo ossia la lunghezza d del segmento OP
- l'angolo (fase o argomento) del segmento OP misurato in gradi o radianti. E' anche detta fase o argomento.
Per misurare la lunghezza del segmento OP, ossia la distanza tra il punto P(x,y) e l'origine O del piano cartesiano, uso il teorema di Pitagora.
$$ d = \sqrt{x^2+y^2} $$
L'angolo è invece determinato dalle seguenti formule
$$ \cos α = \frac{x}{d} $$ $$ \sin α = \frac{y}{d} $$
Dimostrazione. La proiezione sull'asse orizzontale x è $$ x = d \cdot \cos \alpha $$ metto in evidenza il coseno è ottengo $$ \cos \alpha = \frac{x}{d} $$ La proiezione sull'asse verticale y è $$ y = d \cdot \sin \alpha $$ Metto in evidenza il seno e ottengo $$ \sin \alpha = \frac{y}{d} $$
Un esempio pratico
Prendo in considerazione il numero complesso
$$ 3+2i $$
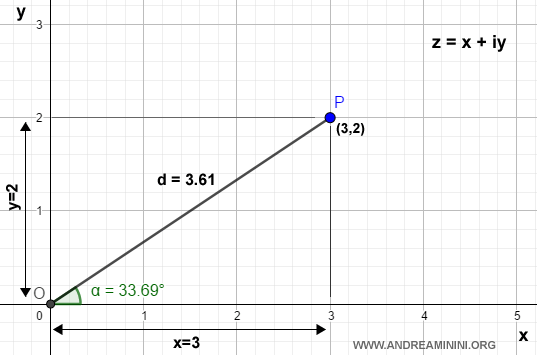
So già che individua il punto P alle coordinate (3,2) del piano cartesiano.

La lunghezza (d) del segmento OP
$$ d = \sqrt{3^2 + 2^2} $$
$$ d = \sqrt{9 + 4} = \sqrt{13} = 3.61 $$
Per trovare l'angolo calcolo il rapporto tra x e d.
$$ \cos α = \frac{x}{d} $$
$$ \cos α = \frac{3}{3.61} = 0.83 $$
Ho trovato il coseno dell'angolo α
$$ \cos α = 0.83 $$
Per conoscere l'angolo in gradi o radianti calcolo l'arcocoseno
$$ \arccos 0.83 = 33.69° $$
Quindi l'angolo misura 33.69°
Nota. Avrei potuto calcolare l'angolo anche usando l'altra formula $$ \sin α = \frac{y}{d} $$ tramite l'arcoseno.
Questo mi dà la possibilità di rappresentare un numero complesso anche in una forma trigonometrica.
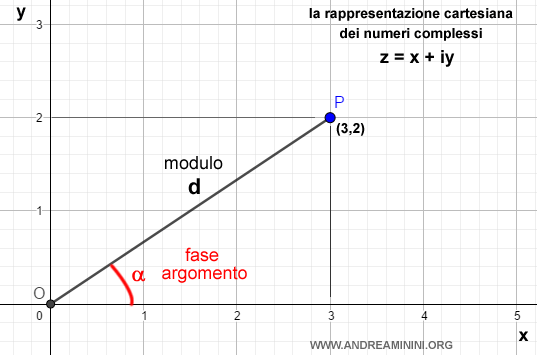
La rappresentazione trigonometrica ( o polare )
I numeri complessi possono essere rappresentati in forma trigonometrica o polare. $$ x+yi \equiv d ( \cos α + i \cdot \sin α ) $$
E' detta polare perché si basa sulle coordinate polari
$$ ( d, a ) $$
ossia dal modulo (d) del segmento che congiunge l'origine con il punto P e dall'angolo (a) anche detto fase o argomento.
Dimostrazione
Un generico numero complesso
$$ z = x+yi $$
Sapendo che
$$ x = d \cdot \cos α $$
$$ y = d \cdot \sin α $$
Posso riscrivere il numero complesso nella forma
$$ z = d \cdot \cos α + i \cdot ( d \cdot \sin α ) $$
$$ z = d ( \cos α + i \cdot \sin α ) $$
Verifica. Nell'esempio precedente il modulo è lungo d=3.61, il coseno è 0.83 e il seno è 0.55 $$ d=3.61 \\ \cos α = 0.83 \\ \sin α = 0.55 $$ Pertanto, i valori x e y sono $$ x = d \cdot \cos α = 3.61 \cdot 0.83 = 3 $$ $$ y = d \cdot \sin α = 3.61 \cdot 0.55 = 2 $$ I conti tornano.
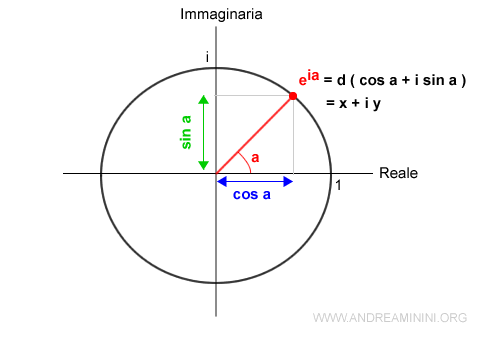
La rappresentazione esponenziale
Un numero complesso può essere rappresentato anche in forma esponenziale. $$ z = d \cdot (\cos α + i \cdot \sin α ) = d \cdot e^{i \cdot α} $$ con α∈(0,2π).
Questa notazione è detta rappresentazione esponenziale.
Si ottiene utilizzando la formula di Eulero secondo la quale
$$ d ( \cos a + i \cdot \sin a) = d \cdot e^{i \cdot a} $$
La formula di Eulero permette di usare la funzione esponenziale per rappresentare le funzioni trigonometriche.
Nota. Il numero complesso coniugato (x-iy) del numero z=x+iy nella forma esponenziale è $$ d \cdot (\cos a - i \cdot \sin a ) = d \cdot e^{-i \cdot a} $$
Un esempio
Il numero complesso in forma trigonometrica (polare)
$$ z = 3.61 \cdot ( \cos 33.69° + i \cdot \sin 33.69° ) $$
posso scriverlo nella forma esponenziale equivalente
$$ z = 3.61 \cdot e ^ {i \cdot 33.69° } $$
Perché usare la forma esponenziale dei numeri complessi? In genere la forma esponenziale si utilizza quando il modulo e la fase del numero complesso hanno maggiore importanza rispetto alla parte reale e immaginaria del numero. Se conosco il modulo e la fase posso svolgere tutte le operazioni matematiche più rapidamente
E così via.
