La radice di un numero complesso
Per calcolare la radice n-sima n√z di un numero complesso z=a+bi, dove n è un numero intero positivo, lo converto in forma trigonometrica $$ z = d \cdot [ \cos a + i \cdot \sin a ] $$ poi calcolo la radice con la seguente formula $$ \sqrt[n]{z} = \sqrt[n]{d} \cdot [ \cos \frac{(a+2πk)}{n} + i \cdot \sin \frac{(a+2πk) }{n} ] $$ per ogni k da 0 a n-1.
La radice n-esima di z è un numero complesso w tale che la sua potenza n-esima è a z
$$ \sqrt[n]{z} = w \Leftrightarrow w^n = z $$
Ogni numero complesso z diverso da zero ha n radici n-esime.
Quindi, la radice quadrata ammette due radici, la radice cubica tre radici, ecc.
La radice n-esima di un numero complesso in forma esponenziale
In alternativa, posso calcolare la radice n-esima di un numero complesso anche in forma esponenziale.
Nella forma esponenziale la radice n-esima n√z di un numero complesso è la seguente $$ \sqrt[n]{z} = d^{\frac{1}{n}} \cdot e^{i \cdot \frac{(a+2πk)}{n} } $$ o più in generale $$ \sqrt[n]{z^m} = d^{\frac{m}{n}} \cdot e^{i \cdot m \cdot \frac{(a+2πk)}{n} } $$ dove n è un numero intero positivo (n>0).
Un esempio pratico
Esempio 1
Prendo in considerazione il numero complesso
$$ z = 3 + i 2 $$
Dal punto di vista grafico il numero z individua il punto P di coordinate (3,2) sul punto.
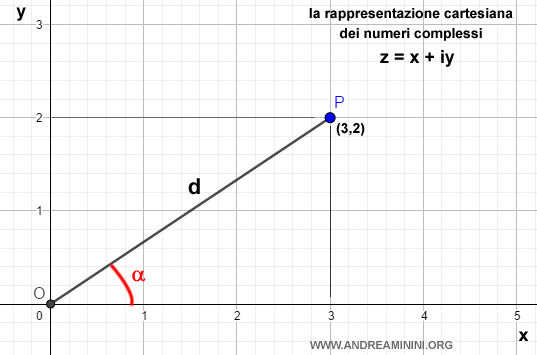
Il numero z nella forma trigonometrica è
$$ z = d ( \cos a + i \cdot \sin a ) $$
Calcolo il modulo d
$$ z = \sqrt{3^2+2^2} ( \cos a + i \cdot \sin a ) $$
$$ z = \sqrt{13} ( \cos a + i \cdot \sin a ) $$
Sapendo che
$$ \cos a = \frac{x}{d} = \frac{3}{\sqrt{13}} $$
$$ \sin a = \frac{y}{d} = \frac{2}{\sqrt{13}} $$
Per trovare l'angolo uso l'arcocoseno o l'arcoseno
$$ a= \arccos ( \cos a ) = \arccos ( \frac{3}{\sqrt{13}} ) = 0.5880026035475675 rad $$
$$ a= \arcsin ( \sin a ) = \arcsin ( \frac{2}{\sqrt{13}} ) = 0.5880026035475675 rad $$
Quindi, semplificando il numero complesso in forma trigonometrica è
$$ z = \sqrt{13} ( \cos a + i \cdot \sin a ) $$
La sua radice quadrata (n=2) è
$$ \sqrt[n]{z} = \sqrt[n]{d} \cdot [ \cos \frac{(a+2πk)}{n} + i \cdot \sin \frac{ (a+2πk) }{n} ] $$
$$ \sqrt[2]{ \sqrt{13} } \cdot [ \cos \frac{ (a+2πk)}{2} + i \cdot \sin \frac{ (a+2πk) }{2} ] $$
Con a= 0.5880026035475675 radianti.
Essendo una radice quadrata ha n=2 soluzioni ossia k=0 e k=1
Per k=0
$$ \sqrt[2]{ \sqrt{13} } \cdot [ \cos \frac{ 0.5880026035475675}{2} + i \cdot \sin \frac{ 0.5880026035475675 }{2} ] $$
$$ = 1.817 + i \cdot 0.55 $$
Per k=1
$$ \sqrt[2]{ \sqrt{13} } \cdot [ \cos \frac{ (0.5880026035475675+2π)}{2} + i \cdot \sin \frac{ (0.5880026035475675+2π) }{2} ] $$
$$ = -1.817 - i \cdot 0.55 $$
Esempio 2
Prendo in considerazione il numero complesso
$$ z = 0 + i 1 $$
ossia
$$ z = i $$
Nella rappresentazione trigonometrica è
$$ z = \sqrt{0^2+1^2} \cdot [ \cos \frac{π}{2} + i \cdot \sin \frac{π}{2} ] $$
$$ z = 1 \cdot [ \cos \frac{π}{2} + i \cdot \sin \frac{π}{2} ] $$
La sua radice quadrata ha due radici
Per k=0 è
$$ \sqrt{z} = \sqrt{0^2+1^2} \cdot [ \cos \frac{ \frac{π}{2} }{ 2} + i \cdot \sin \frac{ \frac{π}{2} }{2} ] $$
$$ \sqrt{1} \cdot [ \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} ] $$
$$ 1 \cdot [ \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} ] $$
$$ \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} $$
Per k=1 è
$$ \sqrt{z} = \sqrt{0^2+1^2} \cdot [ \cos \frac{ \frac{π}{2} +2π }{ 2} + i \cdot \sin \frac{ \frac{π}{2} +2π }{2} ] $$
$$ \sqrt{1} \cdot [ \cos \frac{5π}{4} + i \cdot \sin \frac{5π}{4} ] $$
$$ 1 \cdot [ \cos \frac{5π}{4} + i \cdot \sin \frac{5π}{4} ] $$
$$ \cos \frac{5π}{4} + i \cdot \sin \frac{5π}{4} $$
La dimostrazione
Dato un numero complesso
$$ z=x+iy $$
lo rappresento in forma trigonometrica
$$ z = d \cdot [ \cos a + i \cdot \sin a ] $$
se la sua radice quadrata è z'
$$ z' = d' \cdot [ \cos a' + i \cdot \sin a' ] $$
allora la potenza n-esima di z' è il numero z
$$ (z')^n = z $$
$$ (d' \cdot [ \cos a' + i \cdot \sin a' ])^n = z $$
$$ (d')^n \cdot ([ \cos a' + i \cdot \sin a' ])^n = d \cdot [ \cos a + i \cdot \sin a ] $$
Quindi d' deve essere necessariamente la radice n-esima di d
$$ d' = \sqrt[n]{d} $$
Pertanto
$$ \sqrt[n]{d} \cdot ([ \cos a' + i \cdot \sin a' ])^n = d \cdot [ \cos a + i \cdot \sin a ] $$
Poiché cos(a) si ripete ogni 360°=2π per k volte e lo stesso vale per sin(a)
$$ \sqrt[n]{d} \cdot ([ \cos a' + i \cdot \sin a' ])^n = d \cdot [ \cos (a+2πk) + i \cdot \sin (a+2πk) ] $$
Infine, applico al primo membro dell'equazione la formula di De Moivre sulle potenze dei numeri complessi .
$$ \sqrt[n]{d} \cdot [ \cos (n \cdot a') + i \cdot \sin (n \cdot a') ] = d \cdot [ \cos (a+2πk) + i \cdot \sin (a+2πk) ] $$
Spiegazione. Ad esempio, se n=2 ho $$ [ \cos a + i \cdot \sin a ]^2 $$ svolgo il quadrato del binomio e ottengo $$ \cos^2 a + 2 \cdot i \cdot \cos a \cdot \sin a + i^2 \cdot \sin^2 a $$ poiché l'unità immaginaria i2=-1 $$ \cos^2 a + 2 \cdot i \cdot \cos a \cdot \sin a + (-1) \cdot \sin^2 a $$ $$ \cos^2 a + 2 \cdot i \cdot \cos a \cdot \sin a - \sin^2 $$ Secondo le formule trigonometriche di duplicazione $$ \cos^2 A - \sin^2 A = \cos 2A \\ 2 \sin A \cos A = \sin 2A $$ Pertanto $$ ( \cos^2 a - \sin^2 a) + i \cdot ( 2 \cdot \cos a \cdot \sin a ) $$ $$ ( \cos 2a ) + i \cdot ( \sin 2a ) $$
Da questo deduco per confronto tra i due membri dell'equazione che vale la seguente uguaglianza
$$ (n \cdot a') = (a+2πk) $$
Pertanto l'angolo a' è uguale a
$$ a' = \frac{a+2πk}{n} $$
In conclusione, dato un numero complesso z qualsiasi
$$ z = d \cdot [ \cos a + i \cdot \sin a ] $$
se z' è la radice quadrata di z
$$ z' = \sqrt[n]{z} $$
$$ d' \cdot [ \cos a' + i \cdot \sin a' ] = \sqrt[n]{z} $$
Sostituisco d' e a' con le forme equivalenti che ho appena trovato
$$ \sqrt[n]{d} \cdot [ \cos \frac{a+2πk}{n} + i \cdot \sin \frac{a+2πk}{n} ] = \sqrt[n]{z} $$
Il risultato finale è la formula che volevo dimostrare.
Un metodo di calcolo alternativo
Una volta calcolata la prima radice n-esima di un numero complesso, posso calcolare le altre soluzioni della radice tramite il prodotto della prima soluzione per le radici ennesime dell'unità.
$$ \sqrt[n]{d} \cdot ( \cos \frac{\alpha}{n} + i \sin ) \frac{\alpha}{n} \cdot \sqrt[n]{1} $$
$$ \sqrt[n]{d} \cdot ( \cos \frac{\alpha}{n} + i \sin ) \frac{\alpha}{n} \cdot ( \cos \frac{2k\pi}{n} + i \sin \frac{2k\pi}{n} ) $$
Nota. La radice ennesima dell'unità è $$ \sqrt[n]{1} = \cos \frac{2k\pi}{n} + i \sin \frac{2k\pi}{n} $$ Dove k=0,1,...,n-1
Un esempio pratico
Considero il numero complesso che già studiato nell'esempio precedente
$$ 0+i $$
che in forma trigonometrica diventa
$$ z = 1 \cdot [ \cos \frac{\pi}{2} + i \cdot \sin \frac{\pi}{2} ] $$
La sua radice quadrata ha due radici
La prima radice per k=0 è
$$ \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} $$
Nota. Il calcolo l'ho già fatto nell'esempio precedente. Lo riporto qui come promemoria. Per k=0 la prima radice è $$ \sqrt{z} = \sqrt{0^2+1^2} \cdot [ \cos \frac{ \frac{π}{2} }{ 2} + i \cdot \sin \frac{ \frac{π}{2} }{2} ] $$ $$ \sqrt{1} \cdot [ \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} ] $$ $$ 1 \cdot [ \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} ] $$ $$ \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} $$
Per calcolare la seconda radice, anziché ripetere il calcolo con k=1, moltiplico la prima radice per la radice quadrata dell'unità
$$ ( \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} ) \cdot ( \cos \frac{2k \pi}{n} + i \cdot \sin \frac{2k \pi }{n} ) $$
$$ ( \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} ) \cdot ( \cos \frac{2 \cdot 1 \cdot \pi}{n} + i \cdot \sin \frac{2 \cdot 1 \cdot \pi }{n} ) $$
$$ ( \cos \frac{π}{4} + i \cdot \sin \frac{π}{4} ) \cdot ( \cos \frac{2 \pi}{n} + i \cdot \sin \frac{2 \pi }{n} ) $$
Calcolo il prodotto tra due numeri complessi in forma trigonometrica
$$ \cos ( \frac{π}{4} + \frac{2 \pi}{n} ) + i \cdot \sin ( \frac{π}{4} + \frac{2 \pi }{n} ) $$
Sapendo che n=2 ossia la radice quadrata ha due soluzioni
$$ \cos ( \frac{π}{4} + \frac{2 \pi}{2} ) + i \cdot \sin ( \frac{π}{4} + \frac{2 \pi }{2} ) $$
$$ \cos ( \frac{π+4 \pi}{4} ) + i \cdot \sin ( \frac{π+4\pi}{4} ) $$
$$ \cos ( \frac{5 \pi}{4} ) + i \cdot \sin ( \frac{5 \pi}{4} ) $$
Il risultato è uguale a quello già ottenuto nell'esempio precedente.
Verifica. Nell'esempio precedente ho calcolato la seconda radice per k=1 in questo modo $$ \sqrt{z} = \sqrt{0^2+1^2} \cdot [ \cos \frac{ \frac{π}{2} +2π }{ 2} + i \cdot \sin \frac{ \frac{π}{2} +2π }{2} ] $$ $$ \sqrt{1} \cdot [ \cos \frac{5π}{4} + i \cdot \sin \frac{5π}{4} ] $$ $$ 1 \cdot [ \cos \frac{5π}{4} + i \cdot \sin \frac{5π}{4} ] $$ $$ \cos \frac{5π}{4} + i \cdot \sin \frac{5π}{4} $$ Il risultato finale è sempre lo stesso.
E così via.
