Come confrontare i numeri complessi

Due numeri complessi sono uguali $$ z_1 = z_2 $$ se hanno la stessa parte reale e la stessa parte immaginaria. $$ Re(z_1) = Re(z_2) $$ $$ Im(z_1) = Im(z_2) $$

Nei numeri complessi è definita solo la relazione di equivalenza (uguaglianza).

Non è definita la relazione d'ordine.

Quindi, non posso dire se un numero complesso è maggiore o minore di un altro.

Esempio

Considero due numeri complessi

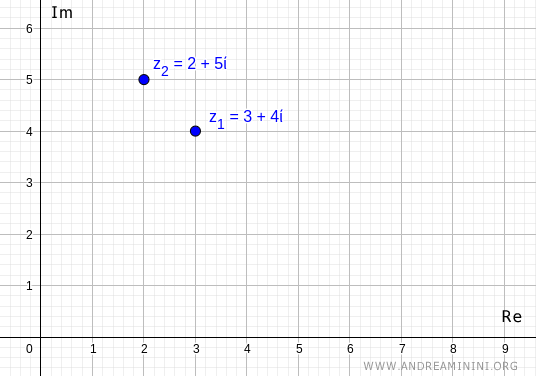
$$ z_1 = (3,4) $$

$$ z_2 = (2,5) $$

I due numeri non sono uguali

$$ z_1 \ne z_2 $$

perché la parte reale e immaginaria sono diverse

$$ Re(z_1) = 3 \ne Re(z_2) = 2 $$

$$ Im(z_1) = 4 \ne Im(z_2) = 5 $$

Non essendoci una relazione d'ordine, non posso dire se un numero complesso è maggiore dell'altro.

Esempio 2

Considero due numeri complessi

$$ z_1 = (2,3) $$

$$ z_2 = (2,3) $$

I due numeri complessi sono uguali perché sia la parte reale che la parte immaginaria sono uguali

$$ Re(z_1) = Re(z_2) = 2 $$

$$ Im(z_1) = Im(z_2) = 3 $$

I due numeri corrispondono allo stesso punto di coordinate (2,3) sul piano di Gauss.

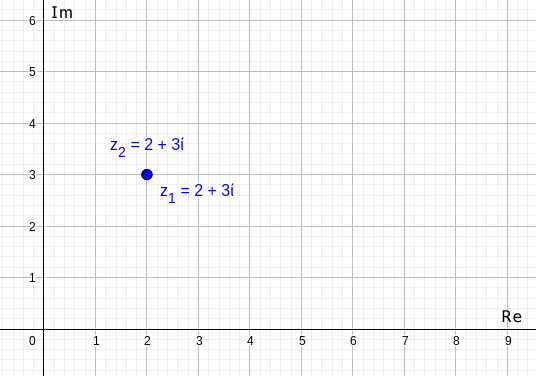
E così via.