Le formule di Eulero
La formula di Eulero è una relazione tra le funzioni trigonometriche seno e coseno e la funzione esponenziale complessa. $$ e^{ix} = \cos x + i \cdot \sin x $$ dove "x" è un numero reale (radianti), "e" è la base dei logaritmi naturali ed "i" è l'unità immaginaria dei numeri complessi.
A cosa serve?
La formula di Eulero permette di scrivere i numeri complessi in forma esponenziale.
$$ z = d \cdot e^{ix} = d \cdot ( \cos x + i \sin x ) $$
Dove d è il modulo e x è l'argomento del numero complesso ed è misurato in radianti.
Questo mi permette di usare la funzione esponenziale $ e^x $ al posto delle funzioni goniometriche.
In questa forma molte operazioni matematiche tra i numeri complessi diventano più semplici.
Ad esempio, la moltiplicazione tra due numeri complessi in forma esponenziale si calcola usando la proprietà delle potenze. $$ z_1 \cdot z_2 = ( r_1 \cdot e^{i \alpha } ) \cdot ( r_2 \cdot e^{i \beta} ) = ( r_1 \cdot r_2 ) \cdot e^{i(\alpha+\beta)} $$ Lo stesso accade per calcolare la divisione tra due numeri complessi. $$ \frac{z_1}{z_2} = \frac{r_1 \cdot e^{i \alpha }}{r_2 \cdot e^{i \beta}} = ( \frac{r_1}{r_2} ) \cdot e^{i(\alpha-\beta)} $$
Dalla prima formula di Eulero derivano altre tre formule molto utili nel calcolo scientifico.
Il numero complesso coniugato
$$ e^{-ix} = \cos x - i \cdot \sin x $$
Il coseno
$$ \cos x = \frac{e^{ix}+e^{-ix}}{2} $$
Il seno
$$ \sin x = \frac{e^{ix}-e^{-ix}}{2i} $$
Queste quattro formule sono dette formule di Eulero.
Esempio. Il numero complesso $$ z = 1+3i $$ in forma esponenziale si scrive $$ z = \sqrt{10} \cdot e^{i \cdot 71.57°} $$ Dove d=√10 è il modulo e x=71.57° è l'argomento. Per ottenere il numero complesso coniugato z'=1-3i in forma esponenziale basta cambiare il segno all'esponente. $$ z' = \sqrt{10} \cdot e^{-i \cdot 71.57°} $$ Una volta noti z e z' le altre formule di Eulero mi permettono di calcolare rapidamente il coseno e il seno dell'argomento x.
La spiegazione
Il valore x è l'angolo di un segmento che collega l'origine del piano complesso a un punto in una circonferenza con raggio unitario.
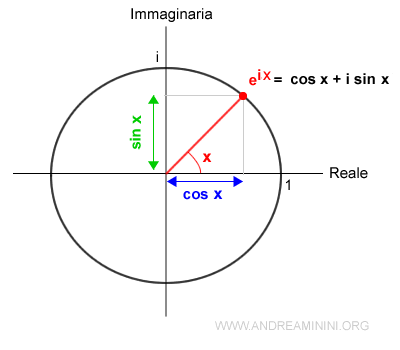
La lunghezza del segmento è il modulo del numero complesso mentre l'angolo di ampiezza x rispetto al semiasse positivo è l'argomento del numero complesso.
Il modulo e l'argomento [d;x] fomano le coordinate polari del numero complesso.
Sono le stesse coordinate polari del numero complesso in forma trigonometrica.
$$ d \cdot e^{ix} = d \cdot ( \cos x + i \cdot \sin x ) $$
Quindi, la formula di Eulero mi consente di rappresentare un numero complesso in forma esponenziale.
La dimostrazione
Dalla formula di Eulero ne derivano altre molto utili nel calcolo scientifico.
Il numero complesso coniugato
Il numero complesso coniugato del numero z=eix si ottiene cambiando il segno dell'esponente
$$ e^{-ix} = \cos x - i \cdot \sin x $$
Dimostrazione. Ho il numero complesso in forma algebrica, trigonometrica ed esponenziale $$ z = a+bi = d ( \cos x + i \sin x ) = d \cdot e^{ix} $$ Il coniugato del numero complesso in forma trigonometrica ha lo stesso modulo e argomento ma il segno della parte immaginaria è opposto (-i) $$z' = a-bi = d ( \cos x - i \sin x ) $$ Quindi per scrivere il coniugato in forma esponenziale basta cambiare il segno alla parte immaginaria. $$z' = a-bi = = d ( \cos x - i \sin x ) e^{(-i)x} $$
Il coseno
$$ \cos x = \frac{e^{ix}+e^{-ix}}{2} $$
Dimostrazione. Ho il numero complesso z e il suo coniugato z' $$ z = \cos x + i \sin x = e^{ix} $$ $$z' = \cos x - i \sin x = e^{-ix} $$ Sommo membro a membro le due equazioni $$ ( \cos x + i \sin x ) + ( \cos x - i \sin x ) = e^{ix} + e^{-ix} $$ $$ \cos x + i \sin x + \cos x - i \sin x = e^{ix} + e^{-ix} $$ $$ 2 \cos x = e^{ix}+ e^{-ix} $$ Esplicito il coseno di x $$ \cos x = \frac{e^{ix}+ e^{-ix}}{2} $$ E ottengo la formula che volevo dimostrare.
Il seno
$$ \sin x = \frac{e^{ix}-e^{-ix}}{2i} $$
Dimostrazione. Ho il numero complesso z e il suo coniugato z' $$ z = \cos x + i \sin x = e^{ix} $$ $$z' = \cos x - i \sin x = e^{-ix} $$ Sottraggo membro a membro le due equazioni $$ ( \cos x + i \sin x ) - ( \cos x - i \sin x ) = e^{ix} - e^{-ix} $$ $$ \cos x + i \sin x - \cos x + i \sin x = e^{ix} - e^{-ix} $$ $$ 2 i \sin x = e^{ix} - e^{-ix} $$ Esplicito il seno di x $$ \sin x = \frac{e^{ix} - e^{-ix}}{2i} $$ E ottengo la formula che volevo dimostrare.
Note
Alcune note a margine sulle formule di Eulero
- Quando l'angolo è 180°, ovvero $ \alpha = \pi $ radianti, la formula di Eulero diventa $$ e^{\pi i} + 1 = 0 $$ che comprende tutti i cinque simboli più importanti della matematica ( 1, 0, $ e $, $ i $, $ \pi $ ).
Dimostrazione. Considero l'angolo $ \alpha = \pi $ nella formula di Eulero. $$ e^{i \pi} = \cos \pi + i \cdot \sin \pi $$ Il coseno di 180° è -1 mentre il seno di 180° è 0. $$ e^{i \pi} = -1 + i \cdot 0 $$ $$ e^{i \pi} = -1 $$ $$ e^{i \pi} + 1 = 0 $$
E così via.
