Numeri immaginari

Un numero immaginario è un numero complesso del tipo (0,b) con la parte reale nulla. $$(0,b)$$ oppure bi in forma algebrica. $$b \cdot i$$ dove i è l'unità immaginaria i=(0,1).

In pratica è una coppia di numeri reali in cui il primo elemento è sempre nullo.

Dal punto di vista geometrico l'insieme dei numeri immaginari corrisponde ai punti dell'asse delle ordinate (Im) del piano di Gauss.

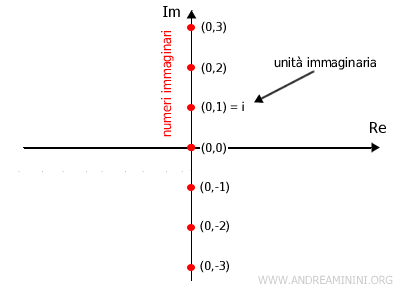
Un numero immaginario particolarmente importante è il numero (0,1) detto unità immaginaria.

L'unità immaginaria

L'unità immaginaria è il numero immaginario (0,1). Si indica con il simbolo i oppure j. $$i = (0,1)$$

Ecco l'unità immaginaria sul piano di Gauss.

Nota. In genere l'unità immaginaria è indicata con la lettera i nei testi matematici e con la lettera j nei testi di ingegneria. Il significato è sempre lo stesso $$i = j = (0,1)$$

L'unità immaginaria è importante perché il quadrato dell'unità immaginaria è -1

$$i^2 = (0,1)^2 = -1$$

Dimostrazione. Per dimostrare questo risultato calcolo il quadrato dell'unità immaginaria (0,1)² come prodotto del numero immaginario (0,1)*(0,1) per se stesso. $$(0,1)^2 = (0,1) \cdot (0,1)$$ Calcolo la moltiplicazione tra i due numeri complessi immaginari. $$(0,1)^2 = ( 0 \cdot 0-1 \cdot 1, 0 \cdot 1 + 1 \cdot 0)$$ $$(0,1)^2 = ( 0-1, 0 + 0)$$ $$(0,1)^2 = ( -1, 0)$$ Il risultato è il numero complesso reale meno uno. Pertanto, il quadrato dell'unità immaginaria i=(0,1) è i²=-1.

Questo è' particolarmente utile nel calcolo delle radici quadrate dei numeri reali negativi.

Esempio

La radice quadrata di -9 non può essere calcolata con i numeri reali

$$x = \sqrt{-9}$$

Posso però risolverla con i numeri complessi.

$$x = \sqrt{-1 \cdot 9}$$

Sapendo che il quadrato dell'unità immaginaria è meno uno i²=-1

$$x = \sqrt{i^2 \cdot 9}$$

$$x = i \cdot \sqrt{9}$$

Ora il radicando è un numero reale positivo, quindi posso calcolare la radice quadrata.

$$x = \pm i \cdot 3$$

Le soluzioni della radice quadrata di -9 sono i numeri complessi immaginari 0+3i e 0-3i ossia (0,3) e (0,-3).

$$x = \sqrt{-9} = \begin{cases} 0+3i \\ \\ 0 - 3i \end{cases}$$

Le due soluzioni sono due numeri complessi coniugati.

Le altre proprietà dell'unità immaginaria

In generale il prodotto tra l'unità immaginaria (0,1) e un numero complesso reale (a,0) è sempre un numero immaginario del tipo (0,a).

$$(a,0) \cdot (0,1) = (0,a)$$

Dimostrazione. Per dimostrare questa proprietà basta svolgere la moltiplicazione tra numeri complessi. $$(a,0) \cdot (0,1) = (a \cdot 0 - 0 \cdot 1, a \cdot 1 + 0 \cdot 0)$$ $$(a,0) \cdot (0,1) = (0 - 0, a + 0)$$ $$(a,0) \cdot (0,1) = (0, a)$$

Esempio

Moltiplico il numero complesso reale z1=(5,0) per l'unità immaginaria i=(0,1)

$$z_1 \cdot i = (5,0) \cdot (0,1)$$ $$z_1 \cdot i = (5 \cdot 0 - 0 \cdot 1, 5 \cdot 1 + 0 \cdot 0)$$ $$z_1 \cdot i = (0 - 0, 5 + 0)$$ $$z_1 \cdot i = (0, 5)$$

Il risultato finale è un numero immaginario.

Un esempio pratico

Considero due numeri immaginari

$$z_1 = (0,4)$$

$$z_2 = (0,3)$$

La somma dei due numeri immaginari è un altro numero immaginario.

$$z_1 + z_2 = (0,4) + (0,3) = (0+0,4+3) = (0,7)$$

Il prodotto tra i due numeri immaginari è un numero complesso reale

$$z_1 \cdot z_2 = (0,4) \cdot (0,3)$$

$$z_1 \cdot z_2 = (0 \cdot 0 - 4 \cdot 3,0 \cdot 3 + 4 \cdot 0)$$

$$z_1 \cdot z_2 = (0 - 12,0 + 0)$$

$$z_1 \cdot z_2 = (- 12, 0)$$

I numeri immaginari in forma algebrica

Un numero immaginario (0,b) posso scriverlo anche nella forma algebrica bi dove i è l'unità immaginaria i=(0,1) $$(0,b)=bi$$

Dimostrazione

Considero un numero immaginario qualsiasi (0,b)

$$z = (0,b)$$

Lo scrivo in forma algebrica

$$z = b \cdot i$$

Sapendo che l'unità immaginaria i=(0,1)

$$z = b \cdot i = b \cdot (0,1)$$

Calcolo la moltiplicazione e ottengo il numero immaginario nella forma (0,b)

$$z = b \cdot i = b \cdot (0,1) = (b \cdot 0 , b \cdot 1 )$$

Nota. In forma algebrica i numeri immaginari si calcolano come fossero monomi. Va però sottolineato che un numero immaginario non è un monomio perché l'unità immaginaria non è una variabile bensì una costante.

Le operazioni tra numeri immaginari

Per calcolare le operazioni matematiche tra numeri immaginari si seguono queste regole

• L'addizione tra numeri immaginari
  Dati due numeri immaginari z₁=(0,a) e z₂=(0,b) l'addizione si calcola sommando i coefficienti immaginari tra loro $$z_1 + z_2 = (0,a) + (0,b) = (0,a+b)$$ In forma algebrica $$z_1+z_2=a i + bi = (a+b)i$$
• La sottrazione tra numeri immaginari
  Dati due numeri immaginari z₁=(0,a) e z₂=(0,b) la differenza si calcola sottraendo il secondo coefficiente immaginario dal primo $$z_1 - z_2 = (0,a) - (0,b) = (0,a-b)$$ In forma algebrica $$z_1-z_2=a i - bi = (a-b)i$$
• La moltiplicazione tra numeri immaginari
  Il prodotto di due numeri immaginari z₁=(0,a) e z₂=(0,b) è un numero reale -ab $$z_1 \cdot z_2 = (0,a) \cdot (0,b) = -ab$$ In forma algebrica $$z_1 \cdot z_2 = ai \cdot bi = abi^2 =ab(-1) = -ab$$
• La divisione tra numeri immaginari
  La divisione di due numeri immaginari z₁=(0,a) e z₂=(0,b) è un numero reale. $$(0,a) : (0,b) = (a:b, 0)$$ in forma algebrica $$ai : bi = a:b$$
• La potenza dei numeri immaginari
  La potenza di un numero immaginario è uguale alla potenza del numero reale per la potenza dell'unità immaginaria. $$(ai)^n = a^n \cdot i^n$$ Dove la potenza dell'unità immaginaria si ripete con periodo quattro: i⁰=1, i¹=i, i²=-1, i³=-i, ...

Nota. L'addizione e la sottrazione sono due operazioni interne ai numeri immaginari perché il risultato è un altro numero immaginario. La moltiplicazione e la divisione, invece, non sono operazioni interne ai numeri immaginari perché il risultato è un numero reale, non è un numero immaginario.

Note a margine

Alcune note e osservazioni sui numeri immaginari.

• Lo zero è anche un numero immaginario
  Lo zero posso considerarlo come un numero immaginario, poiché posso pensarlo come il prodotto tra lo zero e l'unità immaginaria $$0 = 0 \cdot i$$
• I numeri immaginari non sono monomi
  Nelle operazioni matematiche, i numeri immaginari si comportano in modo simile ai monomi (ad esempio, $4i + 3i = 7i$), ma non lo sono, poiché l'unità immaginaria $i$ rappresenta un numero e non una variabile.

E così via.