La radice ennesima dell'unità
La radice n-esima dell'unità è un numero complesso z tale che la potenza ennesima di z è uguale a $$ z^n = 1 $$ Pertanto $$ \sqrt[n]{z^n} = \sqrt[n]{1} $$ $$ z = \sqrt[n]{1} $$
In forma trigonometrica le radici ennesime dell’unità sono:
$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \cdot \sin \frac{ 2k \pi }{n} $$
Mentre in forma esponenziale
$$ u_k = e^{\frac{2\pi i k}{n}}, \quad \text{con } k = 0, 1, 2, \ldots, n-1 $$
Dove k=0, 1, 2, ..., n-1
Spiegazione
Una radice \( n \)-esima dell’unità è un numero complesso \( u \) che soddisfa l’equazione: $$ u^n = 1 $$ dove \( n \) è un numero intero positivo.
In altre parole, una radice ennesima dell'unità è un numero complesso \( u \) che, elevato alla potenza \( n \), è uguale a \( 1 \).
$$ u^n =1 $$
In genere, una radice ennesima dell'unità si indica anche con \( \sqrt[n]{1} \) perché la radice ennesima di \( u^n=1 \) è la radice ennesima di 1.
$$ \sqrt[n]{u^n} = \sqrt[n]{1} $$
Quindi, posso scrivere anche
$$ u = \sqrt[n]{1} $$
Questo spiega perché il numero complesso $ u $ è una radice ennesima dell'unità.
Come trovare le radici dell’unità?
Le radici \( n \)-esime dell'unità $ u_k = \sqrt[n]{1} $ si calcolano utilizzando una delle seguenti formule:
- Forma trigonometrica $$ u_k = \cos \frac{2k \pi}{n} + i \sin \frac{2k \pi}{n}, \quad \text{con } k = 0, 1, 2, \ldots, n-1 $$
- Forma esponenziale $$ u_k = e^{\frac{2\pi i k}{n}}, \quad \text{con } k = 0, 1, 2, \ldots, n-1 $$
In entrambe le rappresentazioni \( k \) è l’indice che identifica ciascuna radice.
Il termine \( e^{\frac{2\pi i k}{n}} \) è la forma esponenziale corrispondente alla rappresentazione trigonometrica.
Nota. La forma esponenziale \( e^{\frac{2\pi i k}{n}} \) è molto utile, ma guai a calcolarla senza calcolatrice... dopo i primi \( \pi \) mi viene voglia di buttare tutto dalla finestra.
Le radici rappresentano i vertici di un poligono regolare inscritto nel cerchio unitario nel piano complesso.
In altre parole, queste radici non sono altro che i punti su un cerchio unitario, diviso in parti uguali.
Quante sono le radici dell'unità?
Le radici dell'unità sono infinite in teoria, poiché il cerchio unitario si ripete indefinitamente. Tuttavia, per un dato \( n \), esiste un numero finito di radici distinte.
In generale, si dimostra che le radici \( n \)-esime distinte dell’unità sono esattamente \( n \) e corrispondono ai valori \( k = 0, 1, \ldots, n-1 \).
$$ u_k = e^{\frac{2\pi i k}{n}}, \quad \text{con } k = 0, 1, 2, \ldots, n-1 $$
Quando ci sono più di due radici (n>2), sul piano complesso (piano di Gauss) le n radici distinte formano un poligono regolare di n lati inscritto in una circonferenza con centro nell'origine degli assi e raggio unitario (r=1), con uno dei vertici del poligono nel punto P(1;0).
Quindi, le radici ennesime mi permettono sia di dividere il cerchio in n parti uguali, sia di costruire un poligono regolare di n lati.
Per chiarire questo aspetto è meglio fare qualche esempio pratico.
Esempio: radici quadrate dell'unità (\( n = 2 \))
Per \( n = 2 \), cerco i numeri complessi \( u \) tali che:
$$ u^2 = 1 $$
Le radici sono due:
- \( u_0 = e^{\frac{2\pi i \cdot 0}{2}} = e^0 = 1 \)
- \( u_1 = e^{\frac{2\pi i \cdot 1}{2}} = e^{\pi i} = -1 \)
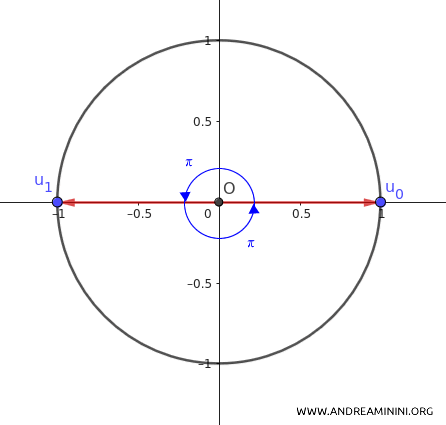
Questi due numeri complessi corrispondono ai punti opposti sul cerchio unitario nel piano complesso.
In questo caso il cerchio viene diviso a metà.
Nota. Lo stesso risultato può essere ottenuto usando la forma trigonometrica. Per \( n = 2 \), i numeri complessi \( u \) tali che \( u^2 = 1 \) si ottengono dalla formula:
$$ u_k = \cos \frac{2k\pi}{2} + i \sin \frac{2k\pi}{2}, \quad \text{con } k = 0, 1 $$
Calcolo ciascuna radice e le coordinate di ogni punto sul piano di Gauss:
- \( u_0 = \cos \frac{2 \cdot 0 \pi}{2} + i \sin \frac{2 \cdot 0 \pi}{2} = \cos 0 + i \sin 0 = 1 + i \cdot 0 \quad \Rightarrow \quad (1, 0) \)
- \( u_1 = \cos \frac{2 \cdot 1 \pi}{2} + i \sin \frac{2 \cdot 1 \pi}{2} = \cos \pi + i \sin \pi = -1 + i \cdot 0 \quad \Rightarrow \quad (-1, 0) \)
Questi due numeri complessi alle coordinate (1,0) e (-1,0) rappresentano i due estremi opposti del diametro del cerchio unitario, lungo l'asse reale del piano complesso.
Esempio: radici cubiche dell'unità (\( n = 3 \))
Per \( n = 3 \), cerco i numeri complessi \( u \) tali che :
$$ u^3 = 1 $$
Le radici sono tre:
- \( u_0 = e^{\frac{2\pi i \cdot 0}{3}} = e^0 = 1 \)
- \( u_1 = e^{\frac{2\pi i \cdot 1}{3}} = e^{\frac{2\pi i}{3}} \)
- \( u_2 = e^{\frac{2\pi i \cdot 2}{3}} = e^{\frac{4\pi i}{3}} \)
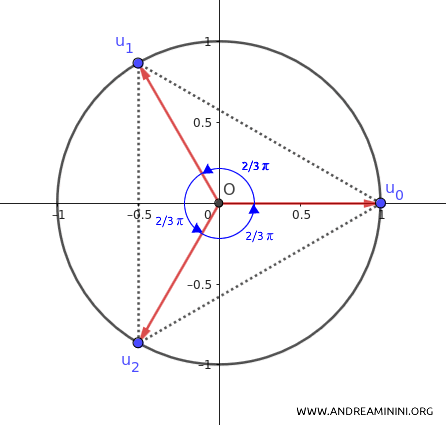
Questi tre numeri complessi dividono il cerchio unitario nel piano complesso in tre parti uguali e individuano i vertici di un triangolo equilatero inscritto nel cerchio.
Nota. Lo stesso risultato lo posso ottenere con i numeri complessi in forma trigonometrica.
Per \( n = 3 \) i numeri complessi \( u \) tali che $ u^3 = 1 $ li ottengo tramite la formula:
$$ u_k = \cos \frac{2k\pi}{3} + i \sin \frac{2k\pi}{3}, \quad \text{con } k = 0, 1, 2. $$
Calcolo ogni radice e ottengo:
- \( u_0 = \cos \frac{2 \cdot 0 \pi}{3} + i \sin \frac{2 \cdot 0 \pi}{3} = \cos 0 + i \sin 0 = 1 + i \cdot 0 \quad \Rightarrow \quad (1;0) \)
- \( u_1 = \cos \frac{2 \cdot 1 \pi}{3} + i \sin \frac{2 \cdot 1 \pi}{3} = \cos \frac{2\pi}{3} + i \sin \frac{2\pi}{3} = -\frac{1}{2} + i \frac{\sqrt{3}}{2} \quad \Rightarrow \quad \left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right) \)
- \( u_2 = \cos \frac{2 \cdot 2 \pi}{3} + i \sin \frac{2 \cdot 2 \pi}{3} = \cos \frac{4\pi}{3} + i \sin \frac{4\pi}{3} = -\frac{1}{2} - i \frac{\sqrt{3}}{2} \quad \Rightarrow \quad \left(-\frac{1}{2}, -\frac{\sqrt{3}}{2}\right) \)
Questi numeri complessi sono le coordinate dei vertici di un triangolo equilatero inscritto nel cerchio unitario nel piano complesso.
Ecco come puoi scrivere un esempio simile per \( n = 4 \), con parole diverse e lo stesso stile:
Esempio: radici quartiche dell'unità (\( n = 4 \))
Per \( n = 4 \), cerco i numeri complessi \( u \) tali che:
$$ u^4 = 1 $$
Le radici distinte sono quattro e possono essere espresse in forma esponenziale come segue:
$$ u_k = e^{\frac{2\pi i k}{4}}, \quad \text{con } k = 0, 1, 2, 3 $$
Calcolo ciascuna radice:
- \( u_0 = e^{\frac{2\pi i \cdot 0}{4}} = e^0 = 1 \)
- \( u_1 = e^{\frac{2\pi i \cdot 1}{4}} = e^{\frac{\pi i}{2}} = i \)
- \( u_2 = e^{\frac{2\pi i \cdot 2}{4}} = e^{\pi i} = -1 \)
- \( u_3 = e^{\frac{2\pi i \cdot 3}{4}} = e^{\frac{3\pi i}{2}} = -i \)
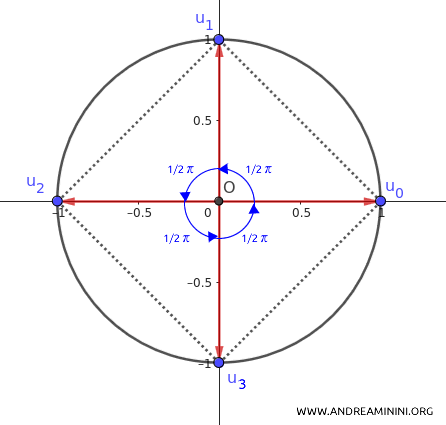
Questi numeri complessi rappresentano i vertici di un quadrato inscritto nel cerchio unitario nel piano complesso.
In questo caso, il cerchio viene diviso in 4 parti uguali.
In alternativa, possiamo esprimere le radici usando la forma trigonometrica:
$$ u_k = \cos \frac{2k\pi}{4} + i \sin \frac{2k\pi}{4}, \quad \text{con } k = 0, 1, 2, 3 $$
Calcolo ogni radice:
- \( u_0 = \cos \frac{2 \cdot 0 \pi}{4} + i \sin \frac{2 \cdot 0 \pi}{4} = \cos 0 + i \sin 0 = 1 + i \cdot 0 = (1, 0) \)
- \( u_1 = \cos \frac{2 \cdot 1 \pi}{4} + i \sin \frac{2 \cdot 1 \pi}{4} = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} = 0 + i \cdot 1 = (0, 1) \)
- \( u_2 = \cos \frac{2 \cdot 2 \pi}{4} + i \sin \frac{2 \cdot 2 \pi}{4} = \cos \pi + i \sin \pi = -1 + i \cdot 0 = (-1, 0) \)
- \( u_3 = \cos \frac{2 \cdot 3 \pi}{4} + i \sin \frac{2 \cdot 3 \pi}{4} = \cos \frac{3\pi}{2} + i \sin \frac{3\pi}{2} = 0 - i \cdot 1 = (0, -1) \)
Questi quattro numeri complessi corrispondono ai vertici di un quadrato inscritto nel cerchio unitario nel piano complesso.
Un esempio pratico
La radice quadrata dell'unità ha n=2 soluzioni
Per k=0 la prima soluzione è
$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \cdot \sin \frac{ 2k \pi }{n} $$
$$ \sqrt[2]{1} = \cos \frac{ 2 \cdot 0 \cdot \pi }{2} + i \cdot \sin \frac{ 2 \cdot 0 \cdot \pi }{2} $$
$$ \sqrt[2]{1} = \cos 0 + i \cdot \sin 0 $$
$$ \sqrt[2]{1} = 1 + i \cdot 0 $$
$$ \sqrt[2]{1} = 1 $$
Per k=1 la seconda soluzione è
$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \cdot \sin \frac{ 2k \pi }{n} $$
$$ \sqrt[2]{1} = \cos \frac{ 2 \cdot 1 \cdot \pi }{2} + i \cdot \sin \frac{ 2 \cdot 1 \cdot \pi }{2} $$
$$ \sqrt[2]{1} = \cos \frac{ 2\pi }{2} + i \cdot \sin \frac{ 2 \cdot \pi }{2} $$
$$ \sqrt[2]{1} = \cos \pi + i \cdot \sin \pi $$
$$ \sqrt[2]{1} = -1 + i \cdot 0 $$
$$ \sqrt[2]{1} = - 1 $$
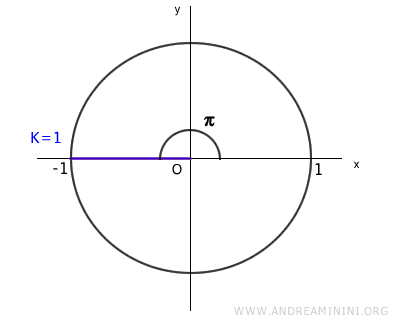
Nota. Per ogni valore k>1 le radici si ripetono ciclicamente alternandosi tra 1 e -1. Ad esempio, per k=2 la radice è 1. Per k=3 la radice è -1. E via dicendo. Per questa ragione nella radice quadrata dell'unità si considerano solo le prime due soluzioni distinte: 1 e -1. Più in generale, per una radice n-esima dell'unità si considerano le prime n soluzioni.
La dimostrazione
Parto dal presupposto che
$$ z^n = 1 $$
Riscrivo il numero complesso in forma trigonometrica
$$ [d \cdot ( \cos \alpha + i \sin \alpha) ]^n = 1 $$
Sapendo che 1 in forma triconometrica è cos(0)+i·sin(0)
$$ [d \cdot ( \cos \alpha + i \sin \alpha) ]^n = \cos 0 + i \cdot \sin 0 $$
Il modulo al secondo membro è uguale a 1
$$ [d \cdot ( \cos \alpha + i \sin \alpha) ]^n = 1 \cdot ( \cos 0 + i \cdot \sin 0 ) $$
Applico al primo membro la formula di De Moivre sulla potenza dei numeri complessi
$$ d^n \cdot ( \cos n\alpha + i \sin n\alpha) ) = 1 \cdot ( \cos 0 + i \cdot \sin 0 ) $$
L'uguaglianza è valida anche per i multipli di 2kπ
$$ d^n \cdot ( \cos n\alpha + i \sin n\alpha) ) = 1 \cdot [ \cos ( 0 + 2k \pi) + i \cdot \sin ( 0 + 2k \pi) ] $$
Per confronto tra i due membri deduco che
$$ \begin{cases} d^n = 1 \\ \\ n \alpha = 0 + 2k \pi \end{cases} $$
Pertanto l'angolo alfa è
$$ \begin{cases} d^n = 1 \\ \\ \alpha = \frac{ 2k \pi }{n} \end{cases} $$
Quindi, la radice n-esima dell'unità è
$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \cdot \sin \frac{ 2k \pi }{n} $$
per ogni k intero.
E così via.
