L'unità immaginaria dei numeri complessi

L'unità immaginaria è il numero complesso (0,1). Si indica con la lettera i $$ i = (0,1) $$ Il quadrato dell'unità immaginaria è il numero reale meno uno. $$ i^2 = -1 $$

L'unità immaginaria appartiene all'insieme dei numeri immaginari.

Si trova sul piano di Gauss alle coordinate (0,1)

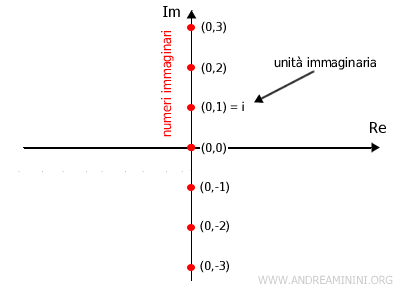
Nota. Nei libri di matematica l'unità immaginaria è indicata con la lettera minuscola i. Nei testi di ingegneria, invece, è spesso indicata con la lettera minuscola j. Il significato è comunque lo stesso $$ i = j = (0,1) $$

A cosa serve l'unità immaginaria?

L'unità immaginaria è molto utile perché il quadrato dell'unità immaginaria è -1

$$ i^2 = (0,1)^2 = -1 $$

Dimostrazione. Calcolo il quadrato dell'unità immaginaria (0,1)² come prodotto del numero immaginario (0,1)·(0,1) per se stesso. $$ (0,1)^2 = (0,1) \cdot (0,1) $$ Svolgo la moltiplicazione tra numeri complessi. $$ (0,1)^2 = ( 0 \cdot 0-1 \cdot 1, 0 \cdot 1 + 1 \cdot 0) $$ $$ (0,1)^2 = ( 0-1, 0 + 0) $$ $$ (0,1)^2 = ( -1, 0) $$ Il risultato finale è il numero complesso reale -1. Pertanto, il quadrato dell'unità immaginaria i=(0,1) è i²=-1.

Questa proprietà dell'unità immaginaria mi permette di calcolare la radice quadrata dei numeri negativi.

Un esempio pratico

La radice quadrata del numero reale negativo -16 non posso calcolarla con i numeri reali

$$ x = \sqrt{-16} $$

Tuttavia, posso risolverla usando i numeri complessi.

Riscrivo il radicando in questa forma equivalente.

$$ x = \sqrt{-1 \cdot 16} $$

Sapendo che il quadrato dell'unità immaginaria è meno uno i²=-1

Nel radicando sostituisco -1 con i²

$$ x = \sqrt{i^2 \cdot 16} $$

Il quadrato dell'unità immaginaria mi permette di far uscire l'unità immaginaria dalla radice quadrata.

$$ x = i \cdot \sqrt{16} $$

Adesso il radicando è un numero reale positivo (16).

Quindi posso risolvere la radice quadrata √16=4

$$ x = \pm 4 \cdot i $$

$$ x = 0 \pm 4 \cdot i $$

In questo modo ho trovato le soluzioni della radice quadrata di -16.

$$ x = \sqrt{-16} = \begin{cases} 0+4i \\ \\ 0 - 4i \end{cases} $$

Le soluzioni della radice quadrata del numero negativo -16 sono i numeri complessi coniugati 0+4i e 0-4i.

Le proprietà dell'unità immaginaria

L'unità immaginaria ha le seguenti proprietà

• Il quadrato dell'unità immaginaria è il numero reale -1 $$ i^2 = (0,1)^2 = -1 $$
• Il prodotto tra l'unità immaginaria (0,1) e un numero complesso reale (a,0) è sempre un numero immaginario del tipo (0,a). $$ (a,0) \cdot (0,1) = (0,a)$$

Dimostrazione. Per dimostrare questa proprietà basta svolgere la moltiplicazione tra numeri complessi. $$ (a,0) \cdot (0,1) = (a \cdot 0 - 0 \cdot 1, a \cdot 1 + 0 \cdot 0) $$ $$ (a,0) \cdot (0,1) = (0 - 0, a + 0) $$ $$ (a,0) \cdot (0,1) = (0, a) $$

Esempio

Moltiplico il numero complesso reale z=(7,0) per l'unità immaginaria i=(0,1)

$$ z \cdot i = (7,0) \cdot (0,1) $$ $$ z \cdot i = (7 \cdot 0 - 0 \cdot 1, 7 \cdot 1 + 0 \cdot 0) $$ $$ z \cdot i = (0 - 0, 7 + 0) $$ $$ z \cdot i = (0, 7) $$

Il risultato finale è un altro numero immaginario.

E così via.