Forma esponenziale dei numeri complessi
Un numero complesso è rappresentabile anche in forma esponenziale. $$ z = r \cdot (\cos α + i \cdot \sin α ) = r \cdot e^{i \cdot α} $$ Dove r è il modulo e l'argomento α ∈ (0,2π).
Dove e è il numero di Nepero ossia la base dei logaritmi naturali e=2.7182...
E' detta rappresentazione esponenziale.
Esempio. Un numero complesso z in forma trigonometrica con modulo unitario (r=1) e argomento a si scrive in forma esponenziale semplicemente eia. $$ z = (\cos \alpha + i \cdot \sin \alpha ) = e^{i \alpha} $$
Perché usare la forma esponenziale dei numeri complessi?
E' usata nelle scienze applicate per calcolare più facilmente alcune operazioni matematiche sui numeri complessi.
Ad esempio, se già conosco il modulo e la fase (argomento) posso trovare più rapidamente la radice n-esima o la potenza n-esima del numero complesso.
Nota. Il numero complesso coniugato (x-iy) del numero z=x+iy nella forma esponenziale è $$ r \cdot (\cos α - i \cdot \sin α ) = r \cdot e^{-i \cdot α} $$
La dimostrazione
Il numero complesso in forma esponenziale si ottiene tramite la formula di Eulero
$$ r ( \cos \alpha + i \cdot \sin \alpha) = r \cdot e^{i \cdot \alpha} $$
La formula di Eulero mi permette di convertire la forma trigonometrica del numero complesso nella forma esponenziale
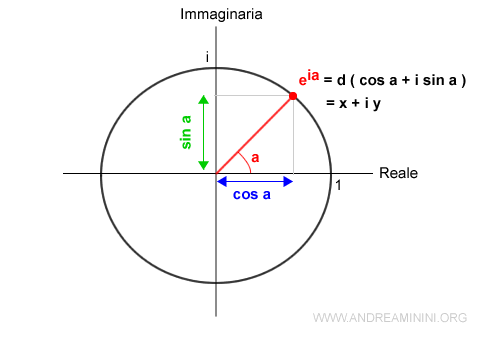
Scrivere z=a+bi, z=r(cos α + i sin α) oppure z=r·eiα indica lo stesso punto (x,y) sul piano complesso di Gauss.
Come passare dalla forma algebrica alla forma esponenziale
Se ho un numero complesso in forma algebrica z=a+bi
$$ z = a+ i \cdot i $$
Per convertire un numero complesso in forma algebrica z=a+bi in forma polare, devo prima trasformarlo in forma trigonometrica.
Una volta convertito in forma trigonometrica (polare) conosco già sia il modulo che l'argomento (fase). Quindi, riscriverlo in forma esponenziale non richiede calcoli.
Esempio
Considero il numero complesso
$$ z = 3+2i $$
Sul piano di Gauss si trova nel punto (3,2).
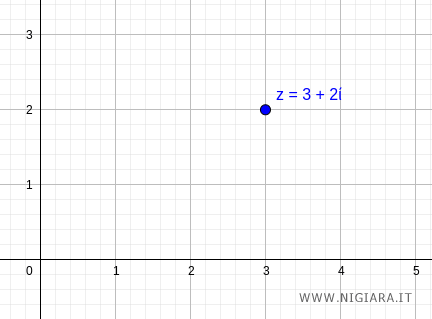
Lo converto in forma trigonometrica
Calcolo il modulo del numero complesso
$$ r = \sqrt{3^2+2^2} = \sqrt{9+4} =\sqrt{13} = 3.61 $$
Calcolo l'argomento del numero complesso
$$ \alpha = \arctan \frac{2}{3} = 33.69° $$
Quindi, il numero complesso in forma trigonometrica
$$ z = 3.61 \cdot ( \cos 33.69° + i \cdot \sin 33.69° ) $$
Sul piano di Gauss indica lo stesso punto (3,2) di prima ma questa volta usando le coordinate polari [ 3.61 , 33.69° ]
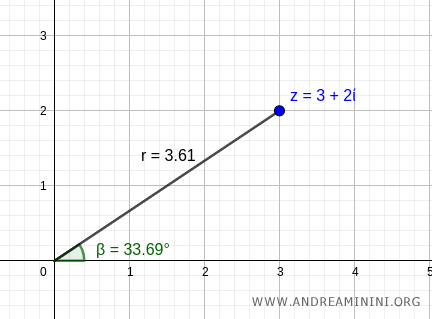
A questo punto riscrivo il numero complesso in forma esponenziale tramite la formula di Eulero
Non devo fare altri calcoli perché già conosco il modulo r=3.61 e l'argomento α=33.69°
$$ z = 3.61 \cdot e ^ {i \cdot 33.69° } $$
Le due forme indicano lo stesso numero complesso ossia lo stesso punto sul piano di Gauss.
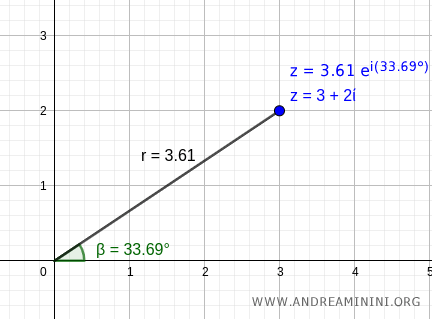
Nota. Allo stesso modo non richiede calcoli passare dalla forma esponenziale alla forma trigonometrica, essendo già noti sia il modulo che l'argomento
Come passare dalla forma esponenziale alla forma algebrica
Per trasformare un numero complesso in forma algebrica devo prima trasformarlo in forma trigonometrica.
Esempio
Ho un numero complesso in forma esponenziale
$$ z = 3 \cdot e^{i \frac{\pi}{6} } $$
Dove l'argomento (angolo) è π/6 e il modulo è 3.
Lo trasformo in forma trigonometrica.
$$ z = 3 \cdot ( \cos \frac{\pi}{6} + i \cdot \sin \frac{\pi}{6} ) $$
Per ottenere la forma algebrica/cartesiana calcolo i valori del seno e del coseno
$$ z = 3 \cdot ( \frac{\sqrt{3}}{2} + i \cdot \frac{1}{2} ) $$
$$ z = \frac{3 \sqrt{3}}{2} + i \cdot \frac{3}{2} $$
Il risultato è il numero complesso in forma algebrica.
Nota. La parte reale del numero complesso in forma algebrica misura le coordinate sull'asse delle ascisse. $$ x= \frac{3 \sqrt{3}}{2} $$ La parte immaginaria del numero complesso misura le coordinate sull'asse delle ordinate. $$ y= \frac{3}{2} $$
Le operazioni tra numeri complessi in forma esponenziale
Dati due numeri complessi in forma esponenziale
$$ z_1 = r_1 ( \cos \alpha + i \sin \alpha ) = r_1 \cdot e^{i \alpha} \\ z_2 = r_2 ( \cos \beta + i \sin \beta ) = r_2 \cdot e^{i \beta} $$
$$ z_1 \cdot z_2 = ( r_1 \cdot e^{i \alpha } ) \cdot ( r_2 \cdot e^{i \beta} ) = ( r_1 \cdot r_2 ) \cdot e^{i(\alpha+\beta)} $$
$$ \frac{z_1}{z_2} = \frac{r_1 \cdot e^{i \alpha }}{r_2 \cdot e^{i \beta}} = ( \frac{r_1}{r_2} ) \cdot e^{i(\alpha-\beta)} $$
$$ z_1^n = r_1^n \cdot e^{i \alpha \cdot n } $$
$$ \sqrt[n]{z_1} = r_1^{\frac{1}{n}} \cdot e^{i \cdot \frac{(\alpha+2πk)}{n} } $$
$$ \sqrt[n]{z_1^m} = r_1^{\frac{m}{n}} \cdot e^{i \cdot m \cdot \frac{(\alpha+2πk)}{n} } $$
Nota. Se conosco il modulo e la fase (argomento) del numero complesso posso calcolare più rapidamente tutte le operazioni matematiche rispetto alla forma trigonometrica o algebrica.
E così via.
