I paradossi nella logica
Cosa sono i paradossi
Un paradosso è un'affermazione o un ragionamento che contraddice l'intuizione comune ma che in realtà è corretta.
Si parla di paradosso anche per indicare una contraddizione logica (A e non A).
In questi casi si dovrebbe parlare più propriamente di antinomie.
Tuttavia, spesso nella letteratura logico-matematica le antinomie sono indicate come "paradossi". Ad esempio, il paradosso del mentitore è un antinomia.
La differenza tra paradossi e antinomie. A differenza dei paradossi le antinomie sono vere e proprie contraddizioni logiche. Spesso da una contraddizione può nascere da una contraddizione. Il concetto di paradosso è però più ampio. Può originare da aspetti ambigui di una teoria o di un ragionamento ed evidenziarne i limiti.
Un esempio pratico
Per spiegare i paradossi generati dalle contraddizioni logiche (antinomie) faccio un esempio pratico noto come il paradosso del mentitore.
La seguente proposizione è vera.

Tuttavia, se la proposizione "io sto mentendo" è vera (A=vera), allora anche l'affermazione "io sto mentendo" è falsa (A=falsa).
Quindi la proposizione "io sto mentendo" (A) implica la proposizione "io non sto mentendo" (¬A).
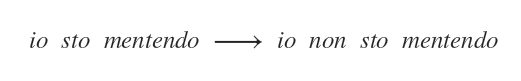
Le due proposizioni sono però l'una la negazione dell'altra.
Non possono verificarsi insieme.

Si tratta di una contraddizione perché la conclusione contraddice la sua stessa premessa.
$$ \begin{array}{cc|c} A & ¬A & A∧(¬A) \\ \hline F & V & F \\ V & F & F \end{array} $$
Ma se la premessa è falsa ...allora anche la conclusione non è vera. E così via in un loop che itera all'infinito.
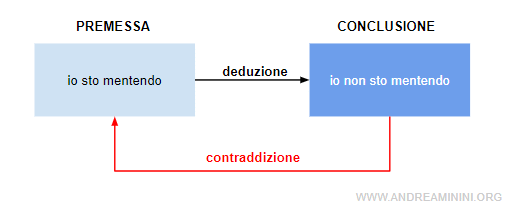
Questo è un esempio classico di paradosso (antinomia).
Nota. E' soltanto uno dei più semplici e conosciuti, ce ne sono molti altri ben più complessi. Nel calcolo logico-matematico le situazioni paradossali non sono rare.
E così via.
