L'implicazione materiale
L'implicazione materiale è una proposizione composta che mette in relazione una proposizione antecedente (A) con un'altra proposizione conseguente (B). Se la proposizione A è vera allora anche la proposizione B è vera. E' rappresentata con il simbolo di una freccia $$ A \rightarrow B $$ oppure $$ A \Rightarrow B $$
La precedente notazione si legge "A implica B", "da A segue B" oppure "se A allora B".
L'implicazione materiale è anche detta condizionale.
Questa è la tavola di verità dell'implicazione logica.
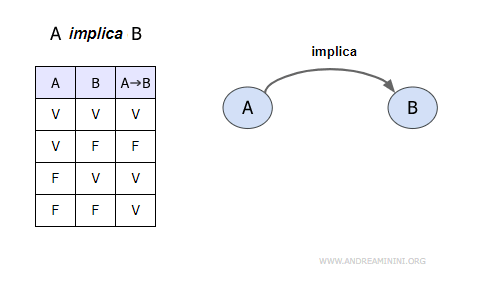
L'implicazione materiale A→B è equivalente all'enunciato ¬A ∨ B
$$ A→B \Longleftrightarrow ¬A ∨ B $$
E' un'equivalenza logica perché si ottengono gli stessi valori di verità con entrambi gli enunciati.
Nota. L'implicazione materiale è falsa (F) solo quando la proposizione antecedente (A) è vera e la proposizione seguente (B) è falsa. In tutti gli altri casi l'implicazione materiale A→B è vera (V). $$ \begin{array}{cr|c} A & B & A→B \\ \hline V & V & V \\ \color{red}V & \color{red}F & \color{red}F \\ F & V & V \\ F & F & V \end{array} $$ Pertanto, nell'implicazione materiale A è condizione sufficiente per B mentre B è condizione necessaria per A.
La differenza tra l'implicazione nella logica e nel linguaggio comune
La logica matematica indaga solo sulla correttezza formale delle proposizioni. Non indaga sul contenuto. Quindi, non occorre che le proposizioni siano vere o false, né che ci sia una relazione di causa effetto tra le proposizioni A e B.
C'è una differenza tra l'implicazione nella logica e nel linguaggio comune.
- Linguaggio comune. Nel linguaggio comune quando dico "se A allora B" lascio intendere una relazione di causa ed effetto tra la proposizione antecedente e conseguente.
Esempio. Se "piove" allora "prendo l'ombrello".
- Logica matematica. Nella logica matematica conta soltanto la correttezza formale del ragionamento. Non si indaga se le proposizioni sono vere o false, né se esiste una relazione di causa-effetto tra loro.
Esempio. Se "piove" allora "squilla il telefono".
Un esempio pratico
Considero due proposizioni A e B
$$ A = \text{8 è un numero pari} $$
$$ B = \text{8 è divisibile per due} $$
L'implicazione materiale A→B è vera (V) perché sia A che B sono vere.
$$ \begin{array}{cr|c} A & B & A→B \\ \hline \color{red}V & \color{red}V & \color{red}V \\ V & F & F \\ F & V & V \\ F & F & V \end{array} $$
Esempio 2
Considero due proposizioni A e B
$$ A = \text{8 è un numero pari} $$
$$ B = \text{8 è divisibile per tre} $$
L'implicazione materiale A→B è falsa (F) perché A è vera ma B è falsa.
$$ \begin{array}{cr|c} A & B & A→B \\ \hline V & V & V \\ \color{red}V & \color{red}F & \color{red}F \\ F & V & V \\ F & F & V \end{array} $$
Nota. Se A è vera e B è falsa, l'implicazione A→B è falsa perché viene contraddetta/smentita dai fatti.
Esempio 3
Considero due proposizioni A e B
$$ A = \text{8 è un numero dispari} $$
$$ B = \text{8 è divisibile per due} $$
L'implicazione materiale A→B è vera (V) perché A è falsa. Il valore di verità di B è ininfluente. In questo caso B è vera.
$$ \begin{array}{cr|c} A & B & A→B \\ \hline V & V & V \\ V & F & F \\ \color{red}F & \color{red}V & \color{red}V \\ F & F & V \end{array} $$
Nota. Se A è falsa e B è vera o falsa, resta comunque valida l'implicazione A→B. Il fatto che A sia falsa non mi permette di affermare nulla sull'implicazione A→B. Viceversa, se A è vera e B è falsa, l'implicazione A→B è falsa perché non è confermata dai fatti. I fatti dimostrano il contrario.
Esempio 4
Considero due proposizioni A e B
$$ A = \text{8 è un numero dispari} $$
$$ B = \text{8 è divisibile per tre} $$
L'implicazione materiale A→B è vera (V) perché A è falsa. Il valore di verità di B è ininfluente. In questo caso B è falsa.
$$ \begin{array}{cr|c} A & B & A→B \\ \hline V & V & V \\ V & F & F \\ F & V & V \\ \color{red}F & \color{red}F & \color{red}V \end{array} $$
Nota. Vale lo stesso discorso già fatto per l'esempio 3. Se A è falsa, il valore di verità di B può essere vero o falso. In questo caso l'implicazione A→B non viene smentita, né confermata dai fatti. Pertanto, l'implicazione A→B resta vera.
L'implicazione stretta o formale
La logica greca distingue tra due tipi di implicazioni
- Implicazione materiale (o filoniana)
Nella logica greca l'implicazione materiale è anche detta implicazione filoniana da Filone di Megara. $$ \begin{array}{cr|c} A & B & A→B \\ \hline V & V & V \\ \color{red}V & \color{red}F & \color{red}F \\ F & V & V \\ F & F & V \end{array} $$ E' detta filoniana per distinguerla dall'implicazione stretta o formale. - Implicazione stretta o formale
Nell'implicazione stretta è impossibile che A sia vera e B falsa. Se A è vera, allora necessariamente B è vera. E' impossibile il contrario. $$ A \Rightarrow B $$ L'implicazione stretta è usata per affermare una verità logica.
La differenza tra implicazione e deduzione
L'implicazione e la deduzione sono concetti diversi anche se spesso confusi tra loro perché hanno un simbolo simile (una freccia).
- L'implicazione (A→B)
L'implicazione (A→B) è un connettivo logico. Se A è vera anche B è vera. Essendo un connettivo logico non devo provare che la proposizione A sia effettivamente vera. Inoltre, nella tavola di verità è ammesso anche il caso contrario (A falsa) $$ \begin{array}{cr|c} A & B & A→B \\ \hline V & V & V \\ V & F & F \\ F & V & V \\ F & F & V \end{array} $$ - La deduzione (A⇒B)
La deduzione (A⇒B) non è un connettivo logico ma una forma di ragionamento detta anche modus ponens. Se A è vera anche B è vera. Rispetto all'implicazione ci sono due importanti differenze- Essendo un ragionamento, nella deduzione devo dimostrare che le premesse siano effettivamente vere per confermare la conclusione (B), perché partendo da premesse false potrei giungere a una conclusione formalmente corretta ma falsa.
- Nella deduzione non è considerato il caso contrario. Se la proposizione A è falsa, non posso affermare nulla su B che può essere sia vera che falsa. Pertanto, la deduzione e l'implicazione hanno tavole di verità diverse

Nota. Nella deduzione non sono ammesse le forme di ragionamento del tipo $$ (A \rightarrow B ) ∧ B \Rightarrow A $$ $$ ( A \rightarrow B ) ∧ ¬A \Rightarrow ¬B $$
E così via.
