Le proposizioni logiche

Una proposizione logica è un enunciato che può essere vera o falsa.

Un enunciato è una proposizione composta da parole o da simboli che ha un significato (es. "tutti gli uomini sono mortali", "a+a=2a").

Sono proposizioni solo le affermazioni oggettive. Non importa che siano vere o false.

Quest'ultima informazione (vero o falso) è detta valore di verità della proposizione.

Nota. Non sono proposizioni logiche le affermazioni soggettive (es. "è bello") perché valgono solo per la persona che le esprime ma non per tutti. Non sono proposizioni logiche anche le affermazioni prive di significato, le domande, i comandi, le previsioni sul futuro, ecc.

Una proposizione non può essere contemporaneamente vera e falsa. Se è vera non è falsa, e viceversa.

Un esempio pratico

Un esempio di proposizione logica è la seguente:

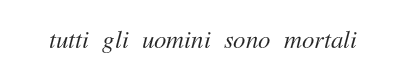
Se considero gli uomini con il simbolo A e i mortali con il simbolo B, posso riscrivere la proposizione anche in una forma matematica (A=B).

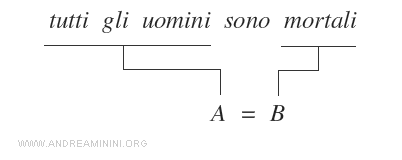
Le lettere A e B sono dette variabili logiche. Mi permettono di scrivere la proposizione in modo più compatto.

Il valore di verità di questa proposizione è vero.

Nota. Non è importante che abbia un valore di verità vero. Potrebbe anche essere falso. Quello che conta nel ragionamento logico è associare alla proposizione un valore di verità di partenza ( vero o falso ).

I valori di verità

Alle proposizioni logiche può essere associato un valore di verità.

Quali sono i valori di verità?

Nella logica classica esistono solo due valori di verità;

• Vero
  La proposizione logica è vera.
• Falso
  La proposizione logica è falsa

Spesso i valori di verità sono scritti in inglese True (vero) e False (falso).

A volte sono anche indicati brevemente con le lettere V (vero) e F (falso) oppure con l'abbreviazione inglese T (true) o F (false).

Essendo solo due, è anche possibile indicare i valori di verità con i numeri 1 (vero) e 0 (falso) della logica binaria.

Ecco le varie rappresentazioni dei valori di verità.

VERO	TRUE	V	T	1
FALSO	FALSE	F	F	0

Il significato è sempre lo stesso.

La differenza tra la logica classica e le altre logiche. In questi appunti mi limito a parlare della logica classica dove esistono due soli valori di verità (vero o falso). Tuttavia, credo sia utile accennare che non esiste solo la logica classica nel ragionamento logico. Esistono anche altre logiche (logiche non classiche) in cui i valori di verità sono più di due. Ad esempio, la logica fuzzy ne ammette molti di più, perché include l'incertezza nel ragionamento logico. Viceversa, la logica classica si basa esclusivamente sulla certezza.

Le proposizioni semplici e composte

Esistono due tipi di proposizioni

• Le proposizioni semplici
  Le proposizioni semplici sono composte da un solo predicato (forma verbale) ossia da una frase di senso compiuto formata da un soggetto e un predicato. Non possono essere spezzate in proposizioni più semplici tramite i connettivi logici. Sono anche dette proposizioni elementari, primitive o atomiche.

  Esempio. La frase "prendo l'ombrello" è una proposizione semplice. C'è un soggetto e un predicato.

• Le proposizioni composte
  Le proposizioni logiche sono due o più proposizioni legate tra loro da connettivi logici (and, or, not, se e solo se, se ... allora, ecc.). Il significato di una proposizione composta è diverso rispetto a quello delle singole proposizioni che la compongono. Se una proposizione è composta da più di due proposizioni, le regole di precedenza posso definirle tramite l'utilizzo delle parentesi come in algebra. Le espressioni composte sono anche dette proposizioni molecolari o espressioni logiche.
  

  Esempio. La frase "se piove prendo l'ombrello" è una proposizione composta da due proposizioni logiche semplici. La prima proposizione semplice "piove?" e la seconda proposizione semplice "prendo l'ombrello". Si tratta di una forma "se ... allora". Se la prima proposizione è vera, allora è vera anche la seconda. Nel caso delle proposizioni composte è molto utile rappresentare i valori di verità tramite una tavola di verità.

Le deduzioni logiche

Più preposizioni possono essere legate tra loro tramite in discorso con il metodo deduttivo.

In una deduzione c'è sempre una premessa e una conclusione.

Il compito della logica matematica è stabilire se a partire da una premessa, si può dedurre una conclusione.

Nota. Non è compito della logica matematica stabilire se le premesse e le conclusioni siano vere o false. Ciò che conta è la correttezza del calcolo logico (andreaminini.org). E' un aspetto della logica matematica che vale la pena sottolineare perché spesso viene fraintesa.

Il percorso non è però privo di ostacoli.

In alcuni casi ci si può imbattere nelle contraddizioni che danno vita a veri e propri paradossi.

E così via.