La negazione logica
La negazione è un connettivo logico che nega il valore di verità (vero o falso) di una proposizione semplice o composta (A). Si indica con i simboli ¬ o ~ prima della variabile logica oppure con un trattino sopra la variabile logica $$ ¬A \ \ , \ \ \text{~}A \ \ , \ \ \bar{A} $$ In tutti i casi si legge "non A".
Ecco la tavola di verità della negazione
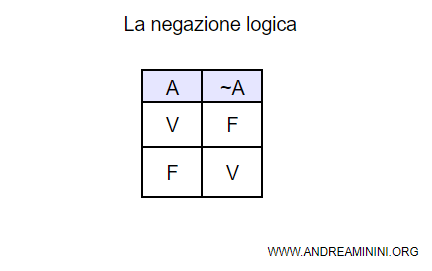
Se la proposizione A è vera, la negazione della proposizione ¬A è falsa.
$$ ¬( \text{vero}) = \text{falso} $$
Se la proposizione A è falsa, la negazione della proposizione ¬A è vera.
$$ ¬( \text{falso}) = \text{vero} $$
Nota. In pratica la negazione logica mi permette di ottenere il valore di verità opposto di una proposizione logica. La logica classica ha solo due valori di verità: vero e falso. Pertanto, l'opposto di vero è falso e viceversa.
A parità di condizioni, la negazione ha la precedenza su tutti gli altri connettivi logici ossia deve essere svolta prima degli altri.
Un esempio pratico
Considero la proposizione logica è "vado a casa"
$$ P = \text{vado a casa} $$
La negazione della proposizione è "non vado a casa"
$$ ¬P = \text{non vado a casa} $$
In questo modo ho ottenuto il significato opposto della proposizione iniziale.
Esempio 2
Considero la proposizione logica Q = "non vado a casa"
$$ Q = \text{non vado a casa} $$
La negazione della proposizione Q è "vado a casa"
$$ ¬Q = \text{vado a casa} $$
Anche in questo caso ottengo una proposizione con il significato opposto rispetto a quella iniziale.
La doppia negazione
La doppia negazione di una proposizione non cambia il valore di verità della proposizione.
$$ \begin{array}{c|r|c} P & ¬P & ¬¬P \\ \hline V & F & V \\ F & V & F \end{array} $$
Esempio. Se la proposizione Q è $$ Q=\text{non vado a casa} $$ la negazione logica della proposizione ¬Q è $$ ¬Q = \text{vado a casa} $$ Spiegazione. Considero due proposizioni. $$ P=\text{vado a casa} $$ $$ Q=\text{non vado a casa} $$ Posso riscrivere "non" come ¬. $$ Q = ¬ ( \text{vado a casa} ) $$ Pertanto, è equivalente scrivere Q come la negazione di P $$ Q = ¬P $$ Ora nego entrambi i membri dell'equazione. La proposizione Q equivale alla doppia negazione di P. $$ ¬Q = ¬(¬P) $$ Sapendo che la negazione di Q è P ossia ¬Q=P $$ P = ¬(¬P) $$ allora la doppia negazione di P si annulla. In conclusione ¬(¬P) = "vado a casa"
In generale, se la negazione è ripetuta un numero pari di volte, il risultato è uguale alla proposizione di origine.
$$ ¬( ¬( \text{vero}) ) = ¬( \text{falso} ) = \text{vero} $$
Viceversa, se la negazione è ripetuta un numero dispari di volte, il risultato è la negazione della proposizione iniziale.
$$ ¬( ¬( ¬( \text{vero}) ) ) = ¬( ¬( \text{falso} ) ) = ¬( \text{vero} ) = \text{falso} $$
E così via.
