Teorema dei piani paralleli intersecati da un terzo piano

Quando un piano $ \pi $ interseca due piani paralleli $ \pi_1 $ e $ \pi_2 $, le intersezioni sono due rette parallele $ r_1 $ e $ r_2 $.

Questo si verifica perché, essendo $ \pi_1 $ e $ \pi_2 $ equidistanti e paralleli, il piano $ \pi $ li interseca formando due rette $ r_1 $ e $ r_2 $.

Poiché $ \pi $ mantiene lo stesso angolo di intersezione con entrambi i piani, le rette $ r_1 $ e $ r_2 $ risultano parallele.

Dimostrazione

Considero due piani paralleli $ \pi_1 $ e $ \pi_2 $.

Per definizione, la distanza tra $ \pi_1 $ e $ \pi_2 $ è costante, e i loro vettori normali sono proporzionali.

Un terzo piano $ \pi $ interseca $ \pi_1 $ nella retta $ r_1 $ e $ \pi_2 $ nella retta $ r_2 $.

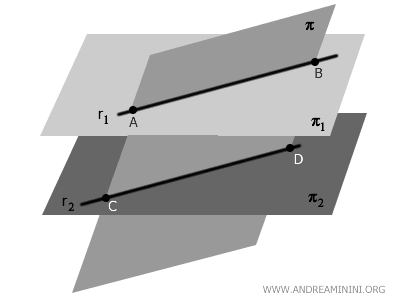
dimostrazione

Poiché $ \pi_1 \parallel \pi_2 $, il piano $ \pi $ li taglia mantenendo lo stesso angolo con entrambi.

Le rette $ r_1 $ e $ r_2 $ appartengono a $ \pi $, quindi giacciono sullo stesso piano.

Considero due punti $ A, B \in r_1 $ e i loro corrispondenti punti proiettati $ A', B' \in r_2 $.

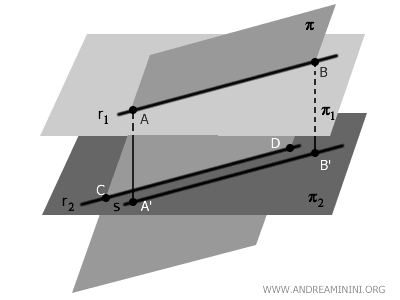
esempio

I segmenti perpendicolari $ AA' $ e $ BB' $ rappresentano la distanza costante tra $ \pi_1 $ e $ \pi_2 $, quindi sono tra loro paralleli e congruenti.

$$ AA' \parallel BB', \quad AA' \cong BB' $$

La geometria del piano $ \pi $ garantisce che $ r_1 $ e $ r_2 $ mantengano lo stesso orientamento. Per definizione, quindi, $ r_1 \parallel r_2 $.

In conclusione, le rette $ r_1 $ e $ r_2 $ sono parallele perché giacciono sullo stesso piano $ \pi $, mantengono lo stesso orientamento e rispettano la costanza della distanza tra $ \pi_1 $ e $ \pi_2 $.

E così via.