Equazioni delle superfici nello spazio

Nella geometria analitica dello spazio, una superficie è il luogo geometrico dei punti le cui coordinate cartesiane $x, y, z$ soddisfano un’equazione del tipo: $$ F(x, y, z) = 0 $$ Questa relazione stabilisce quali punti appartengono alla superficie.

L’equazione $F(x, y, z) = 0$ permette di verificare se un punto appartiene alla superficie, sostituendo $x, y, z$ e verificando se l’uguaglianza è soddisfatta e determinare la loro forma geometrica.

L’equazione può essere di forma molto semplice o molto complessa, a seconda della natura della superficie. 

Grazie all'equazione $F(x, y, z) = 0$ è possibile classificare le superfici (piani, quadriche, ecc.).

Superfici algebriche

Se la funzione $F(x, y, z)$ è un polinomio, la superficie si chiama superficie algebrica.

Si dice di ordine n (o grado n) se il polinomio è di grado $n$.

Le superfici di primo ordine sono i piani, descritti da equazioni lineari:

$$ ax + by + cz + d = 0 $$

Dove $a, b, c, d$ sono costanti.

Ad esempio, questa equazione definisce un piano: $$ 2x - 3y + z + 5 = 0 $$ Ecco come appare il piano nello spazio.

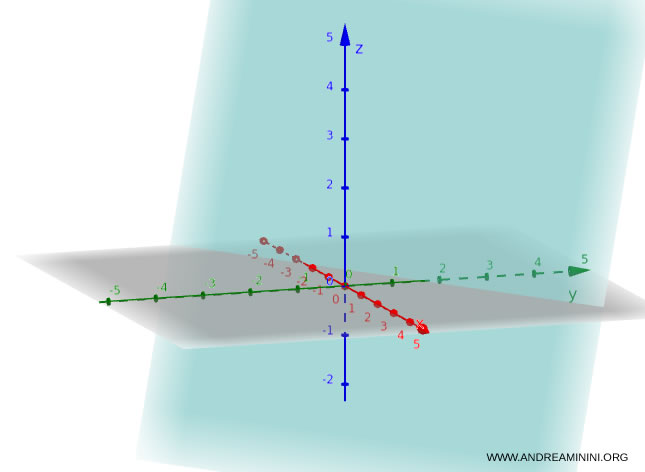
Per verificare se un punto appartiene al piano basta sostituire le sue coordinate nell'equazione e verificare se è soddisfatta. Ad esempio, il punto $(1, -1, 0)$ appartiene al piano? Verifico:$$2 \cdot 1 - 3 \cdot (-1) + 0 + 5 = 2 + 3 + 5 = 10 \neq 0$$ L'equazione non è soddisfatta, quindi il punto non appartiene al piano.

Le superfici di secondo ordine sono le quadriche, descritte da equazioni quadratiche.

Le superfici quadratiche

Le quadriche sono superfici definite da un’equazione polinomiale di secondo grado, di forma generale:

$$ ax^2 + by^2 + cz^2 + dxy + exz + fyz + gx + hy + iz + l = 0 $$

A seconda dei coefficienti, questa equazione descrive superfici molto diverse tra loro, come:

• ellissoidi
• iperboloidi
• paraboloidi
• coni
• cilindri

Ellissoide

L’ellissoide è la superficie che generalizza la sfera, ottenuta scalando i raggi lungo i tre assi cartesiani. La sua equazione è:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$

Se $a = b = c$, si tratta di una sfera.

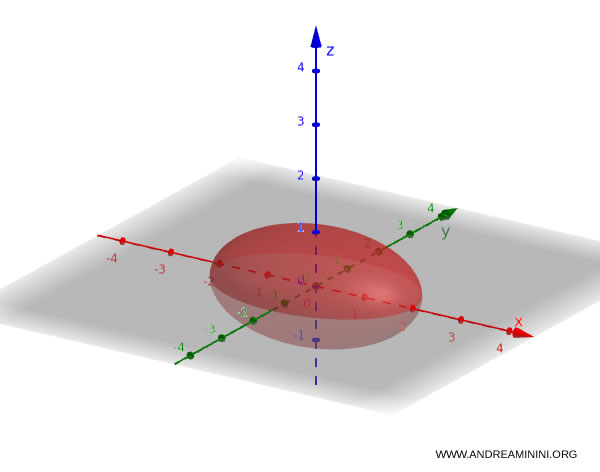
Ad esempio, considero l'equazione

$$ \frac{x^2}{9} + \frac{y^2}{4} + \frac{z^2}{1} = 1 $$

Questo è un ellissoide con semiassi $a = 3$, $b = 2$, $c = 1$.

Iperboloide

L’iperboloide è una superficie quadriche che può essere a una falda (a una sola parte), oppure a due falde (due parti separate).

L'equazione di un iperboloide a una falda è:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1 $$

L'equazione di un iperboloide a due falde è:

$$ - \frac{x^2}{a^2} - \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$

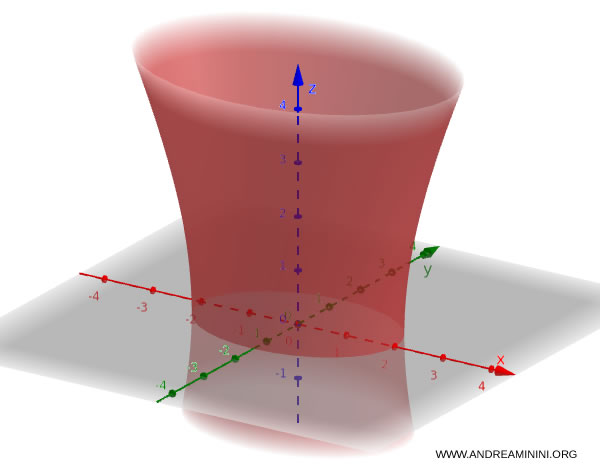
Ecco un esempio pratico di iperboloide a una falda $$ \frac{x^2}{4} + \frac{y^2}{9} - \frac{z^2}{16} = 1 $$ Descrive una superficie con un “collo” che si stringe al centro e si allarga verso l’alto e il basso.

Paraboloide

I paraboloidi sono superfici a forma “di parabola ruotata” e si dividono in paraboloidi ellittici o iperbolici.

L'equazione di un paraboloide ellittico è la seguente:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 2z $$

L'equazione di un paraboloide iperbolico è:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 2z $$

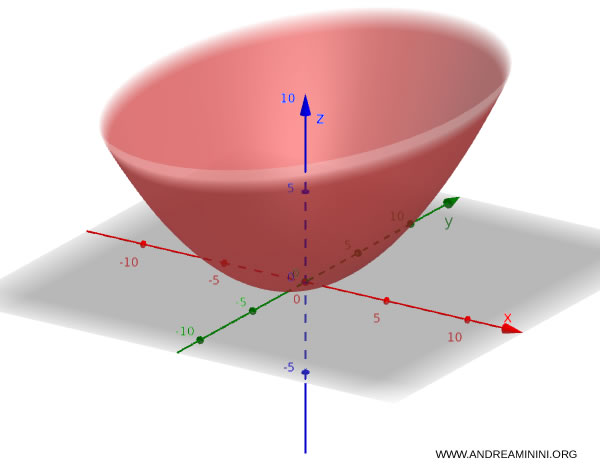
Ad esempio, questa equazione definisce un paraboloide ellittico $$ \frac{x^2}{4} + \frac{y^2}{9} = 2z $$

Cono

Il cono ha un vertice nell’origine e si estende in entrambe le direzioni. La sua equazione tipica è:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 0 $$

Ad esempio, questa equazione definisce un cono $$ \frac{x^2}{4} + \frac{y^2}{9} - \frac{z^2}{16} = 0 $$

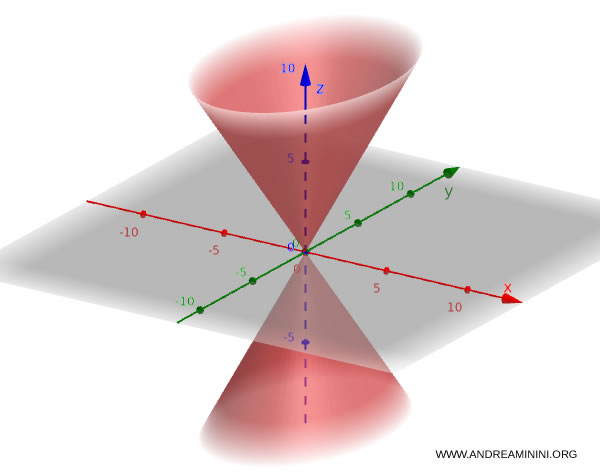
Cilindro

Una superficie cilindrica è costituita da rette (dette generatrici) traslate parallelamente a un asse.

Se l’equazione della superficie coinvolge solo due variabili (es. $x^2 - y - 1 = 0$), le soluzioni formano una curva nel piano corrispondente (es. Oxy) chiamata direttrice.

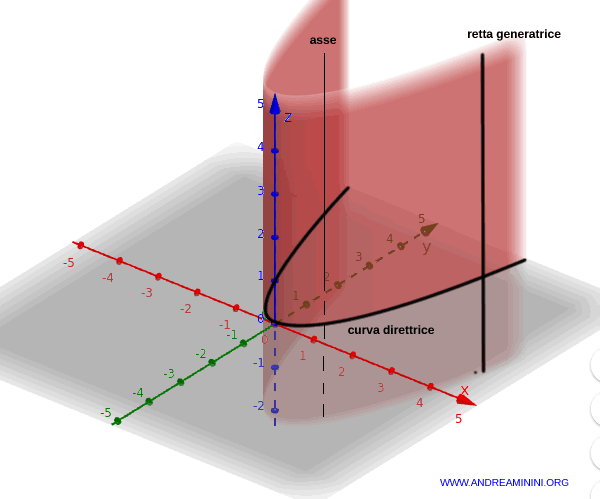
Traslando questa curva lungo l’asse libero (es. l’asse z), si genera tutta la superficie cilindrica.

La natura della direttrice definisce il tipo di cilindro:

• se è una parabola, il cilindro è parabolico
• se è un'ellisse il cilindro è ellittico
• se è una circonferenza il cilindro è circolare
• se è una iperbole il cilindro è iperbolico

L'equazione di una superficie cilindrica circolare è del tipo:

$$ x^2 + y^2 + a x + b y + c = 0 $$

Dove il termine in $z$ non compare, perché la superficie si estende all’infinito lungo $z$.

Questa equazione descrive una superficie cilindrica circolare purché i coefficienti soddisfano la seguente condizione:

$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$

In altre parole, solo se la curva direttrice sul piano xy rappresenta effettivamente una circonferenza.

Lo stesso discorso vale per gli alti piani xz e yz quando l'equazione contiene rispettivamente le variabili x e z oppure y e z.

Esempio. Ecco un esempio pratico di cilindro circolare nello spazio $$  \frac{x^2}{4} + \frac{y^2}{4} = 1 $$ Questa equazione descrive una superficie cilindrica circolare.

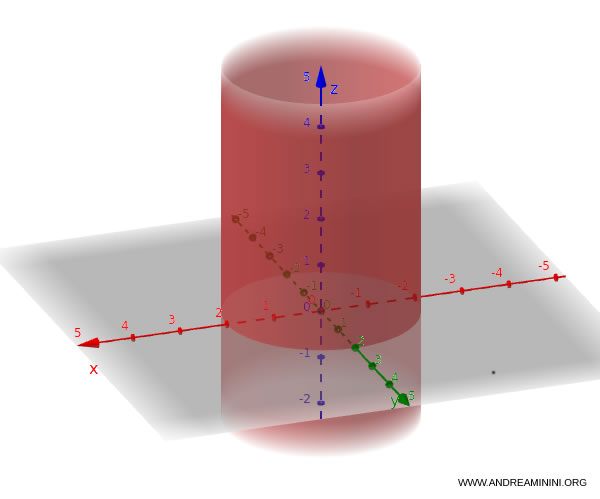
L'equazione di un cilindro ellittico è la seguente:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Quando i coefficienti $ a = b $  sono uguali, il cilindro ha la sezione circolare.

Esempio. Ecco un esempio pratico di cilindro nello spazio $$  \frac{x^2}{4} + \frac{y^2}{9} = 1 $$ Questa equazione rappresenta un cilindro con sezione ellittica.

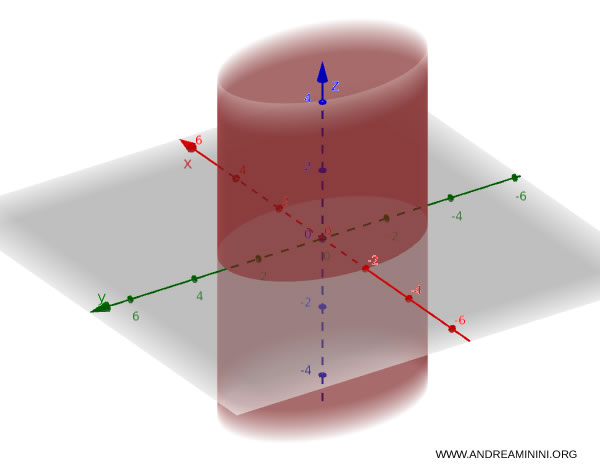
L'equazione di un cilindro iperbolico è:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Questa equazione vale per ogni valore di $z$ e rappresenta una superficie cilindrica iperbolica con asse parallelo all’asse $z$.

Esempio. Ecco un esempio di cilindro iperbolico. $$ \frac{x^2}{2} - \frac{y^2}{4} = 3 $$ In questo caso la direttrice è una iperbole sul piano xy mentre le rette generatrici sono parallele all'asse y.

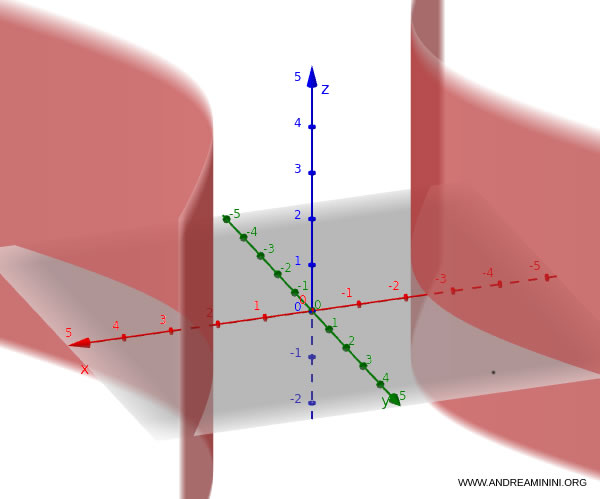
L'equazione di un cilindro parabolico è

$$y = k x^2 $$

Se questa relazione vale per ogni valore di $z$, allora rappresenta una superficie cilindrica parabolica con asse parallelo all’asse $z$.

Esempio. Considero la direttrice: $$ y = x^2.$$ La superficie cilindrica parabolica corrispondente è $ y = x^2, \quad z \in  \mathbb{R} $

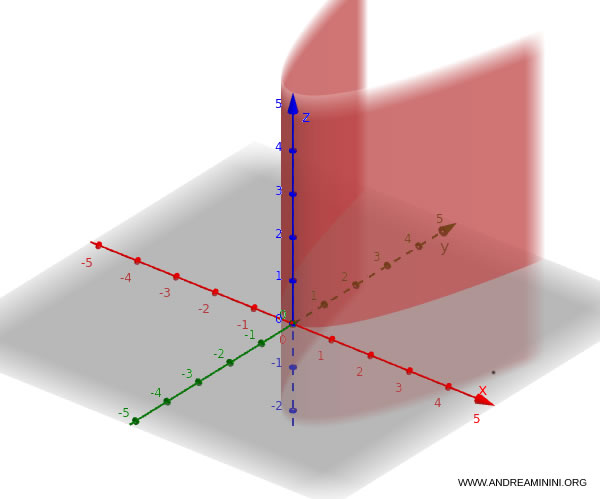
Spesso la si scrive in forma implicita: $$ y - x^2 = 0 $$ oppure $$ x - y^2 = 0 $$ Se l’equazione fosse in $x$ e $z$ l'equazione diventa: $$z = x^2$$ e si ottiene un cilindro parabolico con asse parallelo a $ y $.

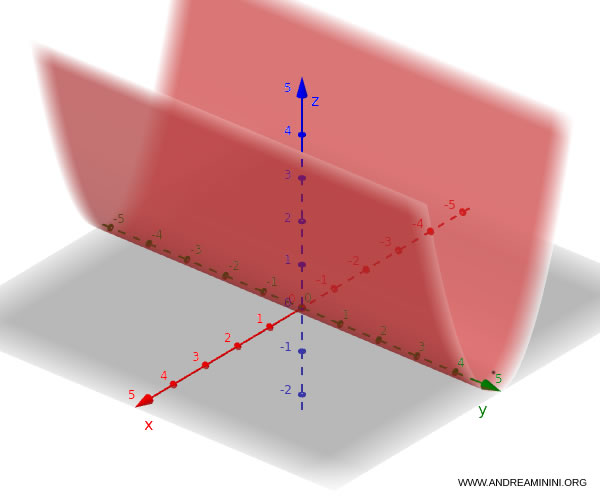
Se fosse in $y$ e $z$: $$z  = y^2$$ In questo caso si ottiene un cilindro parabolico con asse parallelo a $x$.

Questi esempi mostrano come le diverse quadriche siano tutte riconducibili a equazioni di secondo grado e ognuna ha una forma geometrica caratteristica.

Le sezioni delle superfici

Per studiare le curve ottenute con l'intersezione con i piano posso imporre dei vincoli fissando $z$ o $y$.

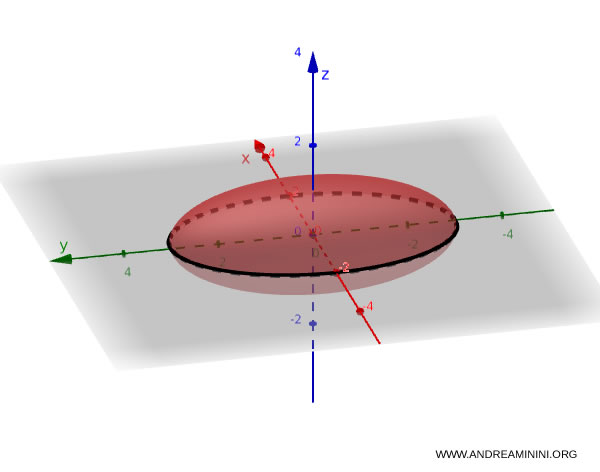
Ad esempio, considero l'ellissoide

$$ \frac{x^2}{9} + \frac{y^2}{4} + \frac{z^2}{1} = 1 $$

Fisso $z = 0$:

$$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$

Il risultato è una ellisse nel piano $xy$ ossia una sezione dell'ellissoide

Curva come intersezione di due superfici

Una curva può essere ottenuta come intersezione di due superfici nello spazio. $$ \begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases} $$

In altre parole, il luogo dei punti le cui coordinate $(x, y, z)$ soddisfano entrambe le equazioni è, in generale, una curva nello spazio.

La rappresentazione analitica di quella curva è proprio il sistema:

$$
\begin{cases}
F(x, y, z) = 0 \\
G(x, y, z) = 0
\end{cases}
$$

Questa è detta rappresentazione implicita della curva, perché non esprime $x, y, z$ in funzione di un parametro.

Esempio

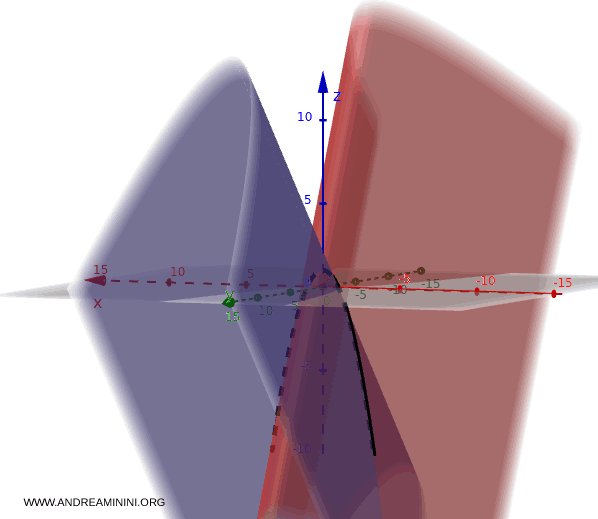
Considero un sistema composto da due superfici:

$$
\begin{cases}
x^{2} - y + z - 1 = 0 \\
x^{2} + 2y + z - 1 = 0
\end{cases}
$$

L’intersezione è la curva formata dai punti che risolvono entrambe le equazioni.

Spesso conviene parametrizzare la curva per lavorare meglio.

Ad esempio, parametrizzo la variabile $ t $.

$$ x = t $$

Poi eguaglio le equazioni delle superfici per trovare $ y $

$$ x^{2} - y + z - 1 = x^{2} + 2y + z - 1 $$

$$ x^{2} - y + z - 1 - (x^{2} + 2y + z - 1) = 0 $$

$$ x^{2} - y + z - 1 - x^{2} - 2y - z + 1 = 0 $$

$$ -3y = 0 $$

$$ y = 0 $$

Infine, sostituisco $ x=t $ e $ y = 0 $ in una equazione per trovare $ z $

$$ x^{2} + 2y + z - 1 = 0 $$

$$ t^2 + 2 \cdot 0 + z - 1 = 0 $$

$$ z = 1 - t^2 $$

Quindi la curva di intersezione ha le seguenti equazioni parametriche:

$$
\begin{cases}
x = t \\
y = 0 \\
z = 1 - t^{2}
\end{cases}
$$

In questo modo, la curva si può facilmente rappresentare su Geogebra usando il comando Curve

Curve(t, 0, 1 - t^2, t, -5, 5)

E così via.