Cilindro
Il cilindro è un solido ottenuto dalla rotazione completa di un rettangolo intorno a una retta (detta "asse") passante per uno dei suoi lati.
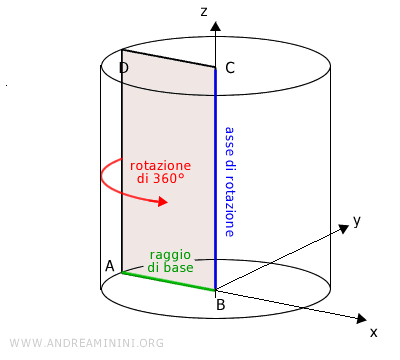
Pertanto, il cilindro è un solido di rotazione.
La distanza tra l'asse e il lato opposto del rettangolo è detta "raggio di base" o "raggio del cilidro".
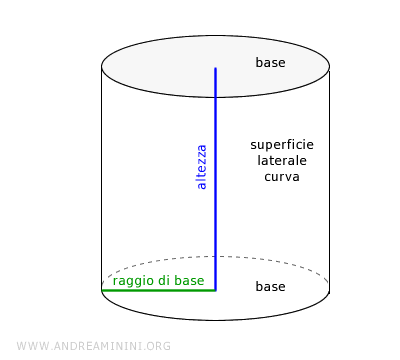
Il cilindro è delimitato da due superfici circolari dette "basi" e da una superficie laterale curva.
L'altezza del cilindro è la distanza tra le due basi. E' il lato attorno al quale ruota il cilindro ed è perpendicolare alle basi.
Quando l'altezza del cilindro coincide con il diametro della base, il cilindro è detto cilindro equilatero.
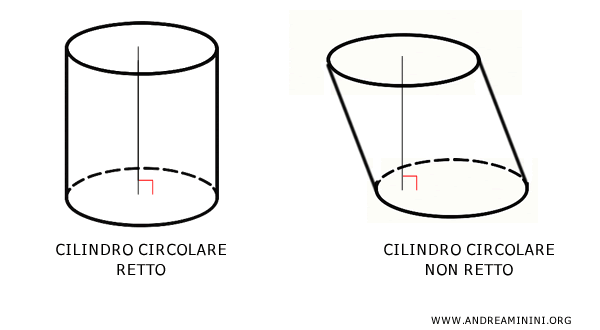
Nota. Quando si parla di "cilindro" nella geometria elementare si intende generalmente il "cilindro circolare retto". Oltre a questo esistono anche altri tipi di cilindri detti "cilindri indefiniti". Ad esempio, il cilindro ellittico, il cilindro parabolico, il cilindro iperbolico e altre tipologie di cilindri circolari non retti (es. cilindro obliquo) che non sono ottenibili tramite una semplice rotazione completa di un rettangolo. In questo caso l'altezza del cilindro non coincide con l'asse di rotazione.
Formule
Alcune formule per calcolare le grandezze del cilindro circolare retto
- Superficie di base
E' l'area di base del cilindro e si calcola come l'area di un cerchio. $$ S_B = \pi r^2 $$ - Superficie laterale
È l'area della superficie laterale del cilindro e si calcola come il prodotto della circonferenza di base (perimetro) per l'altezza del cilindro (h).Per un cilindro circolare retto, la formula è:
$$ S_L = 2 \pi r \cdot h $$ Dove r è il raggio di base, π è la costante pi greco (circa 3.14159). - Superficie totale
È la somma dell'area laterale e dell'area delle due basi. Poiché le basi di un cilindro circolare retto sono cerchi, l'area di ciascuna base è 2πr. Quindi, la formula per l'area totale è la seguente:
$$ S_T = S_L + 2 \cdot \pi r^2 $$ $$ S_T = 2 \pi r \cdot h + 2 \cdot \pi r^2 $$ $$ S_T = 2 \pi r \cdot (h+r) $$Spiegazione. Per capire meglio il senso della formula, sviluppo il cilindro sul piano.
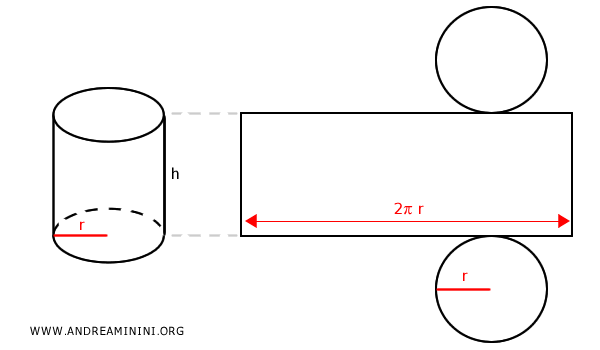
La superficie laterale del cilindro è un rettangolo che ha per base la circonferenza rettificata (2πr) e per altezza la stessa altezza del cilindro (h). $$ S_L = 2 \pi r \cdot h $$ Sapendo che l'area della superficie di base è quella di un cerchio. $$ S_B = \pi r^2 $$ Quindi, l'area totale del cilindro è la somma delle due superfici di base e dell'area laterale. $$ S_T = 2 S_B + S_L $$ $$ S_T = 2 ( \pi r^2 ) + 2 \pi r \cdot h $$ $$ S_T = 2 \pi r^2 + 2 \pi r h $$ $$ S_T = 2 \pi r \cdot ( r + h ) $$ E' esattamente la formula che volevo dimostrare. - Volume
Il volume V di un cilindro circolare retto è dato dal prodotto dell'area della base per l'altezza h del cilindro. Per una base circolare con raggio r, l'area della base è A=πr2. Quindi, la formula per calcolare il volume del cilindro è: $$ V = \pi r^2 \cdot h $$ Questa formula vale per qualsiasi cilindro circolare retto, indipendentemente dal fatto che sia obliquo o no, poiché il volume dipende solo dall'area della base e dall'altezza perpendicolare alle basi.Nota. In base al teorema di equivalenza del volume di un cilindro e un prisma, posso scrivere $$ V = A \cdot h = \pi r^2 h $$
Tipi di cilindri
Esistono varie tipologie di cilindri.
- Cilindro circolare retto
Ha basi circolari e la superficie laterale perpendicolare alle basi. L'altezza del cilindro coincide con l'asse di rotazione. - Cilindro circolare non retto
Ha le basi circolari, come il precedente, ma la superficie laterale non è perpendicolare alle basi. Può essere inclinato (cilindro obliquo) o presentare curve o torsioni. - Cilindro obliquo
Se le linee generatrici sono inclinate rispetto alle basi, allora il cilindro è obliquo. In questo caso, la sezione trasversale non è un rettangolo. - Cilindro ellittico
Ha basi ellittiche anziché circolari. - Cilindro parabolico
Non è limitato da basi e si estende all'infinito in una direzione, con una sezione trasversale che forma una parabola. - Cilindro iperbolico
Simile al parabolico, ma con una sezione trasversale che forma un'iperbole.
Questi sono solo alcuni esempi di cilindri "indefiniti" o non retti, e ci sono molte altre forme cilindriche possibili a seconda delle curve delle basi e della natura delle superfici laterali.
Cilindro nella geometria analitica
La nozione di cilindro si estende anche alla geometria analitica e può essere rappresentata mediante equazioni in coordinate cartesiane, cilindriche o sferiche.
Un cilindro circolare retto con l'asse lungo l'asse z e il centro della base situato all'origine ha l'equazione
$$ x^2+y^2=r^2 $$
Dove r è il raggio delle basi circolari.
Questa equazione descrive tutti i punti (x,y,z) la cui distanza dall'asse z è costantemente uguale a r.
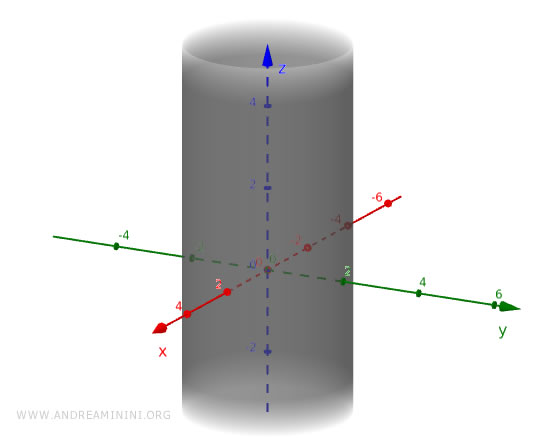
Poiché quest'area si estende all'infinito, per ottenere un cilindro devo anche indicare un intervallo per i valori dell'asse z.
Ad esempio, se il cilindro si estende dall'origine del piano (0;0;0) verso l'alto fino a un'altezza h, l'intervallo di z è il seguente:
$$ 0 \le z \le h $$
Il risultato è un cilindro con un'altezza finita con una base sul piano cartesiano xy.
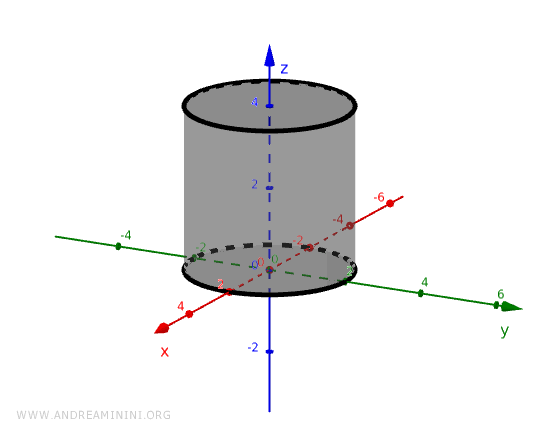
Cilindro circolare
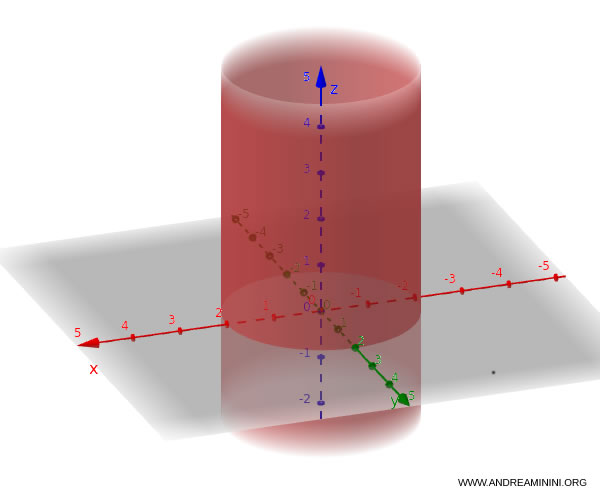
L'equazione di un cilindro indefinito circolare è $$ x^2 + y^2 + a x + b y + c = 0 $$
Questa equazione descrive una superficie cilindrica circolare se e solo se la curva direttrice sul piano $xy$ rappresenta effettivamente una circonferenza, ovvero se soddisfa la seguente condizione:
$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
Si parla di cilindro "indefinito" perché il cilindro non ha una altezza finita, si estende all’infinito in entrambe le direzioni lungo l’asse delle generatrici.
Dimostrazione. Considero l'equazione $$ x^2 + a x + y^2 + b y + c = 0 $$ Raggruppo i termini con la $ x $ e la $ y $. $$ (x^2 + a x) + (y^2 + b y) + c = 0 $$ Ora completo il quadrato. Aggiungo e sottraggo $ \frac{a^2}{2^2} $ e $ \frac{b^2}{2^2} $ $$ (x^2 + a x + \frac{a^2}{2^2} - \frac{a^2}{2^2}) + (y^2 + b y + \frac{b^2}{2^2} - \frac{b^2}{2^2}) + c = 0 $$ $$ (x^2 + a x + \frac{a^2}{2^2} ) + (y^2 + b y + \frac{b^2}{2^2} ) + c - \frac{a^2}{2^2} - \frac{b^2}{2^2} = 0 $$ $$ (x^2 + a x + ( \frac{a}{2} )^2 ) + (y^2 + b y + ( \frac{b}{2} )^2 ) = \frac{a^2}{2^2} + \frac{b^2}{2^2} -c $$ Completando il quadrato diventa $$ \left( x + \frac{a}{2} \right)^2 + \left( y + \frac{b}{2} \right)^2 = \frac{a^2}{2^2} + \frac{b^2}{2^2} -c $$ $$ \left( x + \frac{a}{2} \right)^2 + \left( y + \frac{b}{2} \right)^2 = \frac{a^2}{4} + \frac{b^2}{4} - c $$ Affinché ci sia una circonferenza reale, il termine a destra dev’essere positivo o nullo (raggio reale e non immaginario): $$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
Lo stesso principio vale anche per gli altri piani:
- Nel piano xz l'equazione in $x$ e $z$ è: $$ x^2 + z^2 + a x + b z + c = 0 $$ In questo caso il cilindro è circolare con asse parallelo a $y$.
- Nel piano yz l'equazione in $y$ e $z$ è: $$ y^2 + z^2 + a y + b z + c = 0 $$ In questo caso il cilindro è circolare con asse parallelo a $x$.
Esempio
Ecco un esempio di cilindro indefinito circolare
$$ \frac{x^2}{4} + \frac{y^2}{4} = 1 $$
Questa equazione descrive una superficie cilindrica circolare.
Cilindro ellittico
L’equazione cartesiana di un cilindro ellittico indefinito con asse parallelo all’asse z è: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Un cilindro indefinito ellittico è una superficie tridimensionale generata traslando un’ellisse lungo una direzione parallela a un asse dello spazio, solitamente l’asse z.
Questa relazione descrive l’insieme di tutti i punti $(x, y, z)$ tali che la loro proiezione sul piano xy appartenga all’ellisse di equazione:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Il valore di $z$ può essere qualsiasi numero reale.
Nota. Se i coefficienti sono uguali ($a = b = r$), l’equazione diventa: $$ \frac{x^2}{r^2} + \frac{y^2}{r^2} = 1 $$ cioè: $$ x^2 + y^2 = r^2 $$ In questo caso, la sezione del cilindro sul piano xy è un cerchio di raggio $r$. Il cilindro diventa un cilindro circolare.
Esempio
Considero il seguente cilindro:
$$ \frac{x^2}{4} + \frac{y^2}{9} = 1 $$
La variabile $z$ non compare nell’equazione, quindi il cilindro si estende all’infinito lungo l’asse z.
Sul piano xy, il cilindro ha forma ellittica:
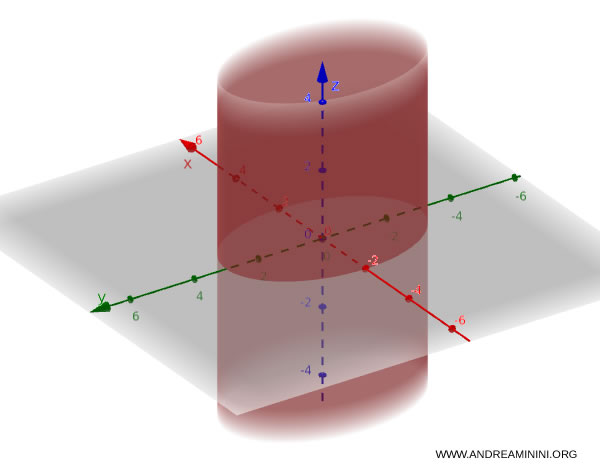
Si presenta come una superficie rigata, ossia composta da rette parallele (generatrici) tutte dirette lungo l’asse $z$, e senza una altezza definita.
In questo caso i semiasse dell'ellisse sono
- $a = 2$ (lunghezza semiasse sull’asse x)
- $b = 3$ (lunghezza semiasse sull’asse y)
La sezione del cilindro sul piano xy è un’ellisse con i semiassi $a$ e $b$ data dall’equazione di base.
Cilindro iperbolico
Un cilindro iperbolico è una superficie tridimensionale generata traslando un’iperbole lungo una direzione parallela a un asse cartesiano. La sua equazione generale è:$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$ Questa relazione descrive una superficie per ogni valore di $z$.
In altre parole, qualunque sia la quota $z$, i punti $(x, y)$ appartengono sempre alla stessa iperbole sul piano $xy$.
La superficie del cilindro iperbolico è composta da due elementi fondamentali:
- Direttrice: è l’iperbole definita nel piano $xy$ dall’equazione $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$. Questa curva ha due rami aperti verso l’esterno, separati dagli asintoti.
- Generatrici: sono rette parallele all’asse $z$. Spostando l’iperbole lungo queste rette, si ottiene la superficie tridimensionale del cilindro iperbolico.
Quindi, il cilindro iperbolico è una superficie rigata, perché composta da infinite rette generatrici, ed è una superficie cilindrica perché la sua sezione con piani paralleli al piano $xy$ è sempre la stessa iperbole.
L’asse lungo il quale si sviluppano le generatrici definisce l’orientamento del cilindro. Nell’equazione $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ l’asse è parallelo all’asse $z$.
Cambiando l'asse $ z $ con l'asse $ x $ o $ y $ si ottiene un orientamento diverso del cilindro iperbolico.
Esempio. Consideriamo l’equazione: $$ \frac{x^2}{2} - \frac{y^2}{4} = 3 $$ In questo caso la direttrice si trova sul piano $xy$, la curva è un’iperbole aperta lungo l’asse $x$. L’equazione della direttrice si riscrive così: $$ x^2 = 2 \left( 3 + \frac{y^2}{4} \right ) $$ oppure: $$ y^2 = 4 \left( \frac{x^2}{2} - 3 \right ) $$ Le rette generatrici sono le rette parallele all’asse $z$. Questo significa che per ogni punto $(x, y)$ sull’iperbole, esiste una retta verticale che si estende indefinitamente lungo $z$.
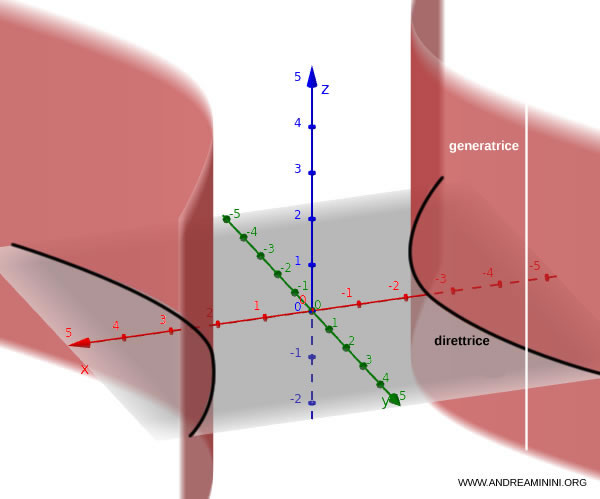
Cilindro parabolico
Il cilindro parabolico è una superficie tridimensionale generata traslando una parabola lungo una direzione parallela a uno degli assi cartesiani. L’equazione generale è:$$ y = k x^2 $$ dove $k$ è un coefficiente reale. In questo caso, l’asse del cilindro parabolico è parallelo all’asse $z$
Se questa relazione vale per ogni valore di $z$, allora la superficie si estende indefinitamente lungo l’asse $z$ e il cilindro è detto "indefinito" poiché non ha un'altezza ben definita.
Esempio. Considero la direttrice $ y = x^2 $ ossia una parabola. La superficie corrispondente è $$y = x^2, \quad z \in \mathbb{R} $$Questa superficie è costituita da infinite parabole identiche nel piano $x\text{-}y$, ripetute lungo l’asse $z$.
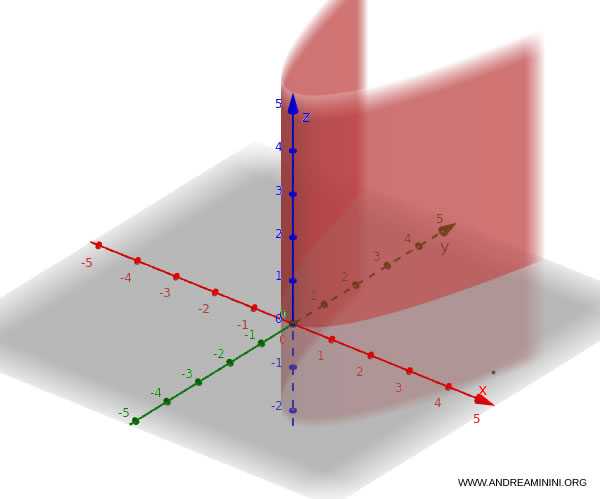
E' come avere una parabola sul piano $ xy $ e spostarla in alto e in basso in una direzione parallela all'asse z.
Se la parabola si trova nel piano $x\text{-}z$, l’equazione diventa:
$$ z = x^2 $$
In questo caso il cilindro parabolico ha l’asse parallelo all’asse $y$, perché la variabile $y$ può assumere qualsiasi valore.
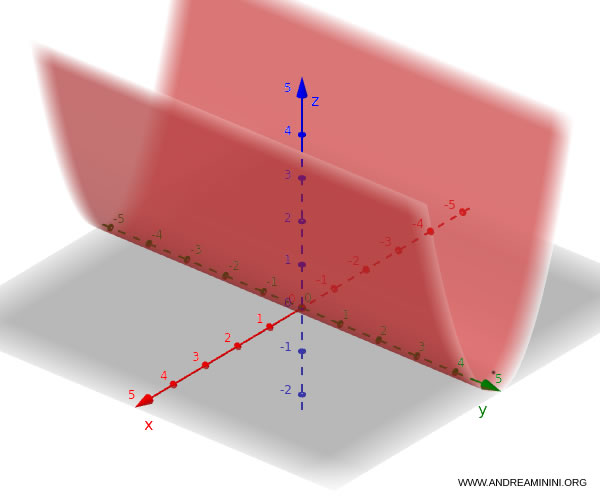
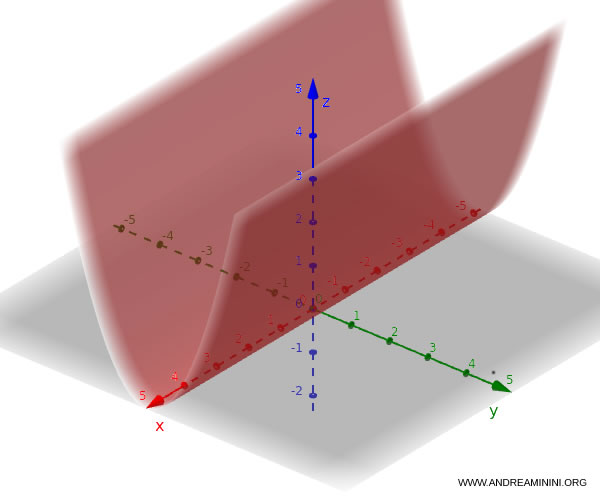
Analogamente, se la parabola si trova nel piano $y\text{-}z$, l’equazione è:
$$ z = y^2 $$
Questa volta l’asse del cilindro parabolico è parallelo all’asse $x$.
Osservazioni
Alcune osservazioni e note sui cilindri
- Due cilindri circolari retti sono congruenti se hanno la stessa altezza e lo stesso raggio di base.
- Se si seziona un cilindro circolare retto con un piano passante per l'asse di rotazione e perpendicolare alla base, si ottiene un rettangolo oppure un quadrato nel caso in cui il cilindro è anche equilatero.
- Il cilindro è simile a un prisma con una base poligonale, ma poiché ha basi circolari, ha proprietà uniche, come la simmetria rotazionale attorno al suo asse.
- Equivalenza in volume tra prisma e cilindro
Un cilindro e un prisma (di qualsiasi forma di base) che hanno la stessa area di base $A$ e la stessa altezza $h$ hanno lo stesso volume.
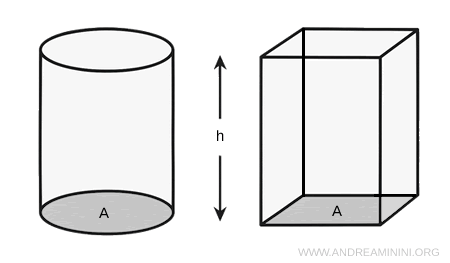
Dimostrazione. In entrambi i casi la formula del volume è: $$ V = A \cdot h $$ dove $A$ è l’area della base, $h$ è l’altezza (la distanza perpendicolare tra le due basi).
E così via
