Simmetria assiale
La simmetria assiale (o riflessione) è una trasformazione isometrica in cui ogni punto di una figura viene riflesso in un punto corrispondente alla stessa distanza sull'altro lato di una retta, detta asse di simmetria.
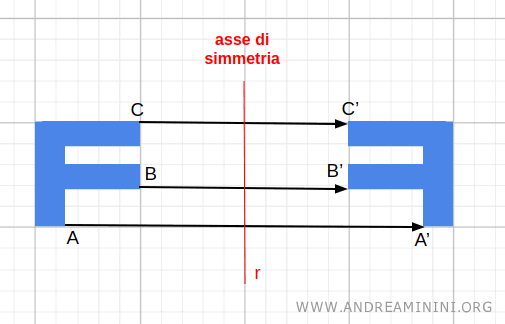
In pratica la simmetria assiale divide il piano in due parti tramite una retta r detta asse di simmetria.
Ogni punto A su un lato della retta ha un corrispondente punto A' sull'altro lato.
La linea che unisce questi due punti, AA', è sempre perpendicolare alla retta r e il suo punto medio si trova sull'asse di simmetria.
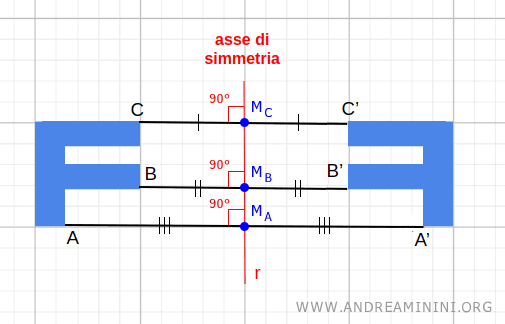
Per questa ragione si chiama "assiale", la retta r è l'asse del segmento che unisce i due punti AA'.
- r è perpendicolare al segmento AA'
- r passa per il punto medio del segmento AA'
Nota. La simmetria assiale è una isometria perché la figura viene riflessa da un semipiano all'altro senza modificare la forma, la dimensione e la distanza tra i punti. Le due figure nei semipiani sono congruenti tra loro.
Un esempio pratico
Ad esempio, la figura nel semipiano a sinistra viene riflessa sul semipiano a destra, in modo perpendicolare e alla stessa distanza dall'asse di simmetria r.

Il punto C viene riflesso sul semipiano a destra nel punto C'.
Sia il punto C che il punto C' si trovano a una distanza pari a 5 dall'asse di simmetria.
Il segmento CC' che unisce i due punti ha il suo punto medio sull'asse di simmetria r.
La definizione formale di simmetria assiale
Fissata una retta r nel piano la simmetria assiale è una trasformazione geometrica che fa corrispondere:
- ogni punto R della retta r con se stesso
- ogni punto P non appartenente alla retta r con un punto P' tale che:
- i punti P e P' hanno la stessa distanza dalla retta r
- il segmento PP' è perpendicolare alla retta r
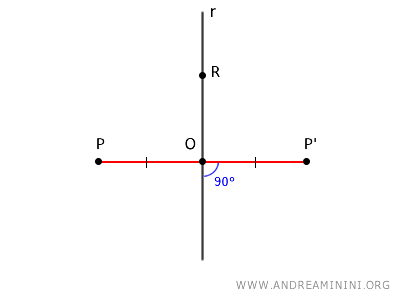
La retta r è detta asse di simmetria.
Pertanto, i segmenti OP e OP' sono congruenti.
$$ \overline{OP} \cong \overline{OP'} $$
Tutti i punti R sulla retta r, invece, sono degli invarianti della trasformazione geometrica, perché la posizione di questi punti non cambia dopo la simmetria assiale.
In altre parole, tutti i punti R dell'asse di simmetria assiale sono dei punti uniti della trasformazione geometrica.
Tipi di simmetrie assiali
Esistono due principali tipi di simmetrie assiali
- La riflessione
E' una simmetria assiale che si verifica sul piano, ossia in uno spazio a due dimensioni. - Il ribaltamento
E' una simmetria assiale nello spazio, ossia in uno spazio a tre dimensioni.
Le simmetrie assiali notevoli nella geometria analitica
Alcune simmetrie assiali sono dette "notevoli" perché riguardano gli assi cartesiani del piano, le bisettrici o le rette parallele agli assi del piano.
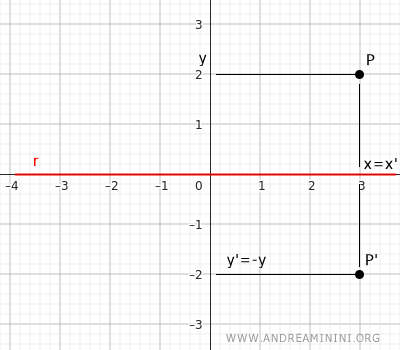
- La simmetria rispetto all'asse dell'ascisse
In questo caso l'asse di simmetria assiale è l'asse x. Per calcolare le coordinate del punto corrispondente P'(x';y') di un punto P(x;y) posso usare queste equazioni. $$ \begin{cases} x' = x \\ \\ y' = -y \end{cases} $$ Due punti simmetrici rispetto all'asse x hanno ordinate opposte e la stessa ascissa.
Esempio. La componente x delle coordinate cartesiane è costante mentre la componente delle ordinate y'=-y è opposta.
- La simmetria rispetto all'asse delle ordinate
L'asse di simmetria assiale è l'asse y del piano cartesiano. Per calcolare le coordinate del punto corrispondente P'(x';y') di un punto P(x;y) si utilizzano queste equazioni. $$ \begin{cases} x' = -x \\ \\ y' = y \end{cases} $$ Due punti simmetrici rispetto all'asse y hanno ascisse opposte e la stessa ordinata.
Esempio. In questo caso la componente y delle coordinate cartesiane resta la stessa mentre la componente x è opposta.
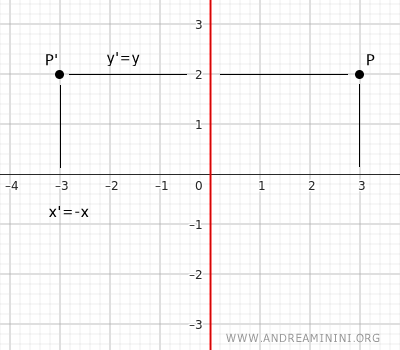
- La simmetria rispetto a una parallela all'asse dell'ascisse
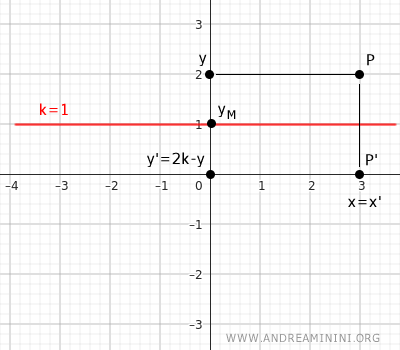
Si considera come asse di simmetria una retta y=k parallela all'asse delle ascisse x. Le equazioni della trasformazione isometrica sono le seguenti: $$ \begin{cases} x' = x \\ \\ y' = 2k-y \end{cases} $$
Dimostrazione. In questo caso la coordinata delle ascisse x'=x è costante. La componente delle ordinate y' è invece differente. Il punto medio yM del segmento PP rispetto alle coordinate y è uguale alla media delle due componenti y e y' $$ k = \frac{y+y'}{2} $$ Da questa equazione ricavo l'ordinata y' $$ y' = 2k - y $$ Ecco un esempio pratico.
- La simmetria rispetto a una parallela all'asse delle ordinate
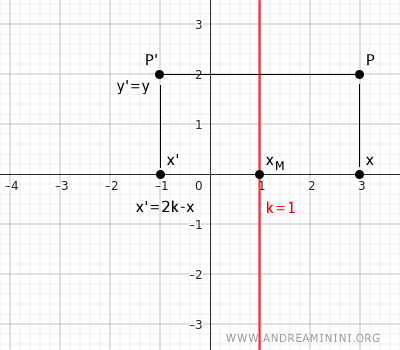
In questo caso l'asse di simmetria è una retta x=k parallela all'asse delle ordinate y. Le equazioni della trasformazione isometrica sono le seguenti: $$ \begin{cases} x' = 2k-x \\ \\ y' = y \end{cases} $$Dimostrazione. In questo caso la coordinata y' è la stessa. La componente x è invece diversa. Il punto medio M del segmento PP è uguale alla media dei due punti $$ k = \frac{x+x'}{2} $$ Da questo ottengo l'equazione che determina l'ascissa x' $$ x' = 2k - x $$ Ecco un esempio pratico.
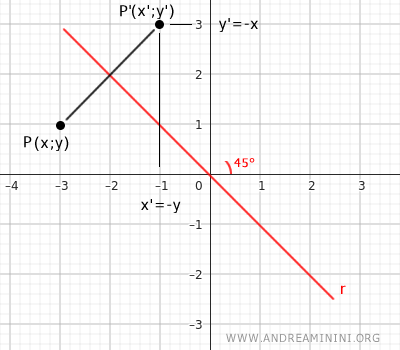
- La simmetria rispetto alla bisettrice dei quadranti
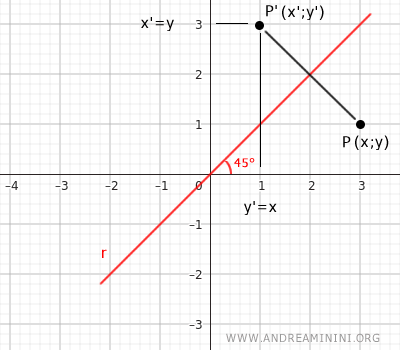
L'asse di simmetria è la bisettrice dei quadranti. Se la bisettrice si trova nel I e III quadrante del piano cartesiano, le equazioni della trasformazione assiale sono le seguenti: $$ \begin{cases} x' = y \\ \\ y' = x \end{cases} $$ Viceversa, se la bisettrice si trova nel II e IV quadrante, le equazioni della trasformazione sono le seguenti: $$ \begin{cases} x' = -y \\ \\ y' = -x \end{cases} $$Esempio. Ecco un esempio di simmetria assiale rispetto alla bisettrice del quadrante I. Le componenti delle coordinate si invertono x'=y e y'=x.
Quest'altro esempio, invece, riguarda una simmetria assiale rispetto alla bisettrice del quadrante II. Ogni componente delle coordinate è l'opposto dell'altra componente ossia x'=-y e y'=-x.
- Simmetria rispetto alla retta (y = mx + q)
Per trovare il simmetrico $P'(x', y')$ di un punto $P(x, y)$ rispetto a una generica retta $r$ di equazione $ y = mx + q $ occorre soddisfare due condizioni fondamentali:- Perpendicolarità
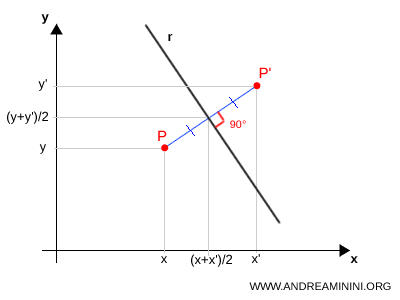 Il segmento $PP'$ deve essere perpendicolare alla retta $r$. Di conseguenza, il coefficiente angolare di $PP'$ è l’opposto del reciproco di $m$: $$ \frac{y' - y}{x' - x} = -\frac{1}{m} $$
Il segmento $PP'$ deve essere perpendicolare alla retta $r$. Di conseguenza, il coefficiente angolare di $PP'$ è l’opposto del reciproco di $m$: $$ \frac{y' - y}{x' - x} = -\frac{1}{m} $$ - Equidistanza
Il punto medio del segmento $PP'$ deve appartenere alla retta $r$. In altre parole, il punto $$ M\!\left(\frac{x+x'}{2}, \; \frac{y+y'}{2}\right) $$ si trova su $r$, quindi: $$ \frac{y+y'}{2} = m \cdot \frac{x+x'}{2} + q $$
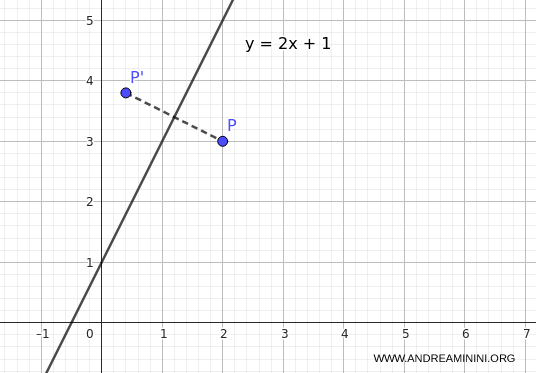
Esempio. Devo trovare il simmetrico del punto $P(2,3)$ rispetto alla retta $ r: \; y = 2x + 1 $. Per farlo utilizzo le formule di trasformazione $$ \begin{cases} x' = \frac{(1-m^2)x + 2my - 2mq}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx + 2q}{m^2+1} \end{cases} $$ Sostituisco $m=2, q=1, x=2, y=3$: $$ \begin{cases} x' = \frac{(1-4)\cdot 2 + 2\cdot 2\cdot 3 - 2\cdot 2\cdot 1}{2^2+1} \\ \\ y' = \frac{(4-1)\cdot 3 + 2\cdot 2\cdot 2 + 2\cdot 1}{5} \end{cases} $$ $$ \begin{cases}
x' = \frac{-6 + 12 - 4}{5} = \frac{2}{5} = 0.4 \\ \\ y' = \frac{9 + 8 + 2}{5} = \frac{19}{5} = 3.8 \end{cases} $$ Quindi, il punto simmetrico di $ P $ rispetto alla retta $ r $ è $ P'(0.4,\;3.8) $.
- Perpendicolarità
- Simmetria rispetto alla retta (y = mx)
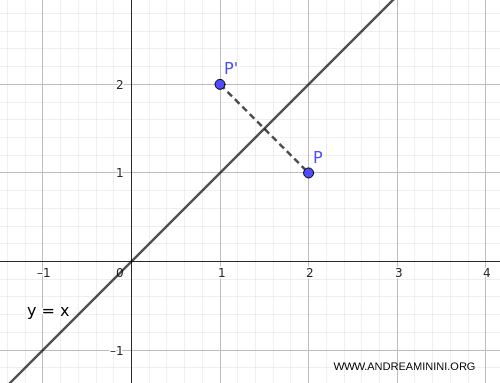
Se l’asse di simmetria è la retta $ y = m x $ passante per l’origine, in alternativa posso usare anche la seguente formula per ottenere le coordinate del punto simmetrico $(x',y')$ del punto $(x,y)$: $$ \begin{cases} x' = x \cos 2\alpha + y \sin 2\alpha \\[6pt] y' = x \sin 2\alpha - y \cos 2\alpha \end{cases} $$ Dove $\alpha = \arctan(m)$ è l’angolo che la retta $y=mx$ forma con l’asse $x$.Esempio. Devo trovare il simmetrico del punto $(2,1)$ rispetto alla retta $y=x$. In questo caso la retta $y=x$ ha coefficiente angolare $m=1$. Quindi, l'angolo in radianti è $\alpha = \arctan(1) = \tfrac{\pi}{4}$. Calcoliamo i doppi angoli:$$ \cos 2\alpha = \cos \tfrac{\pi}{2} = 0 $$ $$ \sin 2\alpha = \sin \tfrac{\pi}{2} = 1 $$ Poi applico la formula: $$ \begin{cases} x' = 2 \cdot 0 + 1 \cdot 1 = 1 \\[6pt] y' = 2 \cdot 1 - 1 \cdot 0 = 2 \end{cases} $$ Quindi il punto simmetrico di $(2,1)$ rispetto alla retta $y=x$ è $ (x',y') = (1,2)$
Dimostrazione. Per dimostrare la formula parto dal sistema di equazioni della simmetria assiale rispetto a una retta $ y=mx+q $ $$ \begin{cases} x' = \frac{(1-m^2)x + 2my - 2mq}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx + 2q}{m^2+1} \end{cases} $$ Se la retta passa per l'origine $ y = mx $ il termine noto è nullo $ q=0 $ $$ \begin{cases} x' = \frac{(1-m^2)x + 2my}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx}{m^2+1} \end{cases} $$ Sapendo che il coefficiente angolare di una retta è $ m = \tan \alpha $ sostituisco $ m $ nelle equazioni. $$ \begin{cases} x' = \frac{(1-\tan^2 \alpha)x + (2 \tan \alpha)y}{\tan^2 \alpha +1} \\ \\ y' = \frac{(\tan^2 \alpha -1)y + (2 \tan \alpha)x}{\tan^2 \alpha+1} \end{cases} $$ $$ \begin{cases} x'= \frac{(1-\tan^2 \alpha) x + (2 \tan \alpha)y}{\tan^2 \alpha +1} \\ \\ y' = \frac{(\tan^2 \alpha -1)y + (2 \tan \alpha)x}{\tan^2 \alpha+1} \end{cases} $$ $$ \begin{cases} x'= \frac{1-\tan^2 \alpha }{1+\tan^2 \alpha } x + \frac{2 \tan \alpha}{1+\tan^2 \alpha } y \\ \\ y' = \frac{\tan^2 \alpha -1}{1+\tan^2 \alpha}y + \frac{2 \tan \alpha}{1+\tan^2 \alpha}x \end{cases} $$ $$ \begin{cases} x'= \frac{1-\tan^2 \alpha }{1+\tan^2 \alpha } x + \frac{2 \tan \alpha}{1+\tan^2 \alpha } y \\ \\ y' = \frac{2 \tan \alpha}{1+\tan^2 \alpha}x - \frac{1-\tan^2 \alpha}{1+\tan^2 \alpha}y \end{cases} $$ A questo punto sostituisco le formule parametriche della trigonometria $ \cos 2 \alpha = \frac{1- \tan^2 \alpha}{1 + \tan^2 \alpha} $ e $ \sin 2 \alpha = \frac{2 \tan \alpha}{1 + \tan^2 \alpha} $. $$ \begin{cases} x'= x \cos 2 \alpha + y \sin 2 \alpha \\ \\ y' = x \sin 2 \alpha - y \cos 2 \alpha \end{cases} $$ Ho così dimostrato la formula.
Questi sono i casi più frequenti di simmetria assiale.
E' comunque possibile calcolare la riflessione rispetto a una retta con qualsiasi angolazione. In questi casi è però necessario utilizzare la matrice di riflessione. Ne parlo del prossimo paragrafo.
La matrice di riflessione
Nel piano la riflessione rispetto a una retta y=mx (asse di simmetria) passante per l'origine del piano cartesiano può essere ottenuta utilizzando la matrice di riflessione.
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = A \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$
Dove (x;y) sono le coordinate iniziali di un punto P, mentre (x';y') sono le coordinate del punto corrispondente P' dopo la simmetria assiale.
La matrice di riflessione è la seguente
$$ A = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} $$
Il termine α è l'ampiezza dell'angolo che la retta y=mx forma rispetto all'asse positivo delle ascisse (x)
Nota. L'angolo α si può ottenere tramite l'arcotangente del coefficiente angolare (m) della retta y=mx. Sapendo che m=y/x. $$ \alpha = \arctan(m) $$ Va però sottolineato che la formula α=arctan(m) non funziona quando la retta r è perfettamente perpendicolare all'asse delle ascisse (90° o 270°), perché in questo caso il coefficiente angolare tende a infinito.
Per comprendere meglio come si utilizza, è utile fare un esempio pratico.
Esempio
Ad esempio, considero il punto alle coordinate x=2 e y=3
$$ P = (2;3) $$
Rappresento il punto sul diagramma cartesiano
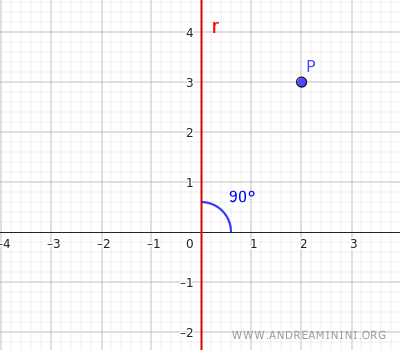
Utilizzo per semplicità una retta y=mx che forma un angolo di 90° (π/2 radianti) rispetto al semiasse positivo delle x.
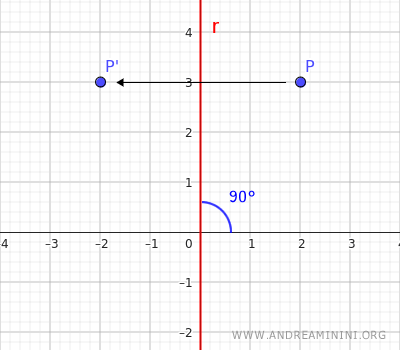
Calcolo le nuove coordinate tramite la matrice di riflessione
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$
Le coordinate iniziali del punto sono P=(2;3) ossia x=2 e y=3
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
In questo esempio l'angolo α=90° ha un'ampiezza di novanta gradi (π/2 radianti)
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \cdot 90°) & \sin ( 2 \cdot 90° ) \\ \sin ( 2 \cdot 90°) & - \cos(2 \cdot 90°) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (180°) & \sin ( 180° ) \\ \sin (180°) & - \cos(180°) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
Sapendo che il seno di 180 è uguale a 0, mentre il coseno di 180° è uguale a -1
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & - (-1) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 \cdot 2 + 0 \cdot 3 \\ 0 \cdot 2 + 1 \cdot 3 \end{pmatrix} $$
Il risultato finale sono le coordinate del punto corrispondente.
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} $$
Le nuove coordinate del punto P'=(-2;3) dopo la riflessione assiale sono x=-2 e y=3.
L'asimmetria assiale nello spazio con i solidi
La simmetria assiale nello spazio è una trasformazione geometrica che riflette un solido rispetto a un asse assegnato.
Si tratta di una isometria, cioè una trasformazione che conserva dimensioni e forme del solido trasformato.

Data una retta \( r \) nello spazio tridimensionale, la simmetria assiale rispetto a \( r \) è la trasformazione che:
- Mantiene invariati tutti i punti appartenenti alla retta \( r \) (punti uniti).
- Trasforma ogni altro punto \( P \) in un punto \( P' \), tale che:
- Il segmento \( PP' \) è perpendicolare all'asse \( r \).
- I punti \( P \) e \( P' \) sono equidistanti da \( r \). Quindi, i segmenti \( OP \cong OP' \) sono congruenti, dove \( O \) è il punto in cui il segmento \( PP' \) interseca la retta \( r \).
Quali sono le proprietà della simmetria assiale nello spazio?
L'asimmetria assiale conserva le distanze tra i punti. Quindi, due punti che erano a distanza \( d \) prima della simmetria rimangono alla stessa distanza \( d \) anche dopo la trasformazione.
Inoltre, mantiene il volume del solido riflesso, ne preserva la forma e non cambia gli angoli interni tra le facce del solido.
Quindi, un solido simmetrico è congruente a quello originale.
La simmetria rispetto a un piano
La simmetria rispetto a un piano è una generalizzazione della simmetria assiale nello spazio tridimensionale, nel senso che la simmetria assiale si basa su una retta, mentre quella planare si basa su un piano.
Nel caso della simmetria rispetto a un piano un punto e il suo simmetrico sono equidistanti dal piano e sono allineati lungo una retta perpendicolare al piano stesso.
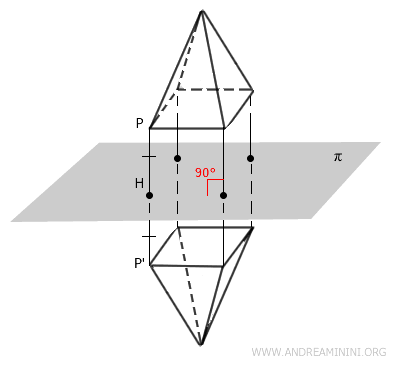
Quindi, data una figura solida nello spazio tridimensionale e un piano di simmetria \( \pi \):
- Ogni punto appartenente al piano \( \pi \) resta invariato (è un punto unito).
- Ogni punto \( P \) non appartenente a \( \pi \) viene trasformato in un punto \( P' \), tale che:
- La retta \( PP' \) è perpendicolare al piano \( \pi \).
- I segmenti \( PH \) e \( P'H \), dove \( H \) è la proiezione ortogonale di \( P \) su \( \pi \), sono uguali in lunghezza ( \( PH \cong P'H \) ).
Il piano \( \pi \) è quindi il piano di simmetria.
Nota. Anche in questa trasformazione geometrica le figure trasformate mediante una simmetria rispetto a un piano sono inversamente congruenti: cioè, hanno le stesse dimensioni ma risultano specchiate. La trasformazione non altera distanze, angoli e proporzioni. Inoltre, se si applica due volte la simmetria rispetto allo stesso piano, si ritorna alla figura iniziale.
Osservazioni
Alcune osservazioni e note e margine sulle simmetrie assiali.
- La simmetria assiale è una isometria (dimostrazione)
Considero due punti $A$ e $B$ del piano e applico una simmetria assiale rispetto alla retta $r$, ottenendo i punti corrispondenti $A'$ e $B'$. Per definizione, i punti $A'$ e $B'$ si trovano alla stessa distanza dalla retta $r$; inoltre, le rette $AA'$ e $BB'$ sono perpendicolari a $r$, e i punti di intersezione $M_A$ e $M_B$ con la retta $r$ coincidono rispettivamente con i punti medi dei segmenti $AA'$ e $BB'$.
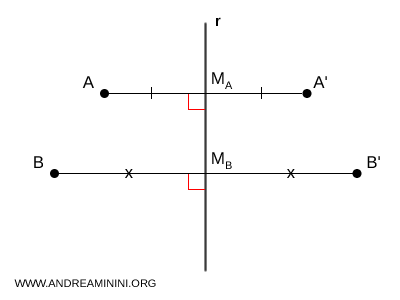
Le rette $AA'$ e $BB'$, per definizione di simmetria assiale, sono entrambe perpendicolari alla retta $r$ e quindi risultano parallele $ AA' \parallel BB' $. Di conseguenza, la distanza tra le due rette è costante in ogni loro punto. Sia $C$ la proiezione ortogonale di $A$ sulla retta $BB'$, e $C'$ quella di $A'$. Poiché $AA'$ e $BB'$ sono parallele, le proiezioni $AC$ e $A'C'$ sono perpendicolari a $BB'$ e quindi parallele e congruenti: $AC \cong A'C'$.
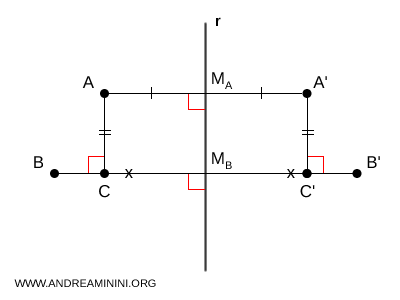
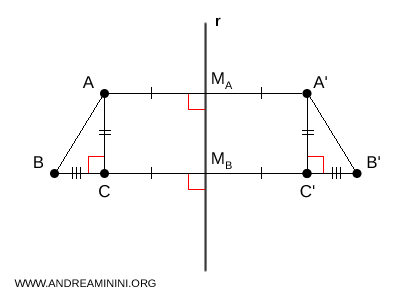
Quindi i segmenti $AM_A$ e $CM_B$ risultano congruenti, poiché rappresentano la distanza di punti simmetrici dalla retta $r$ e la simmetria assiale conserva tali distanze. Allo stesso modo, anche $A'M_A$ e $C'M_B$ sono congruenti. Ne consegue che i segmenti $BC$ e $B'C'$ sono anch’essi congruenti, $ BC \cong B'C' $, poiché ottenuti come differenza di segmenti congruenti ( $ BC = BM_B - CM_B $ e $ B'C' = B'M_B - C'M_B. $ ) Infine, da questo deduco che i segmenti $ AB \cong A'B' $ sono congruenti perché i triangoli $ ABC $ e $ A'B'C' $ sono due triangoli rettangoli congruenti $ ABC \cong A'B'C' $, in quanto hanno i cateti congruenti ( $ BC \cong B'C' $ e $ AC \cong A'C' $ ). Di conseguenza anche l'ipotenusa è congruente $ AB \cong A'B' $. Questo dimostra che la simmetria assiale ha conservato la distanza tra i punti .
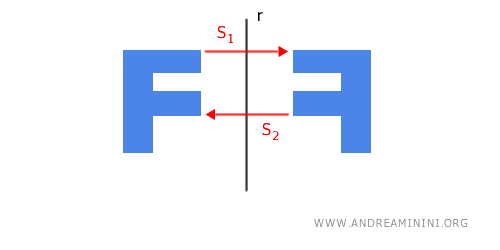
- La composizione di due simmetrie assiali con lo stesso asse di simmetria equivale a una identità
Se effettuo due volte (o un numero pari di volte) una simmetria assiale S1 e S2 con lo stesso asse di simmetria r su una figura, il risultato finale è la figura iniziale stessa, ovvero una identità perché la posizione dei punti della figura non cambia. Pertanto, una doppia simmetria assiale con lo stesso asse di simmetria è una trasformazione involutoria.
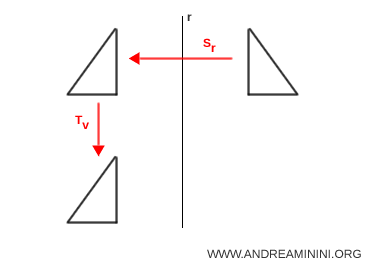
- La composizione di due simmetrie assiali con asse parallelo equivale a una traslazione
Se effettuo due volte una simmetria assiale S1 e S2 con due assi di simmetria r1 e r2 paralleli su una figura, il risultato finale è lo stesso che otterrei con una traslazione della figura iniziale.
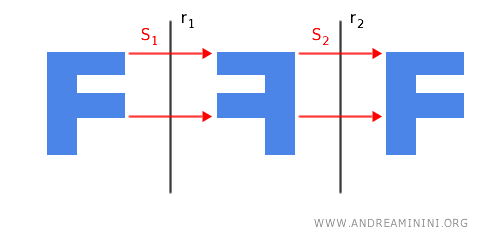
Nota. La traslazione di vettore $\vec{v}$ ha modulo pari al doppio della distanza ( $ d $ ) tra i due assi di simmetria $r_1$ e $r_2$, ed è perpendicolare a entrambi: $$ | \vec{v} | = 2d $$ Per dimostrarlo, basta osservare la figura.
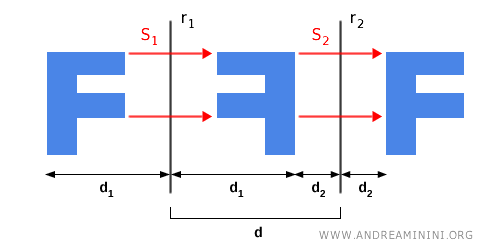
Sommando i singoli trasferimenti si ottiene: $$ | \vec{v} | = 2d_1 + 2d_2 = 2(d_1 + d_2) $$ Sapendo che la relazione $d_1 + d_2 = d$ è la distanza tra i due assi di simmetria, si ricava infine la formula da dimostrare $$ | \vec{v} | = 2(d_1 + d_2) = 2d $$ - La composizione di due simmetrie assiali con asse NON parallelo equivale a una rotazione
Se effettuo due volte una simmetria assiale S1 e S2 con due assi di simmetria r1 e r2 non paralleli su una figura, il risultato finale è lo stesso che otterrei con una rotazione della figura iniziale, con centro il punto O di intersezione tra i due assi di simmetria r1 e r2 e un angolo di rotazione con un'ampiezza congruente a 2α+2β ovvero al doppio dell'angolo γ formato dagli assi di simmetria (2γ).
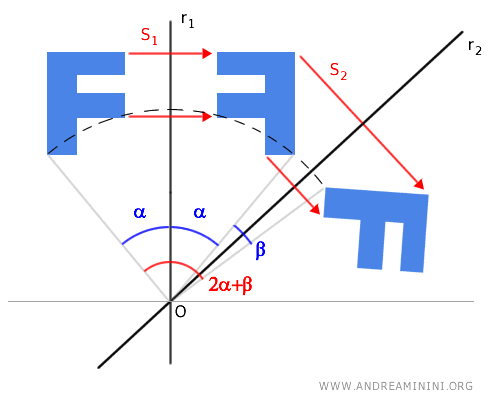
Poiché l'asse di simmetria r2 è la bisettrice dell'angolo 2β=β1+β2 con β1≅β2 deduco che α+β1≅α+β2 sono angoli congruenti. Chiamo l'angolo γ≅α+β1≅α+β2. Quest'ultimo angolo γ è congruente anche con l'angolo formato dagli assi di simmetria r1 e r2. Pertanto, posso ricavare molto più semplicemente l'angolo di rotazione come il doppio dell'angolo γ formato dagli assi di simmetria r1 e r2.
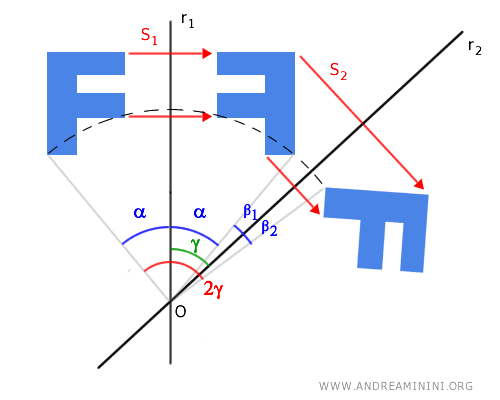
Nota. Quando gli assi di simmetria r1 e r2 sono perpendicolari, ossia formano un angolo retto (90°), la composizione di due simmetrie assiali equivale a una rotazione di 180° (angolo piatto).
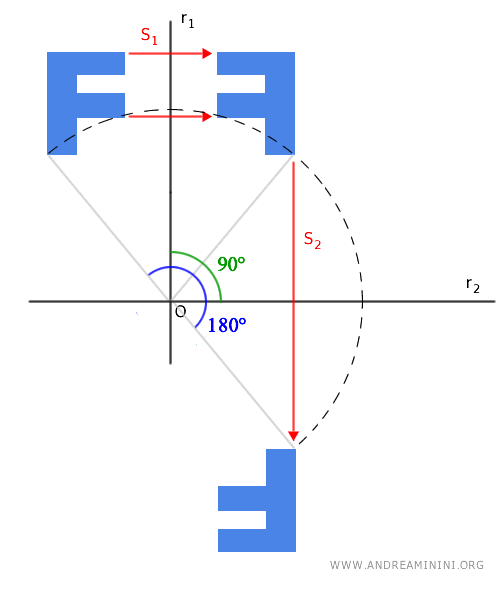
- Ogni isometria può essere espressa come una composizione di simmetrie assiali
Questa affermazione si basa su alcune proprietà fondamentali che ho già dimostrato in precedenza. In particolare, basta ricordarsi che:- Le rotazioni, le identità e le traslazioni possono essere rappresentate come composizioni di due specifiche simmetrie assiali.
- Le simmetrie centrali sono equivalenti a una rotazione di 180 gradi (angolo piatto) attorno allo stesso centro P.
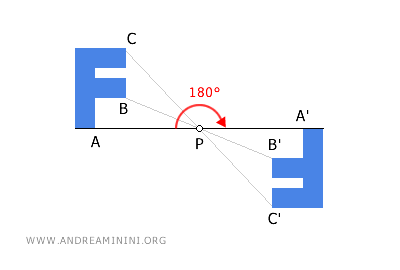
Sapendo che ogni rotazione può essere decomposta in simmetrie assiali, deduco che anche le simmetrie centrali possono essere ottenute tramite una composizione di simmetrie assiali.
- Figure unite nella simmetria assiale
Nella simmetria assiale l'asse di simmetria (r) è una figura unita perché non cambia. In particolar modo è una figura "puntualmente" unita perché ogni punto dell'asse non cambia le proprie coordinate.
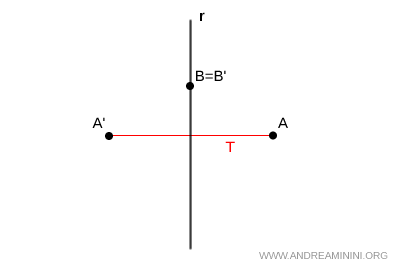
Anche ogni retta perpendicolare all'asse di simmetria è una figura unita. In questo caso però si parla di figura "globalmente" unita perché i punti cambiano le proprie coordinate dopo la trasformazione anche se la retta resta invariata.
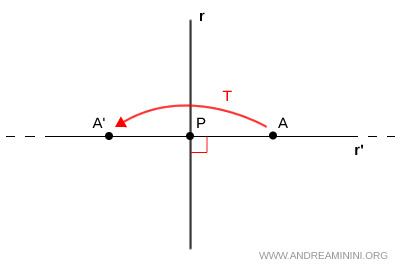
Nota. La retta $ r' $ è invariata dopo la trasformazione anche se i punti hanno cambiato coordinate. Ad esempio, l'immagine del punto A è il punto A'.
- Glissometria
La composizione di una simmetria assiale con una traslazione di vettore parallelo all'asse di simmetria è detta glissometria.
E così via.
