Cardioide

Una cardioide è una curva piana appartenente alla famiglia delle curve algebriche. Il nome deriva dal suo aspetto, che ricorda una forma di cuore.

Può essere definita geometricamente, analiticamente o in coordinate polari.

L'equazione della cardioide in coordinate polari è data da: $$ r = a (1 + \cos\theta) $$

Dove \( r \) è la distanza del punto dall'origine, \( \theta \) è l'angolo rispetto all'asse delle ascisse, \( a \) è un parametro legato al raggio del cerchio generatore.

Nota. Dal punto di vista geometrico la cardioide è il luogo dei punti tracciati dalla rotazione di un cerchio di raggio \( r \), mentre un altro cerchio di raggio uguale rotola attorno a esso, senza slittare.

Come costruire una cardioide

Per costruire geometricamente la cardioide utilizzerò Geogebra passo dopo passo.

Definisco un cerchio con centro nel punto C alle coordinate (1;1) e raggio unitario OC, dove O(0;0) è l'origine degli assi.

 

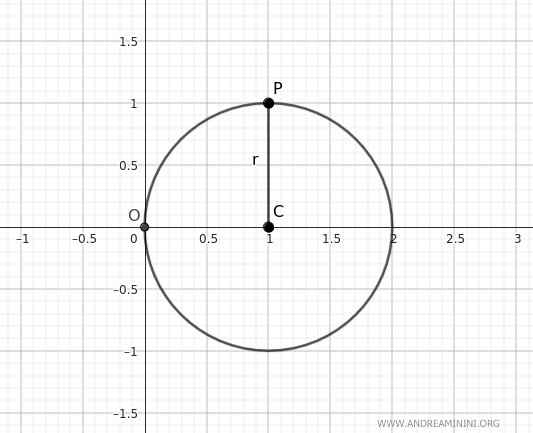
Definisco un punto mobile P lungo la circonferenza.

Poi costruisco una retta tangente alla circonferenza nel punto P.

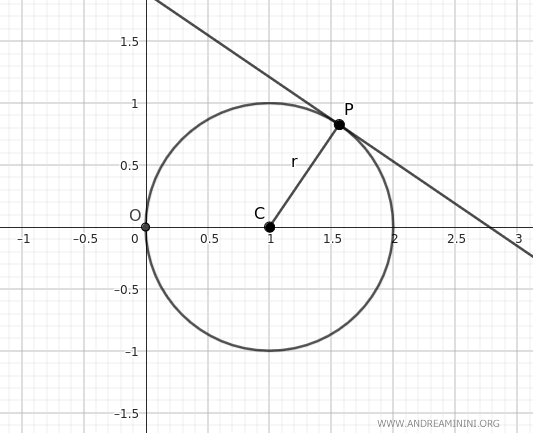
Traccio una retta parallela al segmento CP (raggio della circonferenza) che passa per l'origine degli assi (O).

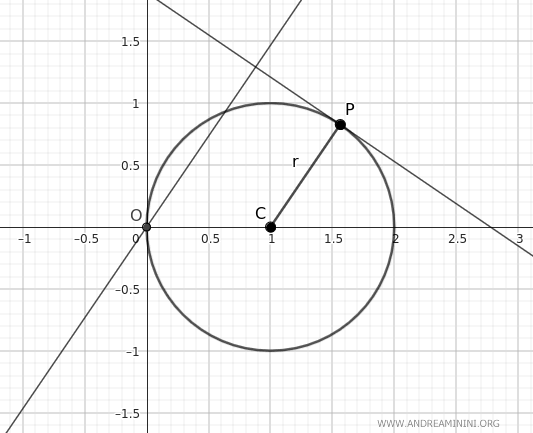
Aggiungo un punto di intersezione A tra la retta parallela al raggio e la retta tangente al punto P.

Facendo ruotare il raggio CP, il punto di intersezione A disegna la cardioide.

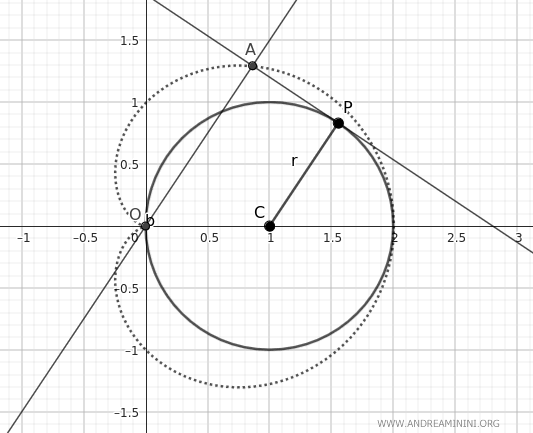
Ecco come appare l'effetto grafico della rotazione.

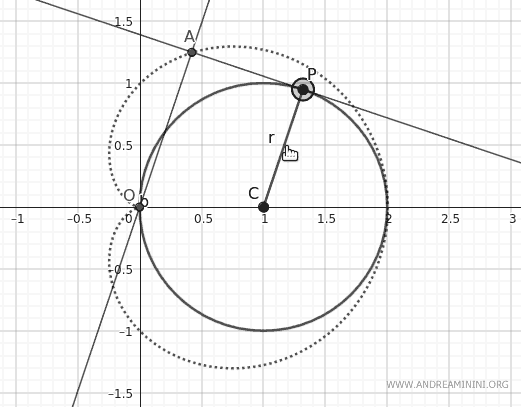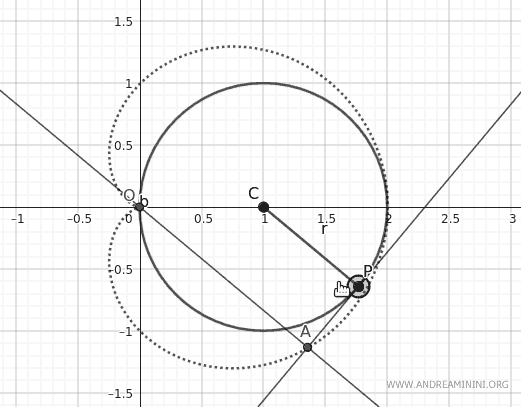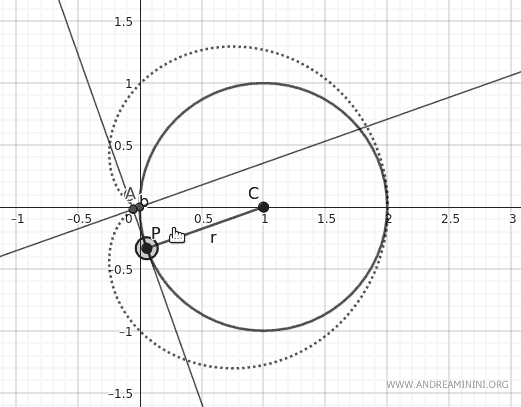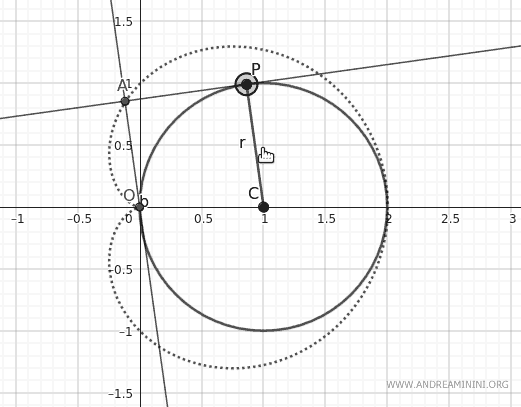
Guardando l'animazione diventa più semplice spiegare le proprietà della cardioide.

La cardioide si può definire come il luogo geometrico composto dai piedi (punti P) delle perpendicolari condotte dal punto O alle rette tangenti alla circonferenza.

In alternativa, per costruire la cardioide usando le funzioni trigonometriche, posso utilizzare il comando

Curva((-1+cos(t)) cos(t),(1-cos(t)) sin(t),t,0,2 π)

La dimostrazione

Devo dimostrare la formula della cardioide.

$$ r = a (1 + \cos\theta) $$

Nella costruzione della cardioide si possono notare due triangoli OAD e CPD.

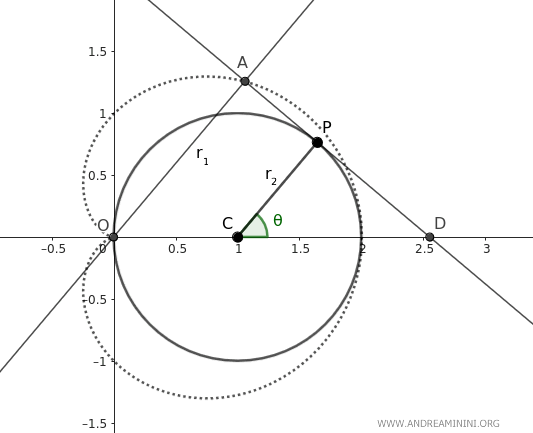
I triangoli OAD e CPD sono triangoli simili perché hanno tutti gli angoli uguali.

Quindi, i loro lati sono in proporzione tra loro.

$$ \overline{OA} :  \overline{CP} = \overline{OD} : \overline{CD} $$

Chiamo $ r_1 = \overline{OA} $ e $ r_2 = \overline{CP} $

$$ r_1 : r_2 = \overline{OD} : \overline{CD} $$

Il segmento $ \overline{OD} $ posso suddividerlo in due segmenti $ \overline{OD} = \overline{OC} + \overline{CD} $

$$ r_1 : r_2 = \overline{OC} + \overline{CD} : \overline{CD} $$

Nel triangolo CPD il segmento $ \overline{CD} $ posso scriverlo come $ \overline{CD} = \frac{ r_2 }{ \cos \theta } $ applicando il primo teorema del triangolo.

$$ r_1 : r_2 = \overline{OC} + \frac{ r_2 }{ \cos \theta } : \frac{ r_2 }{ \cos \theta } $$

Infine, il segmento $ \overline{OC} = r_2 $ è sempre il raggio della circonferenza.

$$ r_1 : r_2 = r_2 + \frac{ r_2 }{ \cos \theta } : \frac{ r_2 }{ \cos \theta } $$

Semplifico la proporzione algebricamente.

$$ \frac{r_1}{r_2}  = \frac{ r_2 + \frac{ r_2 }{ \cos \theta }}{ \frac{ r_2 }{ \cos \theta } } $$

$$ \frac{r_1}{r_2}  = ( r_2 + \frac{ r_2 }{ \cos \theta } ) \cdot \frac{ \cos \theta }{ r_2 }  $$

$$ \require{cancel} r_1  = \cancel{r_2} \cdot ( r_2 + \frac{ r_2 }{ \cos \theta } ) \cdot \frac{ \cos \theta }{ \cancel{r_2} }  $$

$$  r_1  =  ( r_2 + \frac{ r_2 }{ \cos \theta } ) \cdot  \cos \theta  $$

$$  r_1  =  \frac{ r_2  \cos \theta + r_2 }{ \cos \theta }  \cdot  \cos \theta  $$

$$  r_1  =   \frac{ r_2  \cos \theta + r_2 }{ \cancel{ \cos \theta } }  \cdot  \cancel{ \cos \theta }  $$

$$  r_1  =  r_2  \cos \theta + r_2  $$

$$  r_1  =  r_2 \cdot (1+ \cos \theta ) $$

E così via.