Distanza tra due punti in coordinate polari
La distanza tra due punti in coordinate polari \((r_1, \theta_1)\) e \((r_2, \theta_2)\) può essere calcolata utilizzando la formula derivata dalla distanza euclidea, convertendo le coordinate polari in cartesiane o direttamente in forma polare: $$ d = \sqrt{r_1^2 + r_2^2 - 2 r_1 r_2 \cos(\theta_2 - \theta_1)} $$ Dove \(r_1, r_2\) sono i moduli (distanze dall'origine) dei due punti, \(\theta_1, \theta_2\) sono gli angoli in radianti rispetto all'asse \(x\).
Il coseno \(\cos(\theta_2 - \theta_1)\) tiene conto dell'orientamento angolare dei due punti, perché determina quanto i due punti sono "allineati" rispetto all'origine:
Considerando $ \Delta \theta = \theta_2 - \theta_1 $
- Se $ \boldsymbol{ \Delta \theta = 0 } $
In questo caso \( \theta_1 = \theta_2\) e il coseno è \(\cos(\Delta \theta) = 1\) perché i due punti sono perfettamente allineati lungo la stessa direzione e verso. Quindi, la distanza è la differenza dei raggi: \(d = |r_1 - r_2|\).
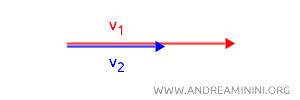
- Se $ \boldsymbol{ \Delta \theta = \pi } $
Quando la differenza è un angolo piatto (\( \theta_2 - \theta_1 = 180^\circ\)) il valore del coseno diventa \(\cos(\Delta \theta) = -1\) perché i due punti sono sulla stessa direzione ma in verso opposto. Quindi, la distanza si ottiene tramite la somma dei raggi: \(d = r_1 + r_2\).
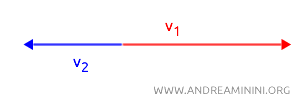
- Se $ \boldsymbol{ \Delta \theta = \frac{\pi}{2} \ o \ \Delta \theta = -\frac{\pi}{2} } $
Quando la differenza è (\(90^\circ\) o \(270^\circ\)) il coseno si annulla \(\cos(\Delta \theta) = 0\) perché i vettori sono perpendicolari. In questo caso la distanza dipende solo dalla somma dei quadrati dei raggi: \(d = \sqrt{r_1^2 + r_2^2}\).
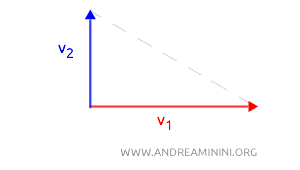
Nota. Questa formula è particolarmente utile in contesti geometrici e applicazioni come la robotica o la grafica computerizzata, dove le coordinate polari sono comuni.
Un esempio pratico
Considero due punti con coordinate polari
$$ P_1( r_1 ; \theta_1 ) = (5 ; \frac{\pi}{4}) $$
$$ P_2( r_2 ; \theta_2 ) = ( 7 ; \frac{\pi}{3}) $$
Quindi, i moduli sono $ r_1 = 5 $ e $ r_2 = 7 $ mentre gli argomenti sono $ \theta_1 = \frac{\pi}{4} $ e $ \theta_2 = \frac{\pi}{3} $ ossia $ \theta_1 = 45° $ e $ \theta_2 = 60° $.
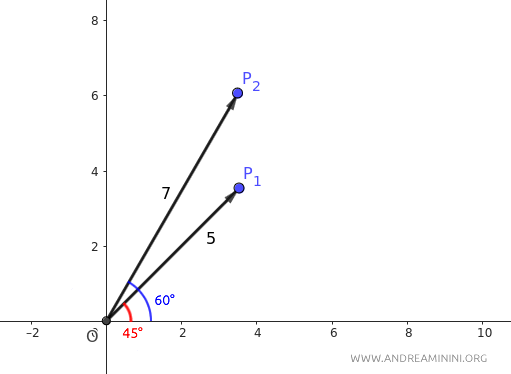
Calcolo la distanza tra i punti usando la formula:
$$ d = \sqrt{r_1^2 + r_2^2 - 2r_1r_2\cos(\theta_2 - \theta_1)} $$
Per prima cosa determino la differenza tra gli angoli \(\theta_2 - \theta_1\):
$$ \theta_2 - \theta_1 = \frac{\pi}{3} - \frac{\pi}{4} = \frac{4\pi}{12} - \frac{3\pi}{12} = \frac{\pi}{12} $$
Poi calcolo il coseno \(\cos(\theta_2 - \theta_1)\):
$$ \cos\left(\frac{\pi}{12}\right) \approx 0.9659 \quad \text{(approssimato)} $$
Sostituisco il risultato del coseno nella formula e svolgo i calcoli.
$$ d = \sqrt{5^2 + 7^2 - 2 \cdot 5 \cdot 7 \cdot \cos\left(\frac{\pi}{12}\right)} $$
$$ d = \sqrt{25 + 49 - 70 \cdot 0.9659} $$
$$ d = \sqrt{25 + 49 - 67.613} $$
$$ d = \sqrt{74 - 67.613} $$
$$ d = \sqrt{6.387} $$
$$ d \approx 2.53 $$
La distanza tra i due punti è approssimativamente \( d \approx 2.53 \).
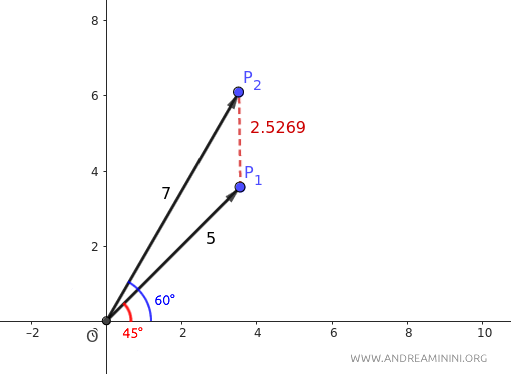
Verifica. Per verificare il calcolo della distanza trasformo le coordinate polari \((r, \theta)\) dei due punti in coordinate cartesiane \((x, y)\) usando le formule.
$$ x = r \cos(\theta), \quad y = r \sin(\theta) $$
Le coordinate cartesiane del punto \(P_1\) sono $ P_1 \approx (3.54, 3.54) $
$$ x_1 = 5 \cos\left(\frac{\pi}{4}\right), \quad y_1 = 5 \sin\left(\frac{\pi}{4}\right) $$
$$ x_1 = 5 \cdot 0.7071 \approx 3.5355, \quad y_1 = 5 \cdot 0.7071 \approx 3.5355 $$
Le coordinate cartesiane del punto \(P_1\) sono $ P_2 \approx (3.5, 6.06) $
$$ x_2 = 7 \cos\left(\frac{\pi}{3}\right), \quad y_2 = 7 \sin\left(\frac{\pi}{3}\right) $$
$$ x_2 = 7 \cdot 0.5 = 3.5, \quad y_2 = 7 \cdot 0.866 \approx 6.062 $$
La distanza tra due punti in coordinate cartesiane \((x_1, y_1)\) e \((x_2, y_2)\) è data dalla formula:
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
$$ d = \sqrt{(3.5 - 3.54)^2 + (6.06 - 3.54)^2} $$
$$ d = \sqrt{(-0.04)^2 + (2.52)^2} $$
$$ d = \sqrt{0.0016 + 6.3504} $$
$$ d = \sqrt{6.352} $$
$$ d \approx 2.53 $$
La distanza calcolata con le coordinate cartesiane è \(d \approx 2.53\), come quella già ottenuta con il calcolo in coordinate polari.
Dimostrazione
La formula si ottiene applicando la legge del coseno di un triangolo formato dall'origine e dai due punti:
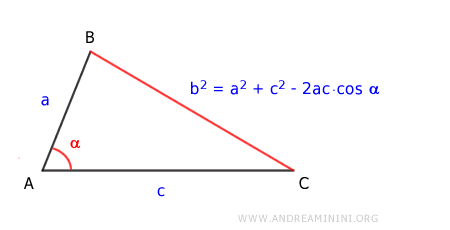
Se assumo il vertice \( A \) come origine del sistema di assi e considero i punti \( B \) e \( C \) come quelli tra cui desidero calcolare la distanza, posso utilizzare la legge del coseno applicata al triangolo \( ABC \) per determinare direttamente la distanza tra i due punti, senza dover trasformare le coordinate in cartesiane.
E così via.
