Equazione della retta in coordinate polari
L'equazione della retta passante per l'origine
In coordinate polari, l'equazione di una retta passante per l'origine si esprime tramite l'angolo \( \alpha \) (in radianti o gradi), che rappresenta l'inclinazione della retta rispetto al semiasse positivo delle ascisse (l'asse \(x\)).
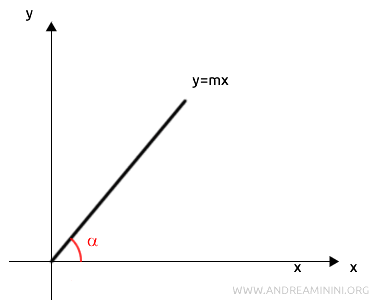
Per dimostrare che una retta passante per l'origine in coordinate polari è definita unicamente dall'angolo \( \alpha \), posso partire dall'equazione della retta in coordinate cartesiane:
$$ y = mx $$
dove \( m \) è il coefficiente angolare della retta.
Prendo un punto \( P \) appartenente alla retta, con coordinate cartesiane \( (x, y) \).
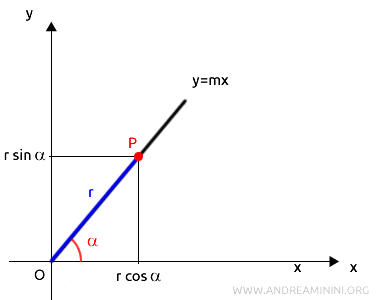
In coordinate polari, queste coordinate si possono esprimere come:
$$ x = r \cos \alpha, \quad y = r \sin \alpha $$
Dove:
- \( \alpha \) è l'angolo tra l'asse polare (asse x) e la direzione della retta,
- \( r \) è la distanza del punto \( P \) dall'origine (modulo del vettore posizione).
Sostituendo queste espressioni nell'equazione \( y = mx \), ottengo:
$$ r \sin \alpha = m (r \cos \alpha) $$
Semplifico entrambi i membri dividendo per \( r \) (assumendo \( r \neq 0 \)):
$$ \sin \alpha = m \cos \alpha $$
Il coefficiente angolare \( m \) della retta è quindi dato da:
$$ m = \frac{\sin \alpha}{\cos \alpha} = \tan \alpha $$
Con $ \alpha \ne \frac{\pi}{2} + k \pi $ per evitare che l'angolo α sia un angolo retto.
Questo dimostra che la retta è completamente definita dall'angolo \( \alpha \), che rappresenta l'inclinazione della retta rispetto al semiasse positivo delle ascisse.
Pertanto, in coordinate polari, una retta passante per l'origine è rappresentata unicamente dall'angolo \( \alpha \).
Un esempio pratico
Voglio descrivere la retta passante per l'origine che forma un angolo di \( \alpha = \frac{\pi}{4} \) (45 gradi) con il semiasse positivo delle ascisse.
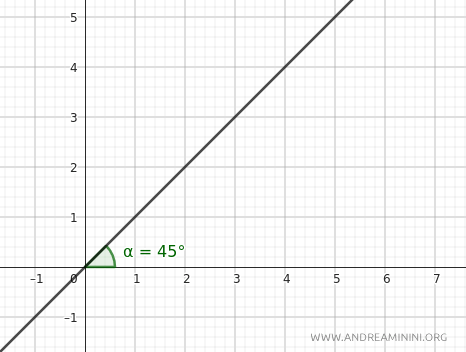
In coordinate cartesiane, una retta che passa per l'origine e ha un angolo \( \alpha \) rispetto all'asse \( x \) ha il coefficiente angolare:
$$ m = \tan \alpha $$
Per \( \alpha = \frac{\pi}{4} \), il coefficiente angolare è:
$$ m = \tan \frac{\pi}{4} = 1 $$
Quindi, l'equazione cartesiana della retta è:
$$ y = x $$
Le coordinate polari di un generico punto \( P \) sulla retta sono:
$$ x = r \cos \alpha, \quad y = r \sin \alpha $$
Sostituisco \( \alpha = \frac{\pi}{4} \):
$$ x = r \cos \frac{\pi}{4} = \frac{r}{\sqrt{2}}, \quad y = r \sin \frac{\pi}{4} = \frac{r}{\sqrt{2}} $$
Quindi, le coordinate cartesiane di un punto \( P \) della retta sono:
$$ (x, y) = \left(\frac{r}{\sqrt{2}}, \frac{r}{\sqrt{2}}\right) $$
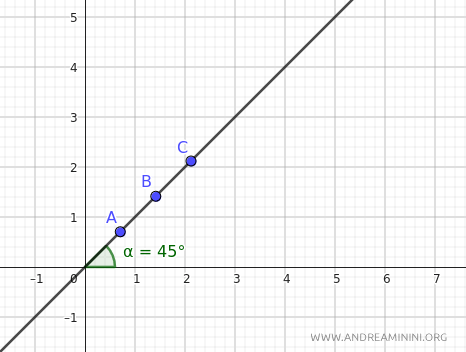
Qualunque punto \( P \) appartenente alla retta soddisfa questa relazione, con \( r \) che varia liberamente per descrivere l'intera retta.
- Per \( r = 1 \), \( P_A = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \)
- Per \( r = 2 \), \( P_B = (\frac{2}{\sqrt{2}}, \frac{2}{\sqrt{2}}) \)
- Per \( r = 1 \), \( P_C = (\frac{3}{\sqrt{2}}, \frac{3}{\sqrt{2}}) \)
L'equazione di una retta non passante per l'origine
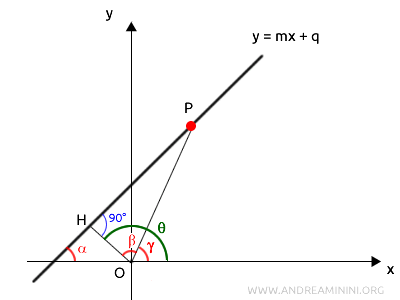
L'equazione di una retta non passante per l'origine in forma polare è la seguente $$ d = r \cos (\theta - \gamma) $$ Dove \( d \) è la distanza della retta dal polo (origine \( O \)) mentre \( \theta \) è l'angolo tra l'asse polare e il segmento \( \overline{OH} \) della distanza.
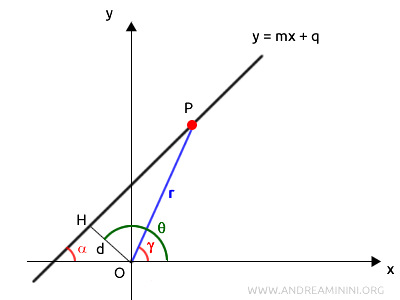
Ogni punto della retta è una coppia di valori $ P[ r; \gamma] $ dove $ r $ è la lunghezza del segmento \( \overline{OP} \) e $ \gamma $ è l'angolo tra l'asse polare e \( \overline{OP} \).
Per dimostrarlo considero una retta qualsiasi non passante per l'origine, che forma un angolo \( \alpha \) con l'asse polare.
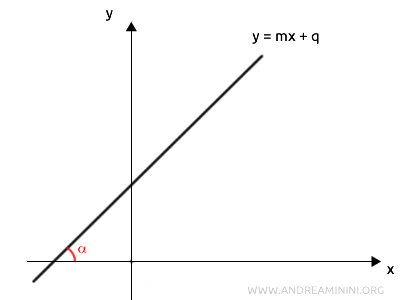
Considero un punto \( P \) arbitrario appartenente alla retta e il segmento \( \overline{OP} \), che congiunge il polo \( O \) con \( P \).
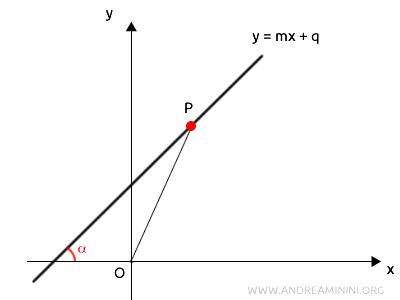
Poi traccio la distanza la distanza \( \overline{OH} \), perpendicolare alla retta.
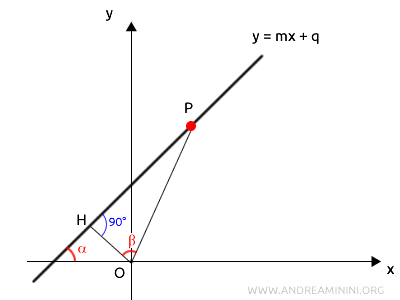
I punti $ OHP $ formano un triangolo rettangolo.
Secondo il primo teorema del triangolo rettangolo, un cateto \( \overline{OH} \) è uguale all'ipotenusa \( \overline{OP} \) per il coseno dell'angolo acuto \( \beta \) adiacente al cateto \( \overline{OH} \).
$$ \overline{OH} = \overline{OP} \cdot \cos \beta $$
Il segmento \(\overline{OH}=d \) è la distanza, mentre il segmento \( \overline{OP}=r ) è il raggio che collega il punto $ P $ con l'origine (polo).
$$ d = r \cdot \cos \beta $$
Noto che l'angolo \( \beta \) può essere espresso come differenza tra gli angoli \( \theta \) (angolo polare del punto \( P \)) e \( \gamma \):
Sostituendo \( \beta \) nell'equazione precedente, posso concludere che la distanza della retta dall'origine è:
$$ d = r \cdot \cos ( \theta - \gamma ) $$
Un esempio pratico
Considero l'equazione di una retta in forma cartesiana ossia $ y =mx + q $
$$ y = \sqrt{3}x + 2 $$
Il coefficiente angolare \( m = \sqrt{3} \) mi permette di calcolare \( \alpha \) usando la relazione:
$$ m = \tan \alpha \implies \alpha = \arctan(\sqrt{3}) $$
Sapendo che \( \tan \alpha = \sqrt{3} \), ottengo:
$$ \alpha = \frac{\pi}{3} $$
Una volta noto l'angolo $ \alpha $, calcolo l'angolo $ \theta $ tra l'asse polare e il segmento perpendicolare alla retta che misura la distanza.
Il coefficiente angolare di un segmento perpendicolare a una retta $ y =mx + q $ è $ m_{normale}=- \frac{1}{m} $
$$ m_{normale}=- \frac{1}{m} = -\frac{1}{ \sqrt{3}} $$
Quindi, sapendo che $ \tan \theta = -\frac{1}{ \sqrt{3}} $, l'angolo $ \theta $ lo ottengo calcolando l'arcotangente
$$ \theta = \arctan ( -\frac{1}{ \sqrt{3}} ) = - \frac{\pi}{6} $$
Poiché l'angolo si trova nel II quadrante, devo considerare l'angolo equivalente:
$$ \theta = - \frac{\pi}{6} = \pi - \frac{\pi}{6} = \frac{6 \pi - \pi}{6} = \frac{5 \pi}{6} $$
La distanza della retta dall'origine \( d \) è data dalla formula generale per la distanza punto-retta:
$$ d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}} $$
Dove l'equazione della retta è riscritta nella forma generale:
$$ Ax + By + C = 0 $$
Dove $ A = -\sqrt{3}, \quad B = -1, \quad C = -2 $ e il punto \( O \) ha coordinate \( (x_0, y_0) = (0, 0) \). Sostituendo, ottengo:
$$ d = \frac{|-\sqrt{3}(0) - 1(0) - 2|}{\sqrt{(-\sqrt{3})^2 + (-1)^2}} = \frac{|-2|}{\sqrt{3 + 1}} = \frac{2}{2} = 1 $$
Quindi la distanza è uguale a $ d=1 $
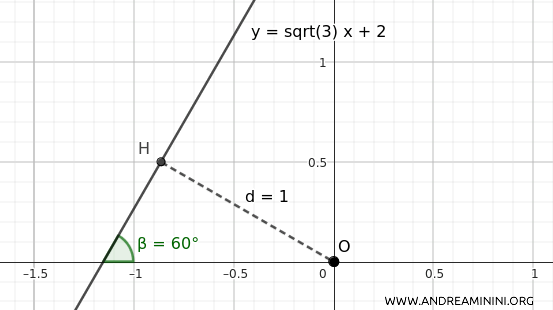
L'equazione della retta in forma polare è data da:
$$ d = r \cos(\theta - \gamma) $$
Sapendo che $ d=1 $ e $ \theta = \frac{5 \pi}{6} $
$$ 1 = r \cos ( \frac{5 \pi}{6} - \gamma) $$
Quindi, l'equazione in forma polare della retta \( y = \sqrt{3}x + 2 \) è:
$$ r \cos ( \frac{5 \pi}{6} - \gamma ) = 1 $$
Verifica. Per verificare il risultato, calcolo il procedimento inverso. Trasformo l'equazione polare in un'equazione in forma cartesiana.
$$ r \cos ( \frac{5 \pi}{6} - \gamma ) = 1 $$
Applico la formula della sottrazione del coseno.
$$ r \cos ( \frac{5 \pi}{6} ) \cos ( \gamma ) + r \sin ( \frac{5 \pi}{6} ) \sin ( \gamma ) = 1 $$
Sapendo che $ x = r \cos (\gamma ) $ e $ y = r \sin (\gamma ) $
$$ \cos ( \frac{5 \pi}{6} ) x + \sin ( \frac{5 \pi}{6} ) y = 1 $$
Calcolo il valore del seno e del coseno ossia $ \cos ( \frac{5 \pi}{6} ) = - \frac{ \sqrt{3} }{2} $ e $ \sin ( \frac{5 \pi}{6} ) = \frac{ 1 }{2} $
$$ - \frac{ \sqrt{3} }{2} x + \frac{1}{2} y = 1 $$
Moltiplico per due entrambi i lati dell'equazione per eliminare i denominatori delle frazioni.
$$ 2 \cdot \frac{ - \sqrt{3} }{2} x + \frac{1}{2} y = 1 \cdot 2 $$
$$ - \sqrt{3}x + y = 2 $$
$$ y = \sqrt{3}x + 2 $$
E così via.
