Spirale di Archimede
La spirale di Archimede è una curva piana generata da un punto che si muove con velocità costante lungo una semiretta che ruota con velocità angolare costante attorno a un punto fisso, detto polo.
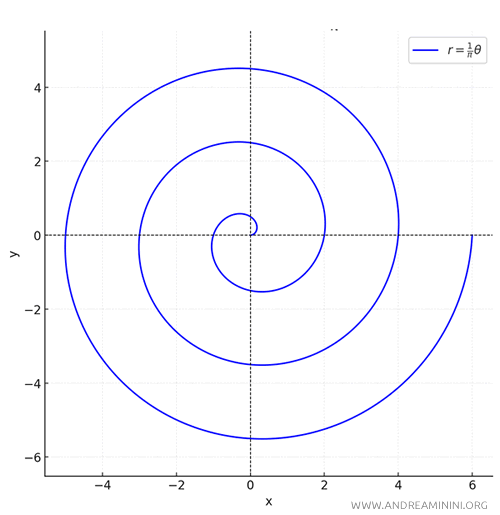
Questa curva è descritta in coordinate polari dall'equazione: $$ r = a \cdot \theta + b $$
Dove:
- \( r \) è la distanza dal centro (detto polo)
- \( \theta \) è l'angolo in radianti
- \( a \) e \( b \) sono parametri reali, con \( a \neq 0 \). Se \( a>0 \) la spirale gira in senso antiorario e viceversa.
In pratica, è una sorta di disco con una semiretta che gira attorno al polo con velocità angolare costante, con un punto sopra che si sposta piano piano verso l'esterno lungo la direzione radiale.
Nota. A differenza di altre spirali (come quella logaritmica), dove l'incremento è esponenziale, nella spirale di archimede il raggio \( r \) aumenta in modo lineare rispetto all'angolo \( \theta \), con una distanza costante. Quindi, le spire successive sono equidistanti tra loro.
Un esempio pratico
Costruisco la spirale con questi parametri
$$ a = \frac{1}{\pi} $$
$$ b = 0 $$
L'equazione della spirale diventa
$$ r = \frac{1}{\pi} \cdot \theta $$
In questo caso, la distanza \( r \) dal polo cresce linearmente con l'angolo \( \theta \), con un coefficiente di proporzionalità \( \frac{1}{\pi} \).
Quindi, la distanza \( r \) aumenta in modo proporzionale all'angolo \( \theta \). Per ogni incremento di \( \pi \) in \( \theta \), \( r \) cresce di 1.
Non c'è alcun termine costante (\( b = 0 \)), quindi la curva parte direttamente dal polo (\( r = 0 \) quando \( \theta = 0 \)).
Calcolo le coordinate polari di alcuni punti della spirale
| \( \theta \) | \( r = \frac{1}{\pi} \theta \) |
|---|---|
| 0 | 0 |
| \( \frac{\pi}{2} \) | \( \frac{1}{2} \) |
| \( \pi \) | 1 |
| \( \frac{3\pi}{2} \) | \( \frac{3}{2} \) |
| \( 2\pi \) | 2 |
| \( \frac{5\pi}{2} \) | \( \frac{5}{2} \) |
| \( 3\pi \) | 3 |
| \( \frac{7\pi}{2} \) | \( \frac{7}{2} \) |
La prima colonna (\( \theta \)) rappresenta l'angolo in radianti. La seconda colonna (\( r \)), invece, rappresenta il valore del raggio calcolato con \( r = \frac{1}{\pi} \theta \).
Riportando le coordinate di questi punti sul piano ottengo una spirale. Per farlo si può usare anche Geogebra.
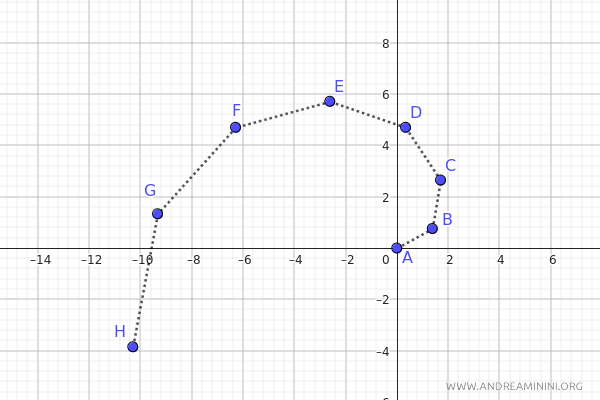
Come si può osservare, la curva si espande dal polo verso l'esterno con una crescita uniforme, tracciando spire equidistanti man mano che l'angolo \( \theta \) aumenta.
Ecco il grafico completo della spirale di Archimede con l'equazione \( r = \frac{1}{\pi} \cdot \theta \).

E così via.
