Distanza di una retta parallela al piano

La distanza $d$ di una retta $r$ parallela a un piano $\pi$ si calcola trovando un punto $P$ sulla retta e proiettando perpendicolarmente questo punto sul piano.

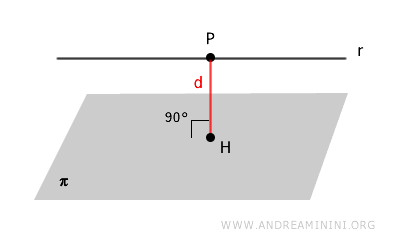
La formula per calcolare la distanza $d$ tra il punto $P(x_0, y_0, z_0)$ e il piano dato dall'equazione $ax + by + cz + d = 0$ è:

$$d = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}}$$

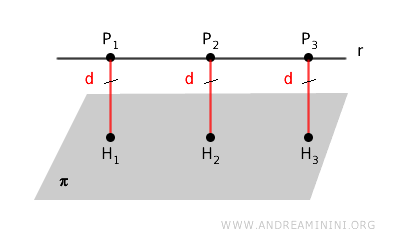
Questa mi formula fornisce la lunghezza del segmento perpendicolare che congiunge $P$ al piano $\pi$, ed è la stessa distanza per ogni punto sulla retta $r$ dato che la retta è parallela al piano.

Esempio

Considero il piano $\pi$ definito dall'equazione:

$$2x - 3y + 6z + 9 = 0$$

Supponiamo che la retta $r$ sia definita dalle equazioni parametriche:

$$x = 13+3t$$

$$y = 2t$$

$$z = 0$$

Devo prima verificare che la retta $r$ sia effettivamente parallela al piano $\pi$, calcolando il prodotto scalare tra il vettore normale del piano $(2, -3, 6)$ e la direzione della retta $(3, 2, 0)$:

$$2 \cdot 3 + (-3) \cdot 2 + 6 \cdot 0 = 6 - 6 + 0 = 0$$

Il prodotto scalare è zero, quindi la retta è parallela al piano.

Scelgo un punto sulla retta $r$, ad esempio, quando $t = 0$, il punto è $(13, 0, 0)$. Applichiamo la formula per la distanza:

$$d = \frac{|2(13) - 3(0) + 6(0) + 9|}{\sqrt{2^2 + (-3)^2 + 6^2}}$$

$$d = \frac{|26 + 9|}{\sqrt{4 + 9 + 36}}$$

$$d = \frac{|35|}{\sqrt{49}}$$

$$d = \frac{35}{7} = 5$$

Quindi, la distanza della retta $r$ dal piano $\pi$ è 5.

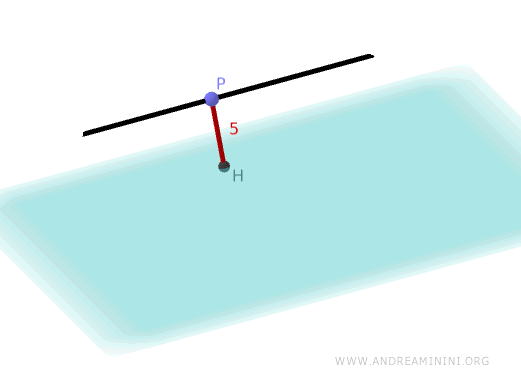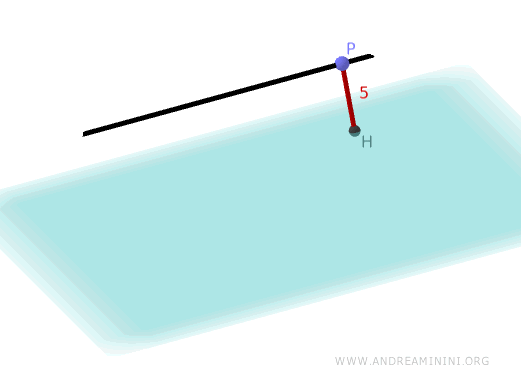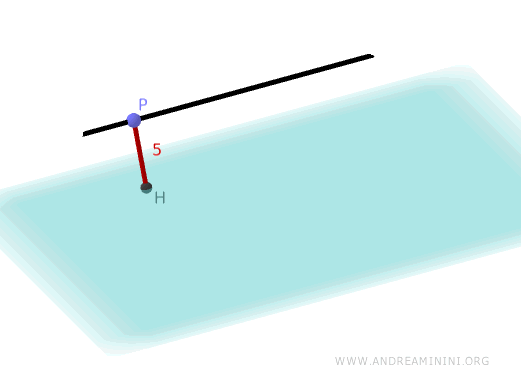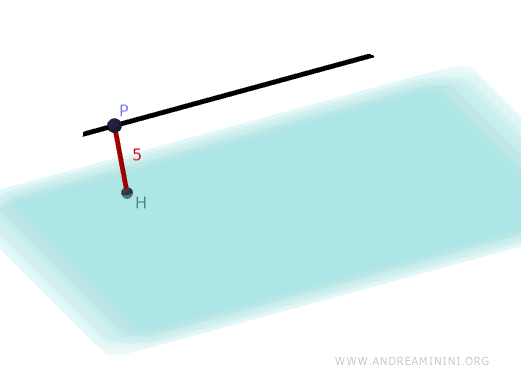
E così via.