Formula di sdoppiamento di una conica

La formula di sdoppiamento (o regola di sdoppiamento) è un metodo della geometria analitica che permette di determinare l'equazione della retta tangente a una conica in un piano cartesiano nel punto \( P(x_0, y_0) \). $$  a_{11}x_0 x + a_{22}y_0 y + a_{12}(x y_0 + x_0 y) + \\ + a_{01}(x + x_0) + a_{02}(y + y_0) + a_{00} = 0 $$ I coefficienti sono tratti dall'equazione della conica:
$ a_{11}x^2 + a_{22}y^2 + 2a_{12}xy + 2a_{01}x + 2a_{02}y + a_{00} = 0 $

In altre parole la formula di sdoppiamento mi permette di trovare l'equazione della tangente trasformando opportunamente i termini dell'equazione originale della conica senza l'uso delle derivate.

Una conica è descritta dall'equazione generale:

$$ a_{11}x^2 + a_{22}y^2 + 2a_{12}xy + 2a_{01}x + 2a_{02}y + a_{00} = 0 $$

La regola dello sdoppiamento stabilisce che l'equazione della retta tangente in \( P(x_0, y_0) \) si ottiene effettuando le seguenti sostituzioni formali nelle variabili dell'equazione della conica:

Sostituzioni per i termini di secondo grado:

• \( x^2 \rightarrow x_0 x \)
• \( y^2 \rightarrow y_0 y \)
• \( xy \rightarrow \frac{1}{2}(x y_0 + x_0 y) \)

Sostituzioni per i termini di primo grado:

• \( x \rightarrow \frac{1}{2}(x + x_0) \)
• \( y \rightarrow \frac{1}{2}(y + y_0) \)

Applicando queste sostituzioni all'equazione della conica, si ottiene l'equazione della retta tangente alla conica nel punto \( P(x_0, y_0) \):

$$  a_{11}x_0 x + a_{22}y_0 y + a_{12}(x y_0 + x_0 y) + a_{01}(x + x_0) + a_{02}(y + y_0) + a_{00} = 0 $$

Nota. Ricordarsi la formula di sdoppiamento di una conica può essere molto difficile. Un metodo per ricordarla è attuare le sostituzioni formali direttamente all'equazione della conica. Inizia dall'equazione della conica che già conosci e sostituisci i termini quadratici con $$ x^2 \rightarrow x_0 x $$ $$ y^2 \rightarrow y_0 y $$ Poi sostituisci xy con la loro media $$ xy \rightarrow \frac{1}{2}(x y_0 + x_0 y) $$ Infine, sostituisci i termini lineari x e y con le seguenti medie $$ x \rightarrow \frac{1}{2}(x + x_0) $$ $$ y \rightarrow \frac{1}{2}(y + y_0) $$ Dove x₀ e y₀ sono le coordinate del punto di tangenza.  Questo escamotage mnemonico aiuta a ricordare la formula di sdoppiamento in modo più semplice.

Un esempio pratico

Faccio un esempio pratico usando la formula di sdoppiamento per trovare l'equazione della retta tangente a una conica.

Considero un'ellisse data dall'equazione:

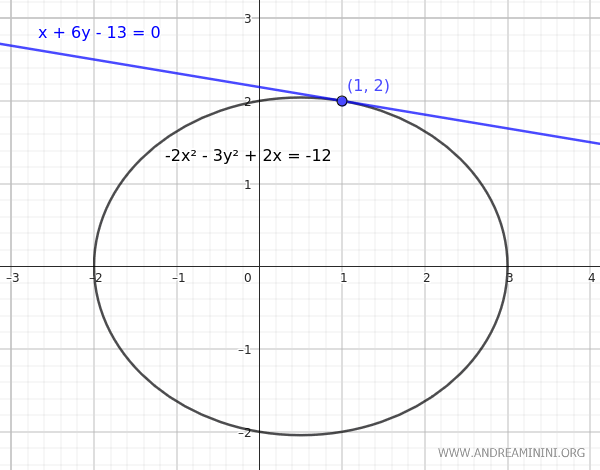
$$ -2x^2 - 3y^2 + 2x = -12 $$

La scrivo in forma generale

$$ -2x^2 - 3y^2 + 2x + 12 = 0 $$

Voglio trovare l'equazione della retta tangente a questa ellisse nel punto \( P(1, 2) \).

$$ -2x^2 - 3y^2 + 2x + 12 = 0 $$

Applico le sostituzioni formali ai termini dell'equazione della conica.

Le sostituzioni per i termini di secondo grado sono:

$$ x^2 \rightarrow x_0 x $$

$$ y^2 \rightarrow y_0 y  $$

Quindi, l'equazione della conica diventa

$$ -2x_0 x - 3y_0 y + 2x + 12 = 0 $$

Sostituisco il termine lineare \( x \rightarrow \frac{1}{2}(x + x_0) \)

$$ -2x_0 x - 3y_0 y + 2 \cdot \frac{1}{2}(x+x_0) + 12 = 0 $$

$$ -2x_0 x - 3y_0 y + (x+x_0) + 12 = 0 $$

$$ -2x_0 x - 3y_0 y + x +x_0 + 12 = 0 $$

Il punto di tangenza che voglio trovare si trova alle coordinate P(1,2) ovvero $ x_0 = 1 $ e $ y_0=2 $

$$ -2 \cdot 1 \cdot x - 3 \cdot 2 \cdot y + x + 1 + 12 = 0 $$

$$ -x -6y  + 13 = 0 $$

Semplifico ulteriormente moltiplicando entrambi i membri dell'equazione per -1

$$ x + 6y  - 13 = 0 $$

Il risultato finale è l'equazione della retta tangente nel punto P(1,2).

Soluzione alternativa

Per trovare la retta tangente alla conica nel punto P(1,2) posso anche seguire quest'altra procedura.

$$ -2x^2 - 3y^2 + 2x + 12 = 0 $$

Sapendo che in generale l'equazione di una conica è la seguente:

$ a_{11}x^2 + a_{22}y^2 + 2a_{12}xy + 2a_{01}x + 2a_{02}y + a_{00} = 0 $

Identifico i coefficienti della conica $ 4x^2 + 9y^2 - 36 = 0  $ che in questo caso sono:

•  \( a_{11} = -2 \)
•  \( a_{22} = -3 \)
•  \( a_{12} = 0 \) (poiché non c'è termine \( xy \))
•  \( a_{01} = 1 \) (poiché $ 2a_{01}x = 2 $ quindi $ a_{01}=\frac{1}{2} \cdot 2 = 1 $)
•  \( a_{02} = 0 \) (poiché non c'è termine \( y \))
•  \( a_{00} = -12 \)

A questo punto scrivo la formula di sdoppiamento della conica.

$$  a_{11}x_0 x + a_{22}y_0 y + a_{12}(x y_0 + x_0 y) + a_{01}(x + x_0) + a_{02}(y + y_0) + a_{00} = 0 $$

Sostituisco i coefficienti che ho appena trovato.

$$  -2x_0 x -3y_0 y + 0 \cdot (x y_0 + x_0 y) + 1 \cdot (x + x_0) + 0 \cdot (y + y_0) +12 = 0 $$

$$  -2x_0 x - 3y_0 y +x + x_0  +12 = 0 $$

In questo caso il punto di tangenza si trova alle coordinate \( P(1, 2) \), quindi $ x_0=1 $ e $ y_0 = 2 $

$$ -2 \cdot 1 \cdot x - 3 \cdot 2 \cdot y + x + 1 +12 = 0 $$

$$ -x - 6y +13 = 0 $$

$$ x+6y - 13=0 $$  

Questa è l'equazione della retta tangente cercata. 

Ho così trovato l'equazione tangente alla conica nel punto P(1,2).

E così via.