Piani perpendicolari

Due piani incidenti sono detti piani perpendicolari quando formano un diedro retto (90°).

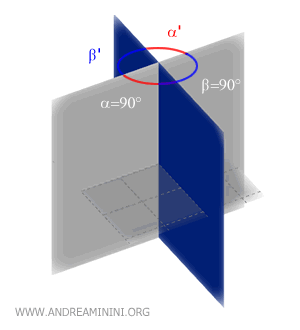
In altre parole, l'angolo tra i due piani perpendicolari è un angolo di 90° (angolo retto).

Quindi, due piani perpendicolari dividono lo spazio in quattro diedri retti.

Sono anche detti piani normali o piani ortogonali.

I piani perpendicolari si distinguono dai piani obliqui. I piani sono detti obliqui quando sono incidenti ma non formano un diedro retto, ossia quando hanno un angolo diedrale diverso da 90°.

Quando due piani formano un diedro retto, di fatto ne formano anche altri tre diedri retti, perché i diedri opposti sono congruenti.

Quindi, si può dire anche che due piani perpendicolari dividono lo spazio tridimensionale in quattro diedri retti, ossia quattro diedri con un angolo diedrale di 90°.

Condizioni di perpendicolarità tra piani

Vediamo come riconoscere quando due piani sono perpendicolari.

Come nel caso delle rette, anche per i piani la perpendicolarità si basa sull’orientamento reciproco: due piani sono perpendicolari se l’angolo formato tra di essi è retto (90°).

Dati due piani con equazioni generali: $$\pi_1: \ a x + b y + c z + d = 0 $$ $$ \pi_2: \ a' x + b' y + c' z + d' = 0 $$ I due piani sono perpendicolari se e solo se il prodotto scalare dei rispettivi vettori normali è nullo, cioè: $$a \cdot a' + b \cdot b' + c \cdot c' = 0 $$

Ogni piano è caratterizzato da un vettore normale, che è perpendicolare al piano stesso:

$$ \vec{n_1} = (a, b, c) $$

$$ \vec{n_2} = (a', b', c') $$

L’angolo tra due piani corrisponde all’angolo tra i loro vettori normali.

Quindi, se il prodotto scalare dei normali è nullo, allora i vettori sono ortogonali, e di conseguenza anche i piani sono perpendicolari.

Esempio

Considero due piani con le seguenti equazioni generali:

$$ \pi_1: \ 2x + 3y + z - 5 = 0 $$

$$ \pi_2: \ 4x - 6y - 2z + 1 = 0 $$

Calcolo il prodotto scalare dei vettori normali:

$$a \cdot a' + b \cdot b' + c \cdot c' $$

$$ (2, 3, 1) \cdot (4, -6, -2) = 2 \cdot 4 + 3 \cdot (-6) + 1 \cdot (-2) = 8 - 18 - 2 = -12 $$

Poiché il prodotto scalare è diverso da zero, i due piani non sono perpendicolari.

Caso di equazioni in forma esplicita

Quando le equazioni dei due piani sono scritte in forma esplicita: $$ \pi_1: \ z = m x + n y + q $$ $$ \pi_2: \ z = m' x + n' y + q' $$ la condizione di perpendicolarità tra i due piani diventa: $$ m \cdot m' + n \cdot n' = -1 $$

Questa formula è analoga a quella per la perpendicolarità tra rette nel piano \$ xy \$.

In questo caso, i coefficienti $ m $ e $ n $ rappresentano le "pendenze" del piano rispetto agli assi $ x $ e $ y $.

Esempio

Considero i due piani con le seguenti equazioni in forma esplicita:

$$ \pi_1: \ z = 2x + 3y + 1 $$

$$ \pi_2: \ z = -\frac{1}{2}x - \frac{1}{3}y + 4 $$

Voglio verificare se questi due piani sono perpendicolari.

Quando i piani sono scritti in forma esplicita $ z = m x + n y + q $ la condizione di perpendicolarità è:

$$ m \cdot m' + n \cdot n' = -1 $$

In questo caso nel primo piano $ m= 2 $ e $ n = 3 $ mentre nel secondo piano $ m' = -\frac{1}{2} $ e $ n' = -\frac{1}{3} $.

$$ m \cdot m' + n \cdot n' = 2 \cdot \left( -\frac{1}{2} \right) + 3 \cdot \left( -\frac{1}{3} \right)  = -1 + (-1) = -2 $$

Il prodotto scalare è diverso da -1

$$ m \cdot m' + n \cdot n' = -2 \neq -1 $$

Quindi, i ipiani non sono perpendicolari.

Se invece avessi trovato: $$ m \cdot m' + n \cdot n' = -1 $$ allora i piani sarebbero stati perpendicolari.

E così via.