Iperboloide

Un iperboloide è una superficie quadrica nello spazio a tre dimensioni che può avere due forme principali: l'iperboloide a una falda e l'iperboloide a due falde. Queste superfici sono definite da equazioni diverse.

• Iperboloide a una falda
  Un iperboloide a una falda è una superficie che si estende all'infinito in tutte le direzioni e ha una forma che può essere visualizzata come un "collo di bottiglia" o una sella. E' anche detto "iperbolide iperbolico". L'equazione generale è una polinomiale di secondo grado: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1 $$ Dove \(a\), \(b\) e \(c\) sono parametri che determinano le dimensioni dell'iperboloide lungo gli assi \(x\), \(y\) e \(z\). Le sezioni orizzontali (piani \(z = \text{costante}\)) sono ellissi mentre le sezioni verticali (piani paralleli agli assi \(x\) o \(y\)) sono iperboli. Questa superficie è continua e connessa.
  
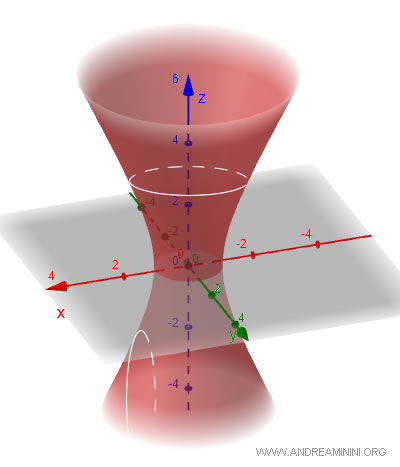
• Iperboloide a due falde
  Un iperboloide a due falde è una superficie che consiste di due parti separate e opposte (due falde) che si allontanano simmetricamente dal centro. E' anche detto "iperbolide ellittico". L'equazione generale è: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = -1 $$ Anche qui, \(a\), \(b\), e \(c\) sono parametri che determinano le dimensioni dell'iperboloide. Le sezioni orizzontali (piani \(z = \text{costante}\)) sono ancora ellissi. Le sezioni verticali sono iperboli, ma a differenza dell'iperboloide a una falda, le due parti della superficie sono separate tra loro. Quindi, non è una superficie continua, né connessa.
  

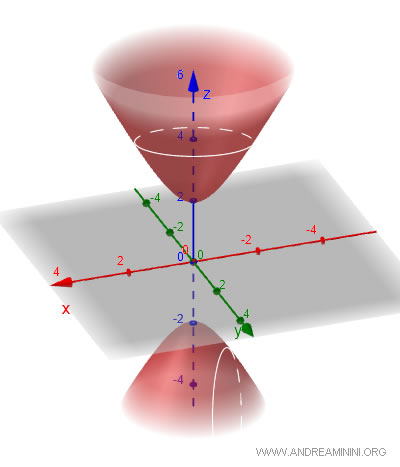
Gli iperboloidi sono superfici rigate, il che significa che possono essere generate da linee rette. Questo li rende strutturalmente interessanti.

Spesso sono usati in architettura e ingegneria per creare strutture leggere ma robuste, come torri, cupole o strutture reticolari.

E così via.