Paraboloide

Un parabolide è una superficie quadrica nello spazio a tre dimensioni che deriva dalla parabola. 

Esistono due forme principali di parabolide a seconda del processo seguito per crearla: la rotazione o la traslazione di una parabola. 

• Parabolide ellittico
  Questa superficie si forma ruotando una parabola attorno al suo asse simmetrico, generalmente verticale. Il risultato è una struttura a forma di coppa o di piatto profondo. Le sezioni orizzontali sono ellissi, mentre le sezioni verticali sono parabole. L'equazione generale di un parabolide ellittico è: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = \frac{z}{c} $$ Dove \(a\) e \(b\) sono le lunghezze dei semiassi dell'ellisse che si ottiene nelle sezioni orizzontali, mentre \(c\) è un parametro che determina l'apertura del parabolide.
  
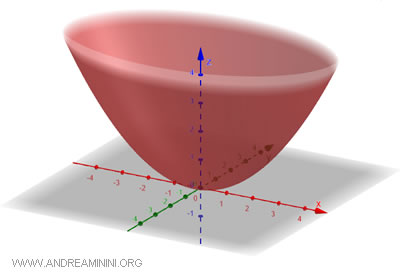
  E' detto "ellittico" perché se interseco un piano con il parabolide, la sezione orizzontale è un'ellisse.
  
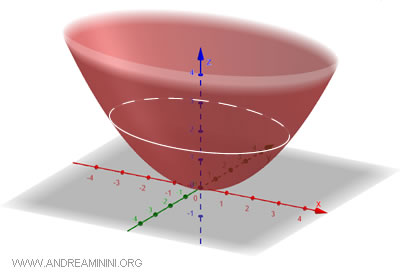
  In particolare, se \(a = b\), l'equazione si riduce a quella di un "paraboloide di rivoluzione": $$ x^2 + y^2 = 2pz $$ Dove \(p\) è un parametro legato all'apertura del parabolide.
  
  

  Un esempio pratico è la parabola satellitare che utilizza la forma ellittica per raccogliere e focalizzare il segnale trasmesso dallo spazio. In particolar modo, la parabola di rotazione è molto utile perché può riflettere i raggi paralleli verso un singolo punto focale, quindi può far convergere una maggiore quantità di informazioni verso un unico punto. E' una proprietà ottica molto utile nella realizzazione di antenne e telescopi.

• Parabolide iperbolico
  La superficie si ottiene traslando una parabola lungo una direzione che non è parallela al suo asse simmetrico. Il risultato è una forma in cui le sezioni orizzontali sono iperboliche, mentre quelle verticali rimangono paraboliche. L'equazione generale di un parabolide iperbolico è $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \frac{z}{c} $$ Dove \(a\) e \(b\) sono parametri che determinano l'estensione dell'iperbole nelle sezioni orizzontali, mentre \(c\) determina l'apertura del parabolide.
  
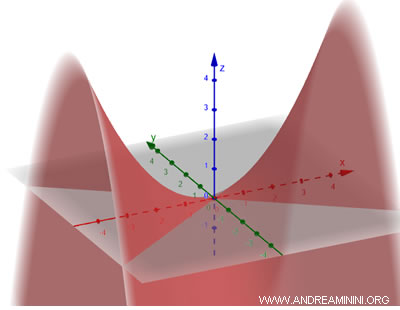
  In questo caso è detto "iperbolico" perché se interseco un piano con il parabolide, la sezione orizzontale è un'iperbole.
  

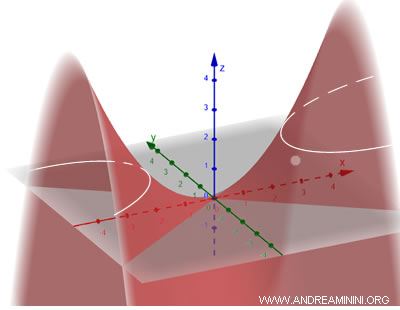
  Un esempio è l'uso dei parabolidi iperbolici in architettura per realizzare tetti curvi agli edifici e distribuire il peso della copertura in modo ottimale.

In entrambi i casi le sezioni verticali sono delle parabole. Per questa ragione queste forme sono dette "parabolidi".

In conclusione, pur derivando entrambi dalla parabola, questi due tipi di parabolidi si differenziano per forma e applicazioni.

E così via.