Ellissoide

Un ellissoide è una figura geometrica tridimensionale che si può immaginare come una versione allungata o schiacciata di una sfera.

In altre parole, è una superficie liscia e chiusa, simile a una sfera, ma con proporzioni diverse lungo i suoi assi x, y, z.

Un ellissoide si ottiene facendo ruotare una ellisse attorno a uno dei suoi assi di simmetria.

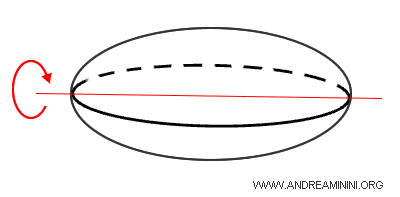
A sua volta, l'ellisse è una figura simile a un cerchio, ma con due assi di lunghezza diversa: uno più lungo e uno più corto.

Quando questa rotazione avviene, si genera una forma che ha tre dimensioni: altezza, larghezza e profondità.

L'equazione dell'ellissoide

Dal punto di vista matematico l'equazione di un ellissoide è la seguente:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$

Dove \(x\), \(y\) e \(z\) rappresentano le coordinate nello spazio dei punti che si trovano sulla superficie dell'ellissoide.

Le lettere \(a\), \(b\) e \(c\) rappresentano le lunghezze dei tre semiassi, che determinano la forma dell'ellissoide.

Questi semiassi sono come i raggi di una sfera, ma anziché essere tutti uguali, possono avere lunghezze diverse. L'equazione è la seguente:

Un esempio pratico

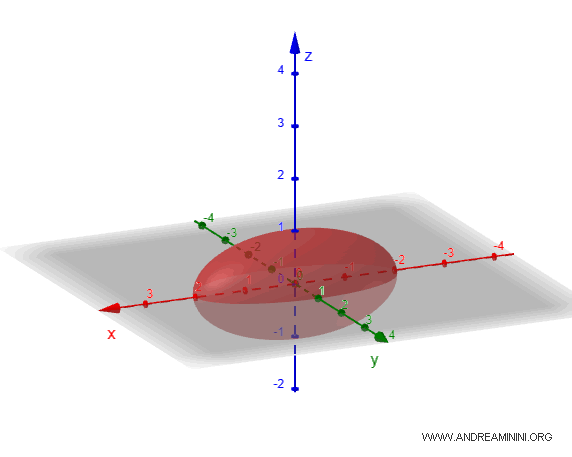
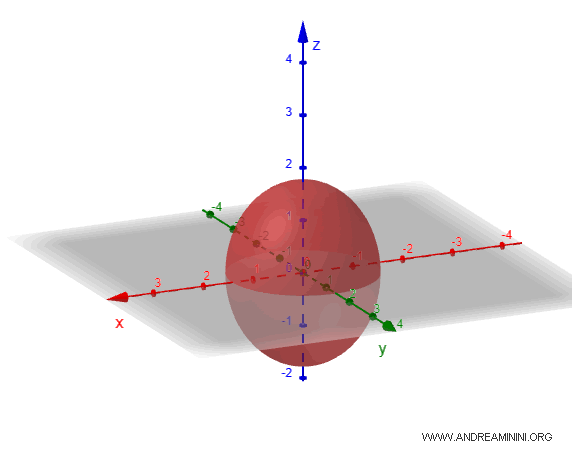
Considero un ellissoide in cui i semiassi sono $ a=2 $, $ b=1 $ e $ c =1 $

L'equazione dell'ellissoide è la seguente:

$$ \frac{x^2}{2^2} + \frac{y^2}{1} + \frac{z^2}{1} = 1 $$

$$ \frac{x^2}{4} + y^2 + z^2 = 1 $$

Se rappresento graficamente questo solido, l'ellissoide appare come una sfera allungata e schiacciata.

Tipi di ellissoidi

Ci sono diversi tipi di ellissoidi, a seconda di come sono disposti i loro semiassi:

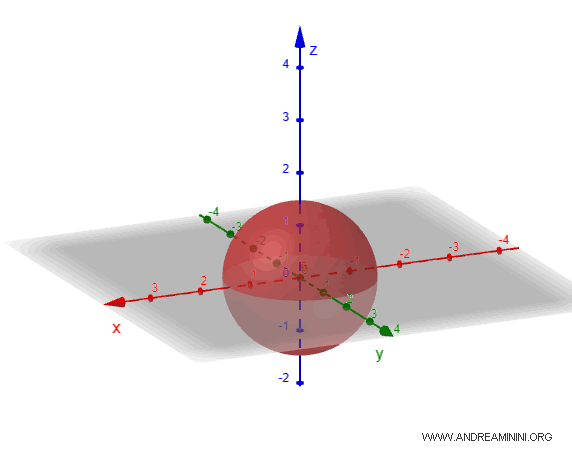
• Ellissoide sferico
  Se i tre semiassi \(a\), \(b\) e \(c\) sono tutti uguali, l'ellissoide diventa una sfera perfetta. In questo caso, la figura è simmetrica in tutte le direzioni e ogni piano che passa per il centro della sfera crea un cerchio perfetto.
  
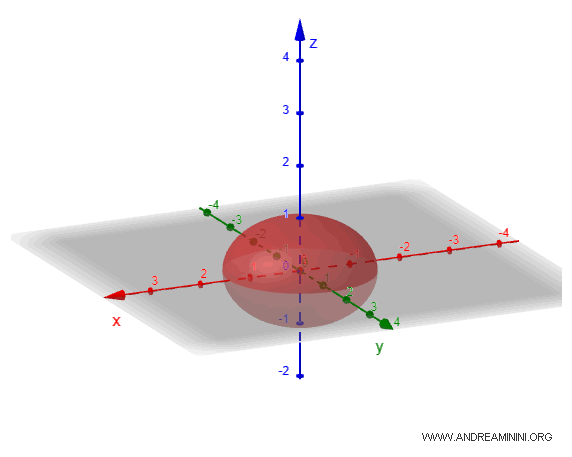
• Ellissoide oblato
  Questo tipo di ellissoide si ottiene quando due dei semiassi, diciamo \(a\) e \(b\), sono uguali, mentre il terzo, \(c\), è più corto. Questa forma è schiacciata ai poli, come un disco appiattito. Un esempio concreto di ellissoide oblato è la Terra, che non è una sfera perfetta ma è leggermente schiacciata ai poli a causa della rotazione.
  
• Ellissoide prolato
  In questo caso, due semiassi, \(a\) e \(b\), sono uguali, ma il terzo, \(c\), è più lungo. Questo tipo di ellissoide è allungato lungo un asse, simile a una pallone da rugby. Si può immaginare come una sfera allungata lungo una direzione specifica.
  

Nota. Gli ellissoidi non sono solo concetti astratti: trovano applicazioni pratiche in molti campi. . In astronomia, gli ellissoidi aiutano a descrivere la forma di alcuni corpi celesti, come i pianeti o le stelle che non sono perfettamente sferici a causa della loro rotazione. Ad esempio, per rappresentare la forma reale della Terra si utilizza un ellissoide oblato.

In sintesi, un ellissoide è una figura geometrica che estende il concetto di sfera per adattarsi a una varietà di forme naturali e artificiali che incontriamo nel mondo e nell'universo.