Equazione dell'ellisse

L'equazione dell'ellisse in un sistema di coordinate cartesiane centrato nel punto medio dei due fuochi (il centro dell'ellisse) è: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ Con $ a>0 $ e $ b > 0 $

Dove x e y sono le coordinate di un punto P(x;y) qualsiasi dell'ellisse

• \(a\) è il semiasse orizzontale, la distanza dal centro all'estremità più lontana dell'ellisse sull'asse orizzontale
• \(b\) è il semiasse verticale, la distanza dal centro all'estremità più vicina sull'asse verticale.

Questa equazione è detta "equazione standard" dell'ellisse si può applicare sia quando l'asse maggiore è orizzontale che verticale.

Se l'ellisse è centrata nel punto \((h, k)\) invece che nell'origine, l'equazione dell'ellisse diventa:

$$ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 $$

In generale un'ellisse è definita come il luogo dei punti per i quali la somma delle distanze da due punti fissi, detti fuochi, è costante.

Nota. Nell'equazione dell'ellisse i coefficienti devono essere maggiori di zero $ a>0 $ e $ b>0 $ poiché rappresentano le lunghezze dei semiassi dell'ellisse. Inoltre, il termine noto deve essere positivo e uguale a 1. Se il termine noto fosse diverso da 1, si potrebbe comunque ottenere un'equazione equivalente dividendo tutti i termini per quel valore.

Gli assi, i vertici, i fuochi e l'eccentricità dell'ellisse

La relazione d'ordine tra \( a \) e \( b \) indica se l'asse maggiore è orizzontale o verticale.

• Se a > b l'asse maggiore è orizzontale (asse x)
• Se a < b l'asse maggiore è verticale (asse y)
• Se a = b l'asse maggiore e minore sono uguali, quindi l'ellisse diventa un cerchio.

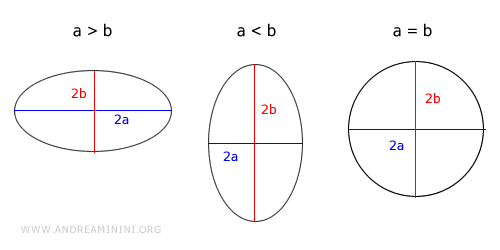
Le coordinate dei fuochi dell'ellisse cambiano a seconda se l'asse maggiore è orizzontale (a>b) o verticale (a<b).

• Se a>b $$ F_1 ( - \sqrt{ a^2 - b^2 } ;0 ) $$ $$ F_2 ( \sqrt{ a^2 - b^2 } ;0 ) $$
• Se a<b $$ F_1 (0; - \sqrt{ b^2 - a^2 } ) $$ $$ F_2 ( 0; \sqrt{ b^2 - a^2 } ) $$

Dove "a" e "b" sono le lunghezze dei semiassi dell'ellisse.

I termini $ \sqrt{a^2-b^2} $ e $ \sqrt{b^2-a^2} $ misurano la metà della distanza focale (2c), ossia la distanza di ogni fuoco dal centro (O) ovvero  $ c = \overline{OF_1} =  \overline{OF_2} $.

• Se a>b $$  c=\sqrt{a^2-b^2} $$
• Se a<b $$ c= \sqrt{ b^2 - a^2 } $$

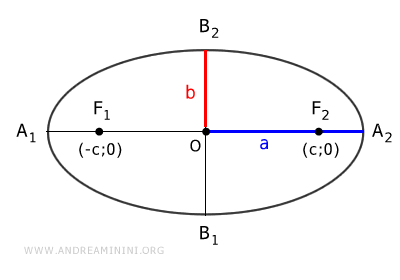
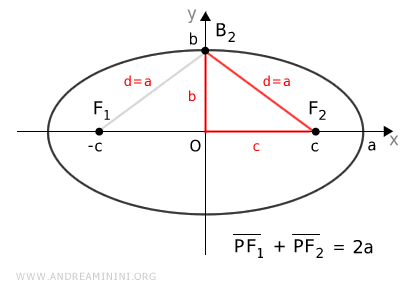
Dimostrazione. Vediamo di capire perché $ c = \sqrt{ a^2 - b^2 } $. In un ellisse la somma delle distanze di un punto P dai fuochi è costante $$ \overline{PF_1} + \overline{PF_2} = k $$ Prendo in considerazione solo il caso di un ellisse orizzontale ma lo stesso ragionamento vale anche per un ellisse verticale. Il punto $ A_2 $ è un vertice dell'ellisse sull'asse maggiore.

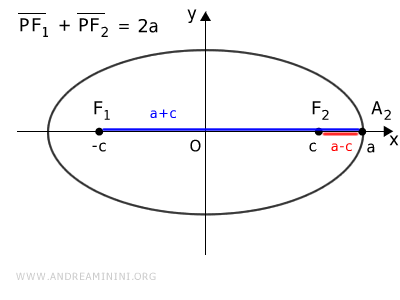
E' un punto dell'ellisse e la somma delle distanze dai fuochi è costante. $$ \overline{A_2F_1} + \overline{A_2F_2} = k $$ Sapendo che le distanze sono $ \overline{A_2F_1} = a+c $ e $ \overline{A_2F_2} = a-c $, sostituisco queste espressioni nell'equazione $$ (a+c) + (a-c) = k $$ $$ \require{cancel} a+ \cancel{c} + a -\cancel{c}  = k $$ $$ 2a = k $$ Quindi, se la somma delle distanze dai fuochi è $ k=2a $ per il punto $ A_2 $, deduco che lo sia anche per qualsiasi altro punto dell'ellisse $$ \overline{PF_1} + \overline{PF_2} = 2a $$ Ora prendo in considerazione il vertice $ B_2 $ sull'asse minore.

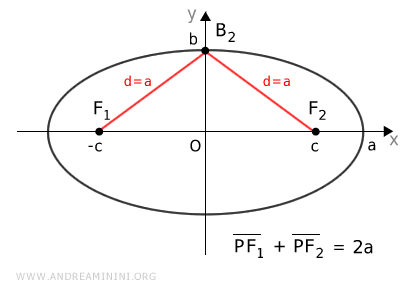
Misuro la somma delle distanze da $ B_2 $ ai fuochi. $$ \overline{B_2F_1} + \overline{B_2F_2} = 2a $$ Poiché $ B_2 $ si trova sull'asse di simmetria, deduco che la distanza sia dai fuochi sia la stessa. $ \overline{B_2F_1} = \overline{B_2F_2} = a $. Pertanto, il segmento $ B_2 F_2 = a $. Una volta capito questo, per ottenere la distanza focale $ c = \overline{OF_2} $ basta applicare il teorema di Pitagora sul triangolo $OB_2F_2 $ ovvero $ c = \sqrt{a^2-b^2} $

Le coordinate dei vertici dell'ellisse sono i punti di intersezione dell'ellisse con gli assi e sono  le seguenti:

$$ A_1 ( -a; 0) $$

$$ A_2 ( a; 0) $$

$$ B_1 ( 0; -b) $$

$$ B_2 ( 0; b) $$

L'eccentricità (e) è un parametro che misura quanto l'ellisse si discosta da una forma circolare ed è determinata dal rapporto tra la distanza focale (2c) e la lunghezza dell'asse maggiore (2a oppure 2b).

$$ e = \frac{\text{distanza focale} }{ \text{lunghezza asse maggiore} } $$

Quindi, la formula dell'eccentricità cambia a seconda se l'ellisse è orizzontale o verticale.

• Se a>b la formula dell'eccentricità è $$ e = \frac{c}{a} = \frac{ \sqrt{a^2-b^2} }{a} = \sqrt{ 1 - \frac{b^2}{a^2}  } $$
• Se a<b la formula dell'eccentricità è $$ e = \frac{c}{b}  = \frac{ \sqrt{b^2-a^2} }{b} = \sqrt{ 1 - \frac{a^2}{b^2}  }  $$
• Se a=b si può usare indiferentemente una delle precedenti formule

L'eccentricità è un parametro compreso tra 0 e 1.

$$ 0 \le e < 1 $$

Quando l'eccentricità è nulla (e=0) i due fuochi coincidono nello stesso punto e l'ellisse degenera in un cerchio.

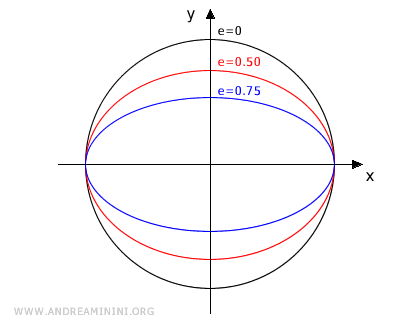
Viceversa, l'ellisse è molto schiacciata sull'asse maggiore quando il parametro "e" si avvicina a 1.

Nota. Nel caso limite in cui l'eccentricità è e=1 l'ellisse coincide con l'asse maggiore e si parla di ellisse degenere.

Ogni ellisse possiede due fuochi e due rette direttrici, simmetriche e perpendicolari rispetto all'asse focale.

Se l'asse focale coincide con l'asse \(x\), le rette direttrici si esprimono come:

$$ x = \pm \frac{a^2}{c} $$

Nel caso in cui l'asse focale sia l'asse \(y\), le rette direttrici sono date da:

$$ y = \pm \frac{b^2}{c} $$

In generale, per qualsiasi conica, dato un punto \( P(x;y) \) sull'ellisse, il rapporto tra la distanza \( \overline{PF} \) del punto dal fuoco e la distanza \( \overline{PH} \) del punto dalla direttrice è costante e corrisponde all'eccentricità dell'ellisse:

$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$

Ecco un esempio delle rette direttrici di un'ellisse.

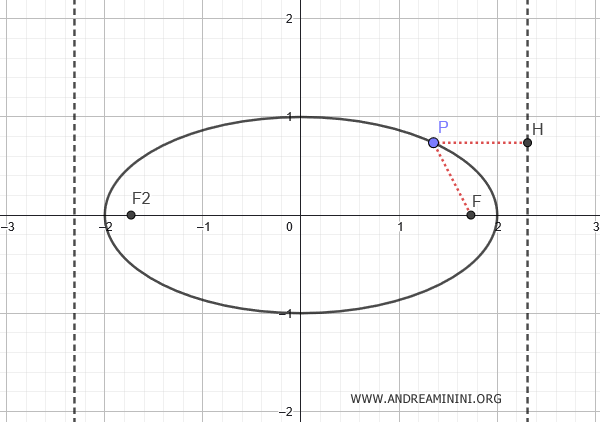
Dimostrazione. Considero un'ellisse con l'asse focale sull'asse x. $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ Una retta direttrice è perpendicolare all'asse x  che passa per il punto $ F(c;0) $ $$ x = k $$ Per definizione, il rapporto la distanza tra un punto dell'ellisse e il fuoco e la distanza tra lo stesso punto e la retta direttrice è costante ed è uguale all'eccentricità. $$ \frac{ \overline{PF} }{ \overline{PH} } = e $$ Dove l'eccentricità è il rapporto $ e=\frac{c}{a} $ $$ \frac{ \overline{PF} }{ \overline{PH} } = \frac{c}{a} $$ Scelgo come punto $ P $ il vertice $ A(a,0) $ dell'ellisse. Quindi la distanza $ \overline{PF} = a-c $ mentre la distanza $ \overline{PH} = k-a $ $$ \frac{ a-c }{ k-a } = \frac{c}{a} $$ $$ a \cdot (a-c)= c \cdot (k-a) $$ $$ \require{cancel} a^2 - \cancel{ac} = ck - \cancel{ac} $$ $$ a^2 = ck $$ $$ k = \frac{a^2}{c} $$ Poiché l'altra retta direttrice è simmetrica, le due rette direttrici si trovano sull'asse x nel punto $ (k;0) $ e $ (-k;0) $.

Per trovare le intersezioni con gli assi cartesiani metto a sistema l'equazione dell'ellisse ponendo x=0 e poi y=0.

$$ \begin{cases} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \\ x=0 \end{cases} $$

Quando l'ellisse è centrata all'origine la soluzione del sistema è $ x = \pm a $ cioé i vertici $ A_1(-a;0) $ e $ A_2(a;0) $.

$$ \begin{cases} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \\ y =0 \end{cases} $$

Quando l'ellisse è centrata all'origine la soluzione di quest'altro sistema è $ y = \pm b $ cioé i vertici $ B_1(-b;0) $ e $ B_2(b;0) $.

Un esempio pratico

Considero l'equazione generale di un'ellisse centrata nell'origine con gli assi principali allineati con gli assi cartesiani:

$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$

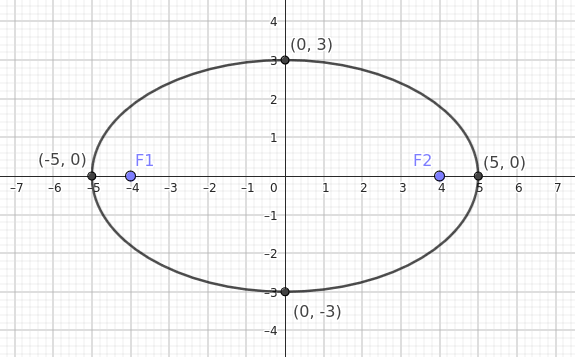
In questo caso la lunghezza degli assi è \( a = 5 \) e \( b = 3 \).

Poiché $ a>b $ l'asse maggiore è l'asse orizzontale x.

L'ellisse ha i due vertici principali sull'asse \( x \) a \(( \pm a, 0 ) = ( \pm 5, 0 )\) e i due vertici minori sull'asse \( y \) a \(( 0, \pm b ) = (0, \pm 3) \).

• L'asse maggiore è la distanza tra i due vertici principali ed è \( 2a = 2 \cdot 5 = 10 \).
• L'asse minore è la distanza tra i due vertici minori ed è \( 2b = 2 \cdot 3 = 6 \).

Il centro dell'ellisse è l'origine degli assi.

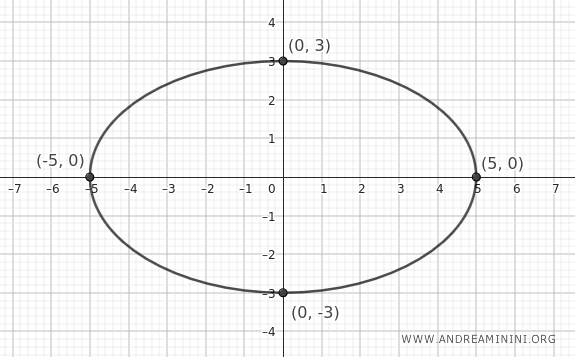
La distanza dei fuochi dal centro è data determinata dalla metà della distanza focale \( c \)

$$ c = \sqrt{a^2 - b^2} $$

$$ c = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4 $$

Quindi, i I fuochi si trovano a \(( \pm c, 0 )\), ovvero nei punti \(( \pm 4, 0 )\).

L'eccentricità \( e \) dell'ellisse è data da \( e = \frac{c}{a} \).

$$ e = \frac{4}{5} = 0.8 $$

L'asse focale dell'ellise è l'asse x. Quindi, le rette direttrici dell'ellisse sono le seguenti:

$$ x = \pm \frac{a^2}{c} = \pm \frac{25}{4}  \approx \pm 6.25 $$

Se prendo un qualsiasi punto $ P(x;y) $ dell'ellisse, il rapporto tra le distanze $ \frac{ \overline{PF} }{ \overline{PH} } = e $ è costante e coincide con l'eccentricità dell'ellisse.

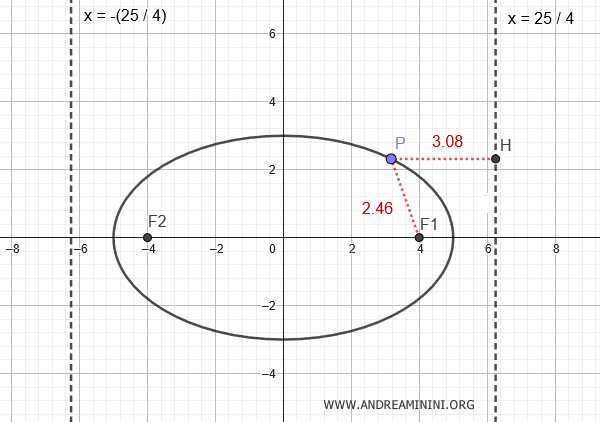
Ad esempio, nel punto $ P $ la distanza tra il punto e il fuoco è $ \overline{PF} = 2.46 $ mentre la distanza tra il punto e la retta direttrice è 4 \overline{PH} = 3.08 $.

Il rapporto tra le due distanze è uguale all'eccentricità dell'ellisse.

$$ \frac{ \overline{PF} }{ \overline{PH} } =  \frac{2.46}{3.08} = 0.8 = e $$

Lo stesso vale prendendo qualsiasi altro punto dell'ellisse.

Questo completa lo studio dell'ellisse.

Note a margine

Alcune osservazioni e note e margine sull'equazione dell'ellisse

• L'equazione dell'ellisse non è una funzione perché per ogni valore della variabile indipendente x, fatta eccezione per i vertici dell'asse orizzontale (A₁ e A₂), restituisce due valori della variabile dipendente y. $$ y^2 = b^2 \cdot (1 - \frac{x^2}{a^2})  $$ $$ \sqrt{y^2} = \sqrt{ \frac{b^2}{a^2} \cdot (a^2 - x^2)}  $$ $$ y = \pm  \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2}  $$ L'equazione dell'ellisse si può considerare come l'unione di due funzioni. $$ y =  \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2}  $$ e $$ y =  - \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2}  $$

E così via.