L'equazione della parabola

L'equazione di una parabola in forma standard con l'asse di simmetria parallelo all'asse y è la seguente: $$ y = ax^2 + bx + c $$ Dove a,b e c sono coefficienti reali costanti con a diverso da zero (a≠0).

Il coefficiente "a" è particolarmente utile nello studio di una parabola.

Il valore assoluto |a| del coefficiente "a" determina l'apertura della parabola. Quanto maggiore è il valore |a|, tanto minore è l'apertura della parabola rispetto al proprio asse.

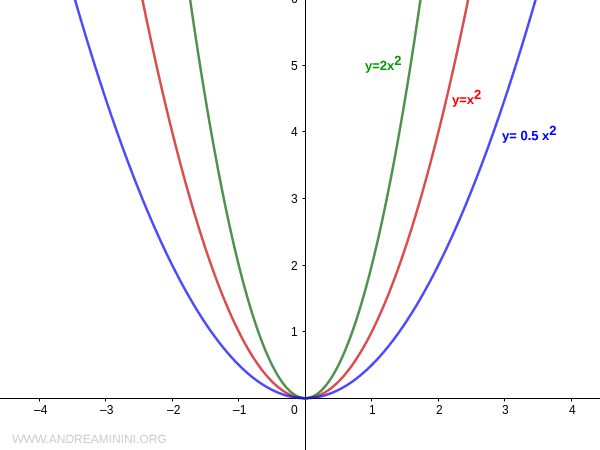
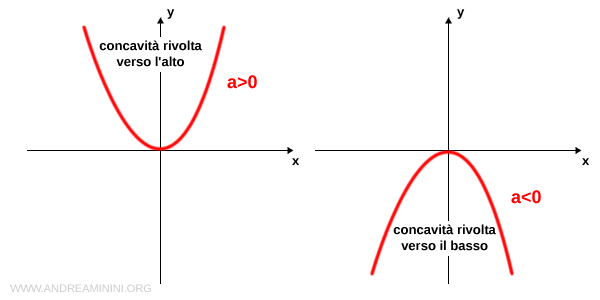
Inoltre, il segno del coefficiente "a" determina anche la concavità o convessità della parabola.

• Se a>0 la parabola è rivolta verso l'alto (convessa)
• Se a<0 la parabola è rivolta verso il basso (concava).

Quando l'asse di simmetria della parabola è orizzontale, l'equazione standard della parabola si scrive in quest'altro modo: $$ x = ay^2 + by + c $$

Le principali componenti di una parabola sono le seguenti

• Fuoco
  Il fuoco \( F \) è un punto fisso all'interno della parabola. Le coordinate del fuoco si ottengono come segue:
  \[ F \begin{pmatrix} -\frac{b}{2a}, \frac{1-Δ}{4a} \end{pmatrix} \] dove \( a \), \( b \) e \( c \) sono i coefficienti dell'equazione della parabola \( y = ax^2 + bx + c \), e il discriminante è \( Δ = b^2 - 4ac \).
• Direttrice
  La direttrice \( d \) è una retta fissa esterna alla parabola. L'equazione della direttrice è la seguente: $$ y= - \frac{1+\Delta}{4a} $$
• Asse
  L'asse di una parabola è una retta perpendicolare alla retta direttrice \( d \), che passa per il fuoco \( F \). Questo asse funge anche da asse di simmetria, dividendo la parabola in due parti speculari. L'equazione dell'asse è data da: $$ x = - \frac{b}{2a} $$
• Il vertice
  Il vertice \( V \) è il punto in cui la parabola interseca l'asse di simmetria. In corrispondenza del vertice, la parabola raggiunge il suo valore massimo o minimo, a seconda del segno del coefficiente \( a \) nell'equazione della parabola \( y = ax^2 + bx + c \). Le coordinate del vertice si possono calcolare come segue: \[ V \left( -\frac{b}{2a} , -\frac{\Delta}{4a} \right) \] dove \(\Delta = b^2 - 4ac\) è il discriminante.

Casi particolari dell'equazione della parabola

L'equazione della parabola $ y= ax^2+bx+c $ può assumere alcuni casi particolari quando i coefficienti b e/o c sono nulli.

• Se $ b=0 $ l'equazione diventa $ y=ax^2+c $ e l'asse della parabola coincide con l'asse y.
  
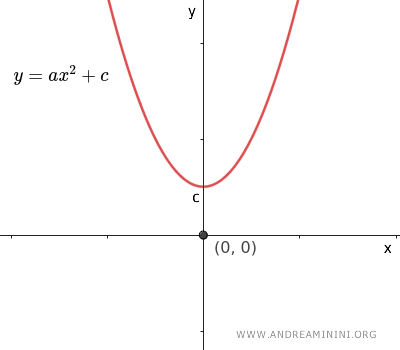
• Se $ c=0 $ l'equazione diventa $ y=ax^2+bx $ e il grafico della parabola passa sempre per l'origine O(0;0) degli assi cartesiani, perché la variabile indipendente x=0 rende nulla la variabile dipendente y=0.
  
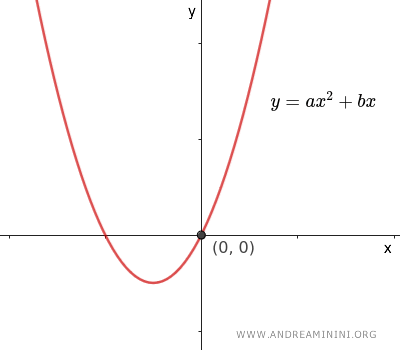
• Se $ b=0 $ e $ c=0 $ l'equazione diventa $ y =ax^2 $, l'asse della parabola coincide con l'asse y e il vertice della parabola con l'origine O(0;0) degli assi cartesiani.
  

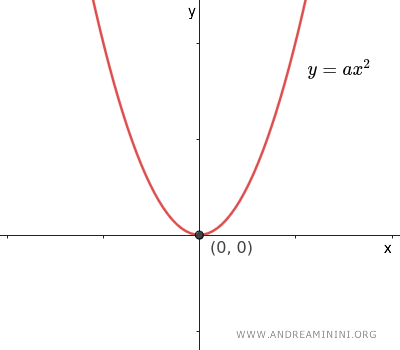
Equazione della parabola con asse sulle ordinate (y) e vertice nell'origine

L'equazione della parabola con l'asse che coincide con l'asse y e il vertice nell'origine degli assi cartesiani è la seguente $$ y = ax^2 $$ Dove il coefficiente $ a \ne 0 $ è diverso da zero.

In questo caso, l'asse della parabola è semplicemente:

$$ x = 0 $$

Il fuoco F si trova alle coordinate

$$ F \left(0; \frac{1}{4a} \right) $$

L'equazione della direttrice è:

$$ y = - \frac{1}{4a} $$

Nota. L'equazione della parabola con asse coincidente sulle ordinate (y) e vertice sull'origine ha tutti i valori non negativi se il coefficiente a>0. In questo caso anche il fuoco è positivo e la concavità della parabola è verso l'alto. Viceversa, ha tutti i valori non positivi se a<0. In quest'altro caso il fuoco è negativo e la concavità della parabola è verso il basso.

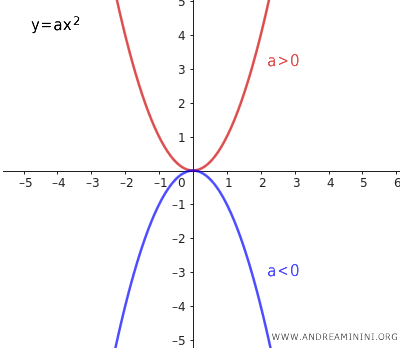
Due parabole sono "parabole simmetriche" quando hanno il coefficiente "a" opposto. Ad esempio $ y = \frac{1}{8} x^2 $ e $ y = - \frac{1}{8} x^2 $ sono parabole simmetriche. Le parabole simmetriche sono anche congruenti. Nel caso particolare in cui a=0 non si ottiene la parabola perché la curva degenera in una retta y=0 che coincide con l'asse delle x. In questi casi si parla di "parabola degenere".

Esempio

In questo esempio considero la parabola

$$ y = \frac{1}{8} x^2 $$

Il coefficiente $ a = \frac{1}{8} $ , quindi il fuoco della parabola si trova alle coordinate seguenti:

$$ F \left(0; \frac{1}{4a} \right)  $$

$$ F \left(0; \frac{1}{4 \cdot \frac{1}{8}} \right)  $$

$$ F \left(0; \frac{1}{\frac{1}{2}} \right)  $$

$$ F (0; 2) $$

L'equazione della retta direttrice, invece, è la seguente

$$ y = - \frac{1}{4a} $$

$$ y = - \frac{1}{4 \frac{1}{8} } $$

$$ y = - \frac{1}{ \frac{1}{2} } $$

$$ y = - 2 $$

Ecco il grafico della parabola.

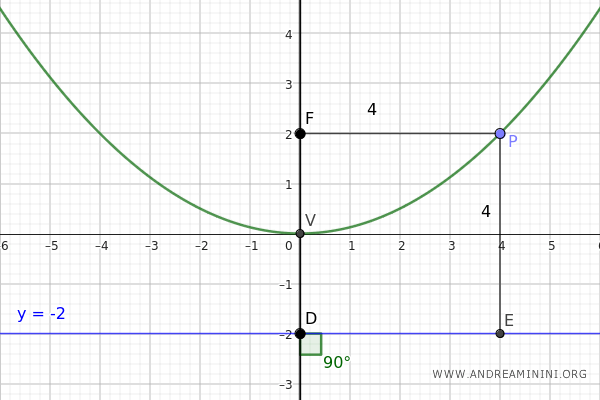
Dimostrazione

Considero come ipotesi iniziale l'asse della parabola coincidente con l'asse y e il vertice V della parabola sull'origine degli assi cartesiani.

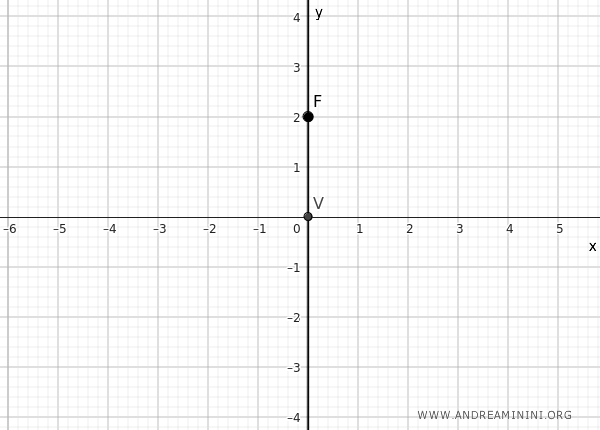
Il fuoco F è un punto dell'asse della parabola, quindi in questo caso è un punto dell'asse y.

In una parabola la distanza tra il fuoco e un punto della parabola è uguale alla distanza tra la direttrice e il punto stesso.

In questo caso il punto V è l'unico punto della parabola che conosco, ma posso dedurre che la distanza VF≅OD dove D è un punto della retta direttrice.

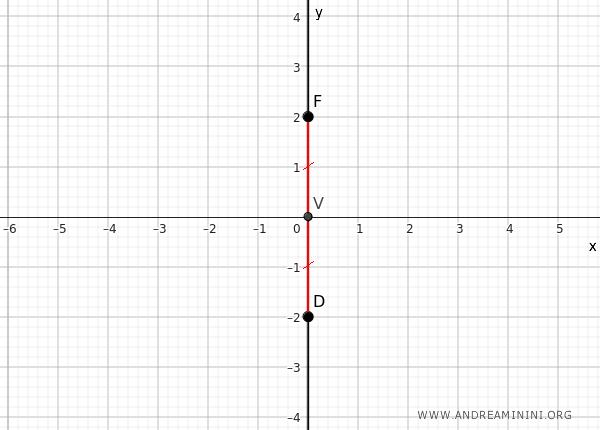
Sapendo che la retta direttrice è sempre perpendicolare all'asse della parabola, deduco che in questo caso la retta direttrice è parallela all'asse x e passa per il punto D.

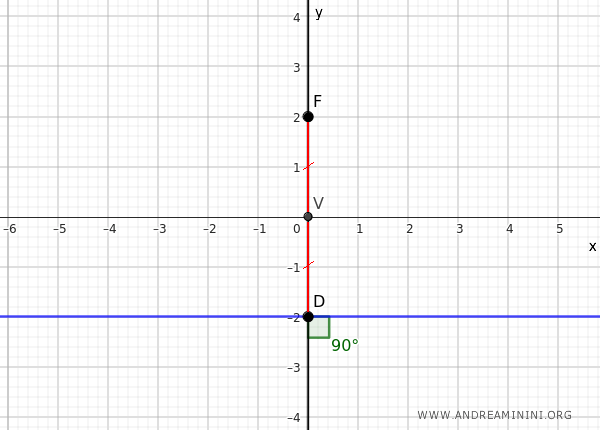
Pertanto, l'equazione della retta direttrice è

$$ y = -f $$

Dove f=VD=VF per costruzione poiché VD=VF.

A questo punto prendo un punto P qualsiasi della parabola.

Per definizione la distanza PF tra il punto e il fuoco deve essere uguale alla distanza PE tra il punto e la direttrice, ovvero PF=PE

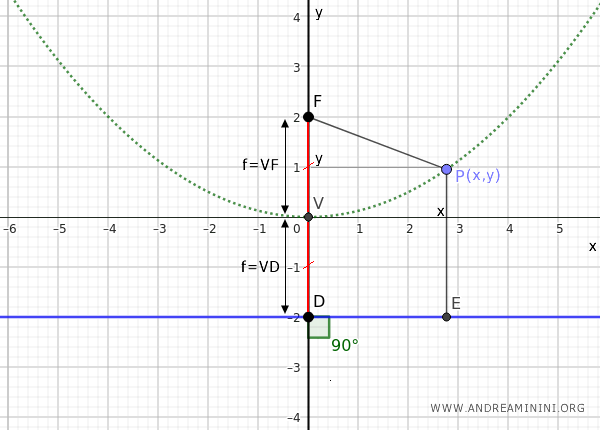
Il segmento PF è congruente al segmento PE

$$ \overline{PF} = \overline{PE} $$

Il segmento PF posso scriverlo come distanza euclidea tra due punti $ \overline{PF} = \sqrt{ x^2 + (f-y)^2 }$ dove f=VF.

$$  \sqrt{ x^2 + (f-y)^2 } = \overline{PE} $$

Il segmento PE posso, invece, scriverlo come la somma $ \overline{PE} = | y + f | $ dove f=VD.

$$  \sqrt{ x^2 + (f-y)^2 } = | y+f | $$

Applico la proprietà invariantiva delle equazioni ed elevo entrambi i lati dell'equazione al quadrato

$$ \left(  \sqrt{ x^2 + (f-y)^2 } \right)^2 = ( | y+f | )^2 $$

$$ x^2 + (f-y)^2  = ( y+f )^2 $$

$$ \require{cancel} x^2 + \cancel{f^2} -2fy + \cancel{y^2}  = \cancel{y^2} + 2fy + \cancel{f^2} $$

$$ x^2  -2fy -2fy  = 0  $$

$$ x^2  -4fy  = 0  $$

Questo mi permette di ricavare y e ottenere l'equazione della parabola

$$ y = \frac{1}{4f} x^2 $$

Ponendo il coefficiente $ a= \frac{1}{4f} $ l'equazione diventa:

$$ y = a  x^2 $$

Certo, ecco una versione migliorata del testo:

Poiché \( f \ne 0 \) per evitare una divisione per zero, ne deduco che \( a \ne 0 \). Di conseguenza, il coefficiente \( a \) deve essere sempre diverso da zero.

Dalla relazione $ a= \frac{1}{4f} $ posso ricavare anche la componente y=f delle coordinate del fuoco F(x,y)

$$ f = \frac{1}{4a} $$

In questo caso l'asse della parabola coincide con l'asse y, quindi la componente x=0 del fuoco è nulla.

Pertanto, il fuoco si trova a queste coordinate del piano cartesiano

$$ F(x,y) = \left(  0 \ , \ \frac{1}{4a}  \right) $$

Infine, sapendo che la retta direttrice è

$$ y = -f $$

Sostituisco $ f=\frac{1}{4a} $ e ottengo l'equazione completa della retta direttrice.

$$ y = -\frac{1}{4a} $$

In questo modo ho dimostrato tutte le formule dell'equazione della parabola con l'asse corrispondente alle ordinate e il vertice nell'origine degli assi cartesiano.

Equazione della parabola con asse parallelo alle ordinate (y)

L'equazione della parabola con l'asse parallelo all'asse y e il vertice in un punto qualsiasi del piano è la seguente con il coefficiente $ a \ne 0 $ è diverso da zero. $$ y = ax^2 + bx + c $$ In alternativa, l'equazione della parabola può essere scritta nella forma generale dove (h,k) è il vertice $$ y =a (x-h)^2 + k $$ oppure nella forma standard dove p è la distanza dal fuoco al vertice $$ (x-h)^2 = 4p(y-k)  $$

Ogni parabola $ y= ax^2 +bx+c   $  con l'asse parallelo all'asse y e vertice nel punto $ V (x_v; y_v ) $ si ottiene tramite la traslazione di una parabola $ y = ax^2 $ con vertice nell'origine e asse coincidente con le ordinate.

$$ y - y_v = a(x - x_v)^2 $$

L'asse della parabola è:

$$ x = - \frac{b}{2a} $$

Il vertice della parabola si trova alle seguenti coordinate

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{Δ}{4a} \end{pmatrix} $$

Dove a,b,c sono i coefficienti dell'equazione della parabola y=ax²+bx+c e il discriminante Δ=b²-4ac

Il fuoco F si trova alle coordinate

$$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1-Δ}{4a} \end{pmatrix} $$

L'equazione della direttrice è:

$$ y= - \frac{1+Δ}{4a} $$

Nota. A ogni equazione del tipo $ y=ax^2+bx+c $ con $ a \ne 0 $ corrisponde una parabola con l'asse parallelo alle y e viceversa. Questo perché le parabole con l'asse parallelo all'asse y sono semplici traslazioni delle parabole y=ax² con l'asse coincidente all'asse y.

Esempio

Considero la seguente parabola

$$ y = 2x^2 - 4x- 1 $$

Il vertice della parabola si trova alle coordinate V dove a=2, b=-4, c=-1 e il discriminante è $  Δ=b^2- 4ac $

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{Δ}{4a} \end{pmatrix} $$

$$ V \begin{pmatrix} - \frac{b}{2a} \ , \ - \frac{b^2-4ac}{4a} \end{pmatrix} $$

$$ V \begin{pmatrix} - \frac{-4}{2 \cdot (2)} \ , \ - \frac{(-4)^2-4 \cdot 2 \cdot (-1) }{4 \cdot 2} \end{pmatrix} $$

$$ V \begin{pmatrix}  \frac{4}{4} \ , \ - \frac{16+8 }{8} \end{pmatrix} $$

$$ V \begin{pmatrix}  1 \ , \ - \frac{24}{8} \end{pmatrix} $$

$$ V \begin{pmatrix}  1 \ , \ - 3 \end{pmatrix} $$

La retta direttrice è la seguente sapendo già che Δ=b²-4ac=24 e a=2:

$$ y= - \frac{1+Δ}{4a} $$

$$ y= - \frac{1+24}{4 \cdot 2} $$

$$ y= - \frac{25}{8} $$

Il fuoco si trova alle coordinate sapendo già che Δ=b²-4ac=24, a=2 e b=-4:

$$ F \begin{pmatrix} - \frac{b}{2a} \ , \ \frac{1-Δ}{4a} \end{pmatrix} $$

$$ F \begin{pmatrix} - \frac{-4}{2 \cdot 2} \ , \ \frac{1-24}{4 \cdot 2} \end{pmatrix} $$

$$ F \begin{pmatrix} 1 \ , \ \frac{-23}{8} \end{pmatrix} $$

Per una conferma visualizzo il grafico della parabola ed effettivamente ogni punto della parabola si trova alla stessa distanza tra il fuoco F e la retta direttrice.

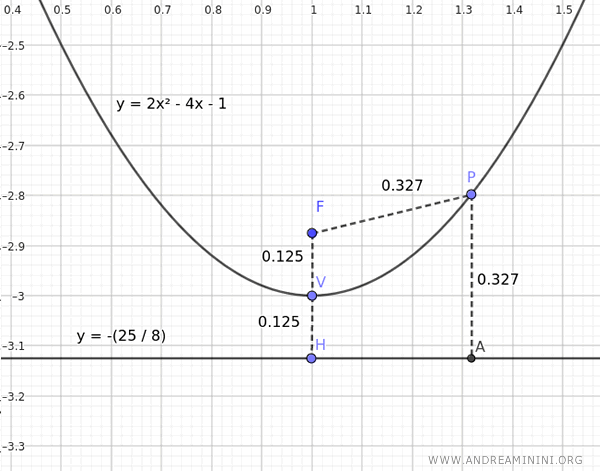
Nota. La distranza tra l'origine O(0;0) degli assi cartesiani e il vertice della parabola $ V \begin{pmatrix}  1 \ , \ - 3 \end{pmatrix} $ è il vettore $ \vec{v} =\begin{pmatrix}  1 \ , \ - 3 \end{pmatrix} $

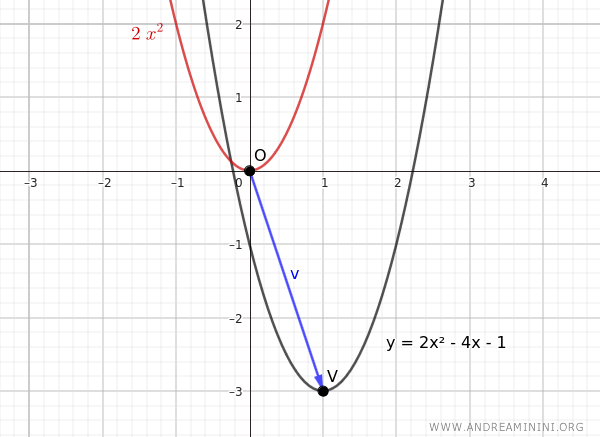
Pertanto, posso dimostrare che la parabola $ y=2x^2 -4x-1  $ è la traslazione di un'altra parabola passante per l'origine $ y = 2x^2 $ che ha lo stesso coefficiente $ a =2 $. $$ y - y_v = a(x - x_v)^2 $$ $$ y - y_v = 2(x - x_v)^2 $$ In questo caso, le componenti del vertice V(1,-3) sono x_v = 1 e y_v=-3 $$ y - (-3) = 2(x - 1)^2 $$ $$ y + 3 = 2(x-1)^2 $$ $$ y  = 2(x-1)^2 -3 $$ $$ y  = 2(x^2-2x+1) -3 $$ $$ y  = 2x^2-4x+2 -3 $$ $$ y  = 2x^2-4x-1 $$ Questo conferma che la parabola $ y=2x^2 -4x-1  $ è la traslazione della parabola passante per l'origine $ y = 2x^2 $ Queste due parabole sono congruenti perché possono essere sovrapposte punto a punto dopo un movimento rigido, ovvero un movimento isometrico che non causa nessuna deformazione.

Dimostrazione

Per dimostrare l'equazione $ y=ax^2+bx+c $ parto dalla seguente ipotesi:

Ogni parabola con l'asse parallelo all'asse y sono una traslazione di una parabola $ y=ax^2 $ con l'asse coincidente all'asse y.

$$ y = ax^2 $$

In generale, la traslazione di un punto qualsiasi $ (x;y) \rightarrow (x';y') $ del piano si ottiene tramite la seguente operazione di isometria:

$$ \begin{cases} x' = x+ x_v \\ \\ y' = y+ y_v \end{cases} $$

Dove (x;y) sono le coordinate del punto di origine mentre (x';y') sono quelle del punto di destinazione (punto traslato).

I termini $x_v$ e $ y_v $ sono, invece, le componenti del vettore di traslazione del punto $ \vec{v} = \begin{pmatrix} x_v \\ y_v \end{pmatrix} $.

Da queste ricavo le variabili x e y.

$$ \begin{cases} x = x' - x_v  \\ \\ y= y'-y_v \end{cases} $$

Sostituisco x e y nell'equazione della parabola con vertice nell'origine

$$ y = ax^2 $$

$$ y' - y_v = a(x' - x_v)^2 $$

Elimino gli apici alle variabili x' e y' che ho usato solo per distinguerli da quelli della parabola y=ax².

In questo mdoo ottengo l'equazione di una parabola con l'asse parallelo all'asse y e il vertice nel punto $ V (x_v; y_v ) $

$$ y - y_v = a(x - x_v)^2 $$

Svolgo i calcoli algebrici e ricavo y

$$ y  = a \cdot (x^2 - 2xx_v + x_v^2) + y_v $$

$$ y  = ax^2 - 2axx_v + ax_v^2 + y_v $$

Assegno i coefficienti $ b = - 2ax_v $ e $ c =ax_v^2 + y_v $ e ottengo l'equazione della parabola

$$ y  = ax^2 + bx +c  $$

Questo dimostra che ogni equazione parabola con l'asse parallelo all'asse y si può esprimere con l'equazione di secondo grado  $ y  = ax^2 + bx +c  $

Dal coefficiente $ b = - 2ax_v $ ottengo la componente $ x_v $ delle coordinate del vertice

$$ b = - 2ax_v $$

$$ x_v = - \frac{b}{2a} $$

Dal coefficiente $ c =ax_v^2 + y_v $  ottengo la componente $ y_v $ delle coordinate del vertice

$$ c =ax_v^2 + y_v $$

$$ y_v = c - ax_v^2 $$

$$ y_v = c - a (  - \frac{b}{2a} )^2 $$

$$ y_v = c - a (  -1 \cdot \frac{b}{2a} )^2 $$

$$ y_v = c - a (  -1^2 \cdot \frac{b^2}{2^2a^2} ) $$

$$ y_v = c - a (  1 \cdot \frac{b^2}{4a^2} ) $$

$$ \require{cancel} y_v = c - \cancel{a} \cdot \frac{b^2}{4a^\cancel{2}}  $$

$$ y_v = c -  \frac{b^2}{4a}  $$

$$ y_v =  \frac{4ac-b^2}{4a}  $$

Sapendo che il discriminante di un'equazione di secondo grado è $ \Delta = b^2-4ac $ allora $ - \Delta = 4ac - b^2 $

$$ y_v =  \frac{ - \Delta }{4a}  $$

$$ y_v =  - \frac{ \Delta }{4a}  $$

Nota. Per dimostrare che ogni equazione $ y  = ax^2 + bx +c  $ è una parabola, basta traslare l'equazione $ y =ax^2 $ con un vettore spostamento $ \vec{v} = ( x_v ; y_v ) $ $$ y = ax^2 $$ $$ y + y_v = a(x+x_v)^2 $$ Sapendo che  $ x_v = - \frac{b}{2a} $ e  $ y_v =  - \frac{ \Delta }{4a}  $ $$ y  - \frac{ \Delta }{4a} = a(x- \frac{b}{2a})^2 $$ $$ y  = a[x^2-2x\frac{b}{2a}+ (\frac{b}{2a})^2] + \frac{ \Delta }{4a}  $$ $$ y  = ax^2-2ax\frac{b}{2a}+ a \cdot \frac{b^2}{4a^2}  + \frac{ \Delta }{4a}  $$ $$ y  = ax^2-x b+ \frac{b^2}{4a}  + \frac{ \Delta }{4a}  $$ Dove $ \Delta = b^2-4ac $ $$ y  = ax^2-x b+ \frac{b^2}{4a}  + \frac{ b^2-4ac }{4a}  $$ $$ y  = ax^2-x b+ \frac{b^2}{4a}  + \frac{ b^2 }{4a}  - \frac{ 4ac }{4a}  $$ $$ y  = ax^2-x b+ 2 \cdot \frac{b^2}{4a} - c  $$ $$ y  = ax^2-x b+  \frac{b^2}{2a} - c  $$ Quest'ultima è una parabola. Infatti, se considero $ b' = -b $ e $ c' = \frac{b^2}{2a} - c  $ ottengo l'equazione di una parabola in forma standard  $$ y  = ax^2 + b'x + c'  $$ Questo dimostra che la traslazione della parabola $ y = ax^2 $ permette di ottenere qualsiasi parabola parallela all'asse y e quest'ultima è rappresentata da una equazione nella forma $ y=ax^2+bx+c $ .

Equazione della parabola con asse parallelo alle ascisse (x)

L'equazione della parabola con l'asse parallelo all'asse x e il vertice in un punto qualsiasi del piano è la seguente con il coefficiente \( a \ne 0 \) (diverso da zero): $$ x = ay^2 + by + c $$ In alternativa, l'equazione della parabola può essere scritta nella forma generale dove \((h,k)\) è il vertice: $$ x = a (y-k)^2 + h $$ oppure nella forma standard dove \( p \) è la distanza dal fuoco al vertice: $$ (y-k)^2 = 4p(x-h) $$

L'asse di simmetria centrale della parabola è

$$ y = - \frac{b}{2a} $$

L'asse direttrice è

$$ x = - \frac{1+ \Delta}{4a} $$

Dove il discriminante è $ \Delta = b^2-4ac $

Il fuoco della parbola si trova alle coordinate:

$$ F \left( \frac{1- \Delta}{4a}; - \frac{b}{2a} \right) $$

Il vertice si trova alle coordinate

$$ V \left( - \frac{\Delta}{4a}; - \frac{b}{2a} \right) $$

Riassumendo

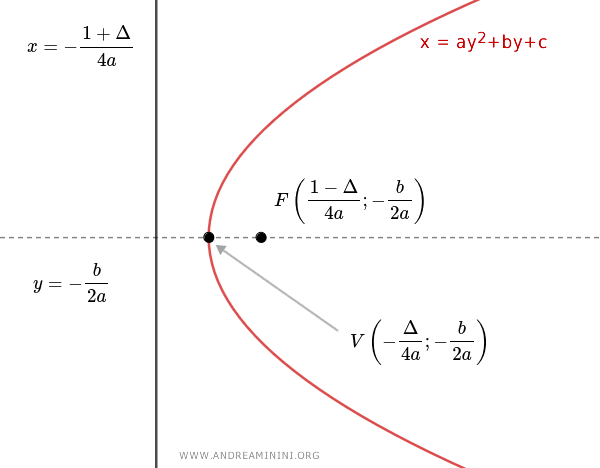
Nota. Anche in questo caso il segno del coefficiente "a" determina la convessità della parabola. Se a>0 la concavita è rivolta verso il semiasse x positivo. Se a<0 è invece rivolta verso il semiasse negativo delle ascisse (x). Inoltre, il valore assoluto del coefficiente "a" determina l'ampiezza della parabola rispetto al suo asse di simmetria.

Esempio

Considero la seguente parabola

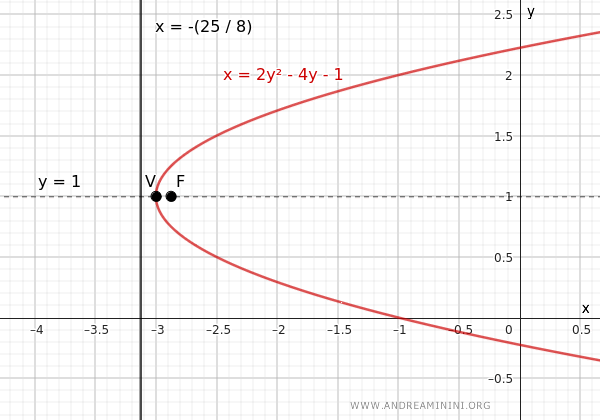
$$ x = 2y^2 - 4y- 1 $$

I coefficienti della parabola sono a=2, b=-4, c=-1 mentre il discriminante è Δ=24.

$$  Δ=b^2- 4ac = (-4)^2-4 \cdot 2 \cdot (-1) = 16+8 = 24 $$

L'asse di simmetria centrale della parabola è il seguente:

$$ y = - \frac{b}{2a} $$

$$ y = - \frac{-4}{2 \cdot 2} $$

$$ y = \frac{4}{4} $$

$$ y = 1 $$

L'asse direttrice della parabola è

$$ x = - \frac{1+ \Delta}{4a} $$

$$ x = - \frac{1+ 24}{4 \cdot 2} $$

$$ x = - \frac{25}{8} $$

Il fuoco della parbola si trova alle coordinate:

$$ F \left( \frac{1- \Delta}{4a}; - \frac{b}{2a} \right) $$

$$ F \left( \frac{1- 24}{4 \cdot 2}; - \frac{-4}{2 \cdot 2} \right) $$

$$ F \left( \frac{- 23}{8}; 1 \right) $$

Il vertice si trova alle coordinate

$$ V \left( - \frac{\Delta}{4a}; - \frac{b}{2a} \right) $$

$$ V \left( - \frac{24}{4 \cdot 2}; - \frac{-4}{2 \cdot 2} \right) $$

$$ V \left( - \frac{24}{8}; - \frac{-4}{4} \right) $$

$$ V \left( - 3; 1 \right) $$

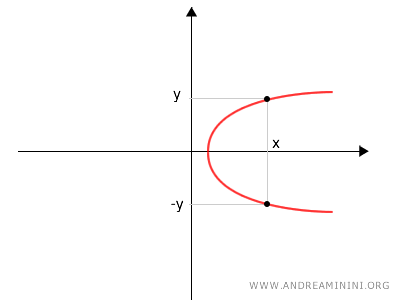
Ecco il grafico della parabola per una conferma visiva.

La dimostrazione

Considero una parabola con l'asse parallelo all'asse y.

$$ y=ax^2+bc+c $$

Per trasformarla in una parabola con l'asse parallelo all'asse x, applico la simmetria assiale rispetto alla bisettrice del I e del II quadrante del piano cartesiano.

$$ \begin{cases} x' = y \\ \\ y' =x \end{cases} $$

Dove x' e y' sono le coordinate dei punti della parabola dopo la trasformazione mentre x e y sono quelli di origine.

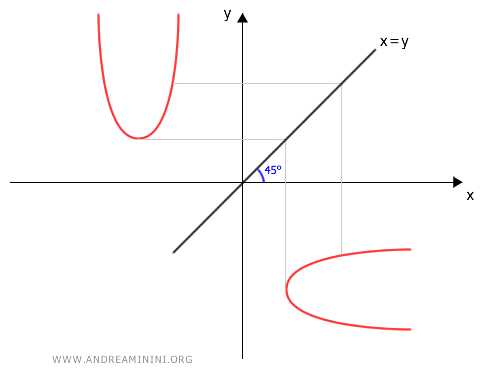
Applico la simmetria all'equazione della parabola con l'asse parallello all'asse y.

$$ y=ax^2+by+c $$

Sostituisco x'=y e y'=x

$$ x'=ay'^2+by'+c $$

Poiché ho usato x' e y' come variabili di comodo per distinguerle dalle coordinate di origine, ora posso anche togliere gli apici.

$$ x=ay^2+by+c $$

Ho così ottenuto l'equazione della parabola con l'asse parallelo all'asse x.

Le formule per calcolare le coordinate del vertice, il fuoco, l'asse direttrice, ecc. si ottengono allo stesso modo. Basta applicare la simmetria assiale rispetto alla bisettrice del primo e del terzo quadrante.

Nota. Da notare che l'equazione $ x=ay^2+by+c $ non è una funzione, perché a ogni valore x non fa corrispondere uno e un solo valore dell'asse y bensì due, fatta eccezione per il vertice della parabola. Quindi, non può essere considerata una funzione da x a y. 

Come determinare l'equazione di una parabola

Per determinare l'equazione di una parabola sono necessarie specifiche informazioni che possono variare a seconda della forma dell'equazione scelta.

In genere, le forme più comuni dell'equazione di una parabola sono:

• Parabola verticale
  L'asse di simmetria della parabola è parallelo all'asse x $$ y = ax^2 + bx + c $$
• Parabola orizzontale
  L'asse di simmetria della parabola è parallelo all'asse x $$ x = ay^2 + by + c $$

In generale, per trovare i valori dei coefficienti a, b, c dell l'equazione di una parabola sono necessari almeno tre parametri distinti o combinazioni specifiche di punti e caratteristiche geometriche (dette "condizioni") come vertice, fuoco e direttrice, ecc.

Ecco alcune condizioni necessarie per determinare completamente l'equazione di una parabola:

• Tre punti distinti
  Conosciendo le coordinate di tre punti distinti attraverso i quali passa la parabola, posso determinare i tre coefficienti \(a\), \(b\) e \(c\) risolvendo un sistema di equazioni lineari.
• Vertice e un altro punto
  Conoscendo le coordinate del vertice (\(h, k\)) e di un altro punto (\(x_1, y_1\)), posso determinare l'equazione della parabola. La forma dell'equazione in questo caso è \(y = a(x-h)^2 + k\). Serve ancora un altro punto per trovare \(a\).
• Asse di simmetria e due punti
  Conoscendo l'asse di simmetria che fornisce il valore \(x = h\) e le coordinate di due punti distinti attraverso i quali passa la parabola, posso determinare l'equazione. L'asse di simmetria fornisce informazioni sul valore di \(b\) se l'equazione è nella forma \(y = ax^2 + bx + c\).
• Direttrice e fuoco
  Conoscendo le coordinate del fuoco (\(h, k + p\)) e la direttrice \(y = k - p\) per una parabola verticale, posso determinare l'equazione della parabola nella forma \( (x - h)^2 = 4p(y - k) \). Analogamente, per una parabola orizzontale, le informazioni sul fuoco e la direttrice determinano l'equazione nella forma \( (y - k)^2 = 4p(x - h) \).

E così via