Equazione del piano

L’equazione del piano è una formula che descrive tutti i punti (x, y, z) che si trovano su un piano nello spazio.  La forma generale dell’equazione di un piano è: $$ ax + by + cz + d = 0 $$ Dove $a, b, c$ sono i coefficienti che rappresentano le componenti di un vettore normale al piano, mentre $d$ è una costante che determina la posizione del piano rispetto all’origine.

È una delle equazioni fondamentali della geometria analitica per rappresentare superfici in tre dimensioni.

Il piano è l’insieme infinito di punti che soddisfano questa equazione generale anche detta forma implicita.

$$ ax + by + cz + d = 0 $$

L'equazione generale del piano può anche essere scritta in forma esplicita, a seconda del problema da risolvere.

$$ z = mx + ny + q $$

Nota. Il vettore normale $\vec{n} = (a, b, c)$ è un vettore perpendicolare al piano, ossia forma un angolo di 90°. In altre parole, ogni direzione nel piano è ortogonale a questo vettore.

Un esempio pratico

Questa equazione rappresenta un piano nello spazio.

$$ 2x - 3y + 4z - 5 = 0 $$

Ogni punto $(x, y, z)$ che risolve questa equazione appartiene al piano.

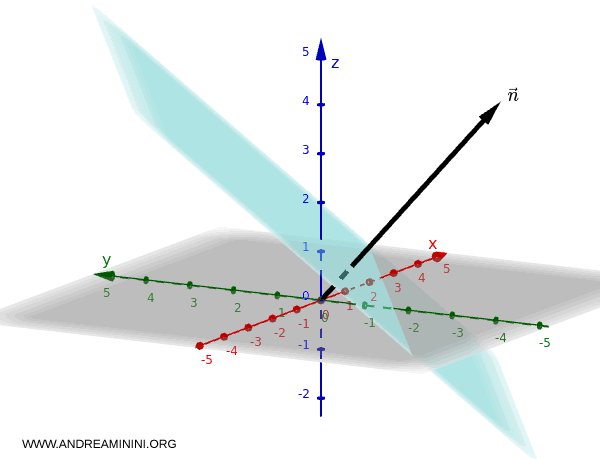
Nel piano $ 2x - 3y +4z - 5 = 0$, il vettore normale è $\vec{n} = (2, -3, 4)$.

Qualsiasi vettore contenuto nel piano sarà perpendicolare a $\vec{n}$.

L'equazione del piano in forma esplicita

L'equazione del piano in forma esplicita si scrive $$ z = m x + n y + q $$

Quando si scrive l’equazione di un piano nello spazio, di solito si usa la forma generale:

$a x + b y + c z + d = 0$

Questa forma è compatta, ma non sempre immediatamente leggibile.

Per renderla più comprensibile, è utile esplicitare la variabile $z$, risolvendo l’equazione rispetto a $z$, a patto che il coefficiente $c \ne 0 $ sia diverso da zero.

$$ c z  = -ax - by - d $$

$$ z = - \frac{a}{c} x - \frac{b}{c} y - \frac{d}{c} $$

Associo ai coefficienti frazionari le lettere $m = -\frac{a}{c}$,  $n = -\frac{b}{c}$,  $q = -\frac{d}{c}$

$$ z = m x + n y + q $$

Questa è detta equazione del piano in forma esplicita.

Quando è possibile scrivere la forma esplicita? È possibile passare alla forma esplicita solo se il piano non è parallelo all’asse $z$. Infatti, se $c = 0$, l’equazione diventa:$$a x + b y + d = 0$$ In questo caso, la variabile $z$ non compare: il piano è parallelo all’asse $z$, e non posso scriverlo nella forma $z = \dots$.

Esempio

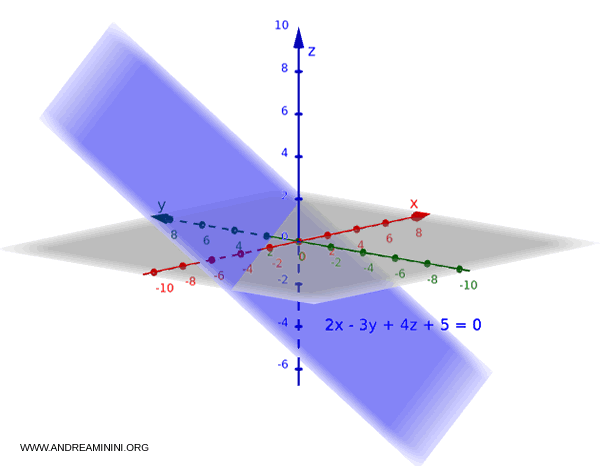
Considero il piano di equazione:

$$ 2x - 3y + 4z + 5 = 0 $$

Poiché $c = 4 \ne 0$, posso scrivere la forma esplicita:

$$ z = -\frac{2}{4}x + \frac{3}{4}y - \frac{5}{4} $$

$$ z = -0.5x + 0.75y - 1.25 $$

In questa forma è facile leggere come varia $z$ al variare di $x$ e $y$, e rappresentare graficamente il piano.

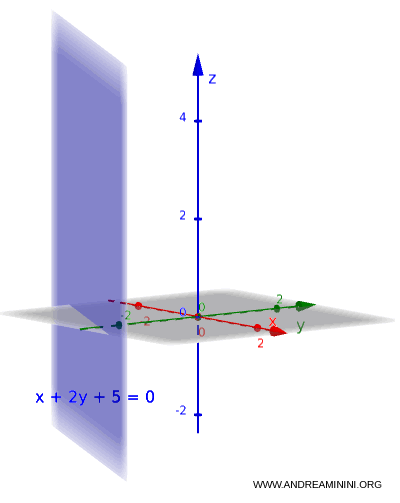
Esempio 2

Prendo invece l’equazione:

$x + 2y + 5 = 0$

Qui $c = 0$, quindi la variabile $z$ non compare. Si tratta di un piano parallelo all’asse $z$, e la forma esplicita non è applicabile.

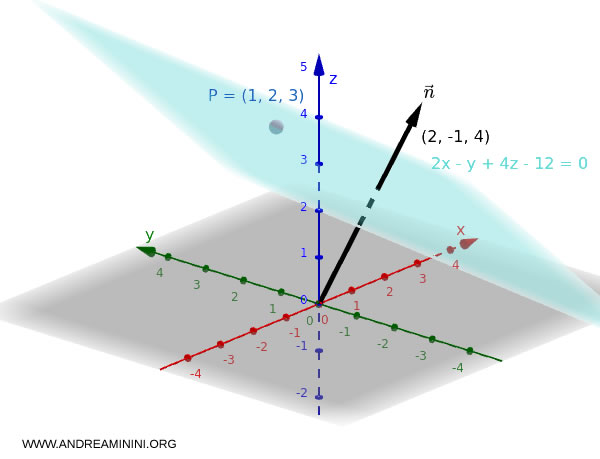
Piano passante per un punto

Se conosco le coordinate di un punto $P_0(x_0, y_0, z_0)$ nello spazio e le componenti di un vettore normale $\vec{n} = (a, b, c)$, posso individuare l’equazione del piano che contiene il punto, usando questa formula: $$ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 $$

Esempio

Considero il punto $P = (1, 2, 3)$ e il vettore normale $\vec{n} = (2, -1, 4)$.

L’equazione del piano passante per $ P_0 $ la ottengo con la formula:

$$ 2(x - 1) - 1(y - 2) + 4(z - 3) = 0 $$

Svolgo i calcoli algebrici.

$$ 2x - 2 - y + 2 + 4z - 12 = 0 $$

$$ 2x - y + 4z - 12 = 0 $$

Questa è l'equazione del piano che passa per $ P = (1, 2, 3) $ ed è perpendicolare al vettore $\vec{n} = (2, -1, 4)$.

La distanza tra un punto e il piano

Data l’equazione del piano $ax + by + cz + d = 0$ e un punto $P(x_1, y_1, z_1)$ nello spazio, la distanza tra il punto e il piano è: $$ \text{Distanza} = \frac{|a x_1 + b y_1 + c z_1 + d|}{\sqrt{a^2 + b^2 + c^2}} $$

Esempio

Devo trovare la distanza dal punto $P = (1,1,1)$ al piano $x + y + z - 3 = 0$:

$$ \text{Distanza} = \frac{|1 + 1 + 1 - 3|}{\sqrt{1^2 + 1^2 + 1^2}} = \frac{0}{\sqrt{3}} = 0 $$

La distanza tra il punto e il piano è zero, questo significa che il punto appartiene al piano.

Piani particolari nello spazio

Alcuni piani nello spazio cartesiano sono particolari, perché l’equazione che li rappresenta coinvolge solo alcune variabili o manca di alcuni coefficienti.

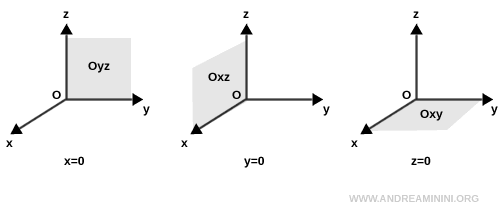
Piani coordinati

Se l’equazione del piano contiene una sola variabile, rappresenta piani paralleli a uno dei piani coordinati.

I tre piani coordinati principali sono:

• Il piano Oyz che si ottiene quando $ x=0 $
• Il piano Oxz che si ottiene quando $ y=0 $
• Il piano Oxy che si ottiene quando $ z=0 $

Questi tre piani sono detti "piani coordinati" perché coincidono con i piani formati da due dei tre assi cartesiani.

Piani paralleli ai piani coordinati

Quando l’equazione è della forma $ x = k $, $ y = k $, oppure $ z = k $, il piano è parallelo a uno dei piani coordinati.

• Se $ x = k $ il piano è parallelo al piano Oyz
• Se $ y = k $ il piano è parallelo al piano Oxz
• Se $ z = k $ il piano è parallelo al piano Oxy

Dove k è un numero reale qualsiasi, costante e diverso da zero $ k \ne 0 $

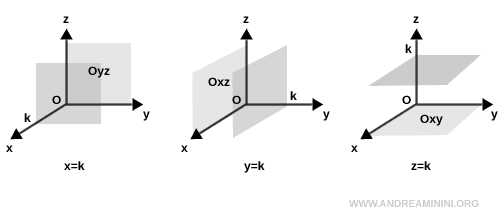
Questi piani hanno la stessa inclinazione dei piani coordinati, ma sono traslati lungo l’asse corrispondente. 

Piani con un coefficiente nullo

Se uno dei coefficienti è nullo, il piano risulta parallelo all’asse corrispondente e perpendicolare al piano individuato dagli altri due assi.

Considero ora l’equazione generale del piano:

$$ ax + by + cz + d = 0 $$

In particolare:

• Se $ c = 0 $, l’equazione diventa $ax + by + d = 0$. Il piano è parallelo all’asse z e perpendicolare al piano Oxy.

  Ad esempio, il piano $ 3x + 4y + 0·z + 5 = 0 $, ossia $ 3x + 4y + 5 = 0 $, è parallelo all’asse z e perpendicolare al piano Oxy.
  

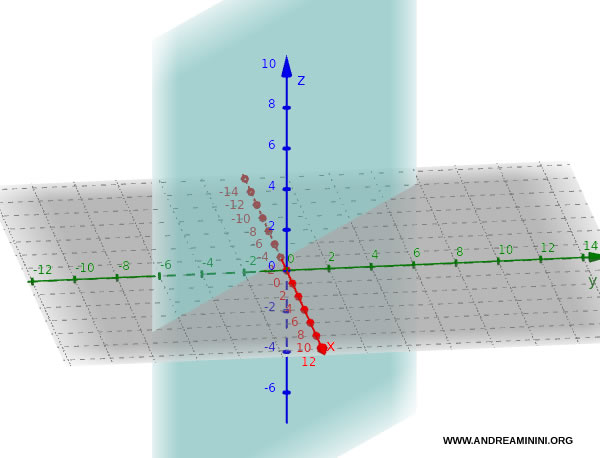
• Se $ b = 0 $, l’equazione diventa $ax + cz + d = 0$. Il piano è parallelo all’asse y e perpendicolare al piano Oxz.

  Ad esempio, il piano $ 3·x + 0 \cdot y + 5z + 5 = 0 $, cioè $ 3x + 5z + 5 = 0 $, è parallelo all’asse y e perpendicolare al piano Oxz.
  

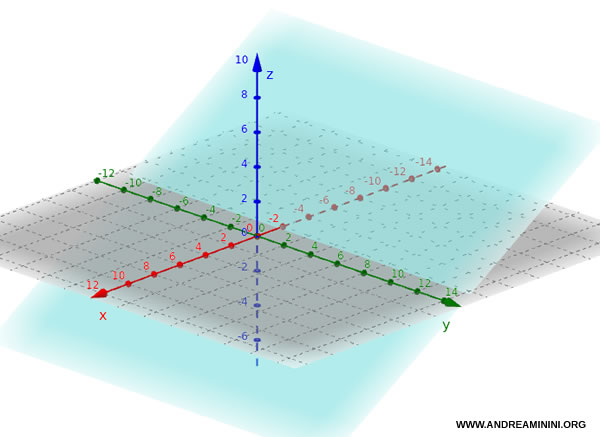
• Se $ a = 0 $, l’equazione diventa $by + cz + d = 0$. Il piano è parallelo all’asse x e perpendicolare al piano Oyz.

  Ad esempio, il piano $ 0·x + 4y + 5z + 5 = 0 $, cioè $ 4y + 5z + 5 = 0 $, è parallelo all’asse x e perpendicolare al piano Oyz.
  

Equazioni parametriche di un piano

Un piano può anche essere descritto con due vettori indipendenti nel piano e un punto di partenza. $$ \vec{r}(s,t) = P_0 + s \cdot \vec{v_1} + t \cdot \vec{v_2} $$ Dove $s, t \in \mathbb{R}$ sono parametri, $ P_0 = (x_0, y_0, z_0) $ è il punto e $ \vec{v_1} $ e $ \vec{v_2}$ sono due vettori nel piano.

Esempio

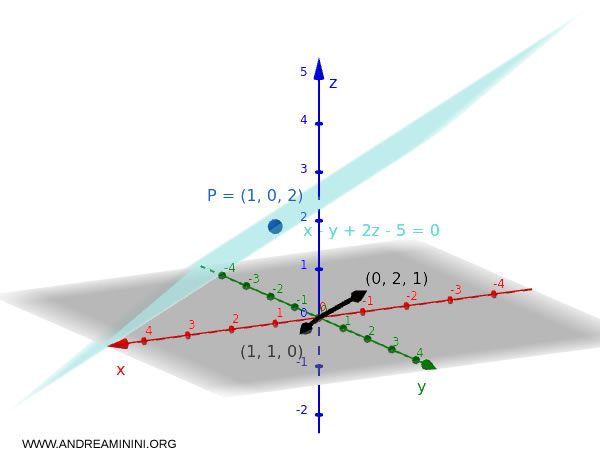
Considero il punto $P_0 = (1,0,2)$ e due vettori $\vec{v_1} = (1,1,0)$, $\vec{v_2} = (0,2,1)$.

Con questi dati, la forma parametrica del piano è:

$$ \vec{r}(s,t) = (1,0,2) + s(1,1,0) + t(0,2,1) $$

Riscrivo l'equazione vettoriale in forma cartesiana

$$ \begin{cases}
x = 1 + s \\
y = s + 2t \\
z = 2 + t
\end{cases}
$$

Questo sistema descrive lo stesso piano, ma in forma esplicita parametrica, dove $ s $ e $ t $ sono parametri liberi. E' un altro modo per rappresentare il piano.

Per ottenere l’equazione cartesiana del piano, elimino i parametri $s$ e $t$.

Ricavo $ s $ dalla prima equazione: $s = x - 1$

$$ \begin{cases}
s = x - 1  \\
y = s + 2t \\
z = 2 + t
\end{cases}
$$

Ricavo $ t $ dalla terza equazione: $t = z - 2$

$$ \begin{cases}
s = x - 1  \\
y = s + 2t \\
t = z-2
\end{cases}
$$

Sostituisco $ s $ e $ t $ nella seconda equazione

$$ \begin{cases}
s = x - 1  \\
y = (x - 1) + 2(z - 2) \Rightarrow y = x + 2z - 5 \\
t = z-2
\end{cases}
$$

Quindi l'equazione del piano è

$$ y = x + 2z - 5 $$

Portando tutto al primo membro ottengo l'equazione cartesiana del piano in forma generale:

$$ x - y + 2z - 5 = 0 $$

Verifica. Controllo se il punto iniziale $P_0 = (1,0,2)$ appartiene al piano. Sostituisco le coordinate del punto ( $x=1 $, $y=0$, $z=2$ nell'equazione del piano $ x - y + 2z - 5 = 0 $ $$ 1 - 0 + 2 \cdot 2 - 5 = 1 + 4 - 5 = 0 $$ L'equazione è soddisfatta, questo significa che il punto appartiene al piano.

La dimostrazione

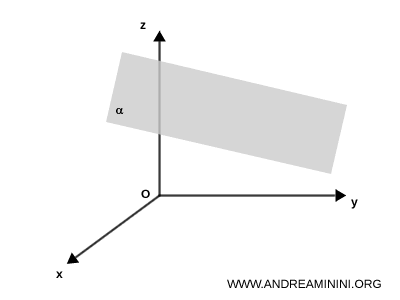
Per dimostrare l'equazione generale del piano, considero un piano $ \alpha $ che non passa per l'origine $ O(0,0,0) $ degli assi cartesiani.

Traccio un vettore perpendicolare al piano $ alpha $ che lo interseca nel punto $ A = (a,b,c) $.

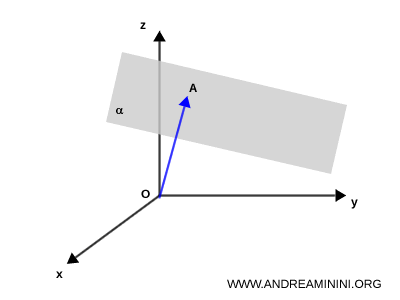
Quindi, il segmento $ OA \perp \alpha $ è perpendicolare al piano $ \alpha $

Ora prendo un punto qualsiasi $ P = (x,y,z) $ sul piano $ \alpha $, diverso da $ A =(a,b,c) $

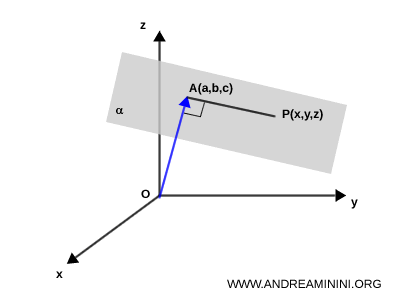
Sapendo che $ OA \perp \alpha $ e $ P \in \alpha $, deduco che anche i segmenti $ AP \perp OA $ sono perpendicolari tra loro.

Infine, traccio il segmento $ OP $.

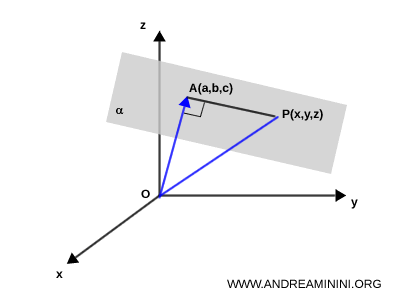
In questo modo ottengo per costruzione un triangolo rettangolo $ OAP $.

Secondo il teorema di Pitagora vale la relazione:

$$ OP^2 = OA^2 + AP^2 $$

Sapendo che la formula della distanza tra due punti nello spazio è:

$$ \text{Distanza}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 $$

La distanza tra i punti $ O(0,0,0) $ e $ A(a,b,c) $ è

$$ OA^2 = (a - 0)^2 + (b -0)^2 + (c -0)^2 = a^2+b^2+c^2 $$

La distanza tra i punti $ O(0,0,0) $ e $ P(x,y,z) $ è

$$ OP^2 = (x - 0)^2 + (y -0)^2 + (z -0)^2 = x^2+y^2+z^2 $$

La distanza tra i punti $ P(x,y,z) $ e $ A(a,b,c) $ è

$$ AP^2 = (x - a)^2 + (y -b)^2 + (z -c)^2  $$

Quindi, la relazione tra i segmenti diventa:

$$ OP^2 = OA^2 + AP^2 $$

$$ ( x^2+y^2+z^2) = (a^2+b^2+c^2) + [(x - a)^2 + (y -b)^2 + (z -c)^2] $$

$$ x^2+y^2+z^2 = a^2+b^2+c^2 + x^2 - 2ax + a^2 + y^2 - 2by +b^2 + z^2 - 2cz + c^2 $$

$$ x^2+y^2+z^2 - a^2 - b^2 - c^2 - x^2 + 2ax - a^2 - y^2 + 2by - b^2 - z^2 + 2cz - c^2 = 0 $$

$$ - 2a^2 - 2b^2 - 2c^2 + 2ax  + 2by + 2cz  = 0 $$

Divido entrambi i membri dell'equazione per 2

$$ (- 2a^2 - 2b^2 - 2c^2 + 2ax  + 2by + 2cz):2  = 0:2 $$

$$ - a^2 - b^2 - c^2 + ax  + by + cz  = 0 $$

$$ ax  + by + cz - (a^2+b^2+c^2)  = 0 $$

Ponendo $ d = - (a^2+b^2+c^2) $ ottengo l'equazione generale del piano.

$$ ax  + by + cz + d  = 0 $$

E così via.