Piani paralleli
Due piani nello spazio sono paralleli se soddisfano una delle seguenti condizioni:
- Non hanno punti in comune, cioè non si intersecano. Questi sono detti piani paralleli non coincidenti.
- Hanno tutti i punti in comune, ovvero coincidono perfettamente. Questi sono detti piani coincidenti.
Ad esempio, i pavimenti di due piani di un edificio, se perfettamente orizzontali, sono piani paralleli non coincidenti.
La distanza tra due piani paralleli
La distanza tra due piani paralleli non coincidenti è la lunghezza del segmento perpendicolare che collega un punto di un piano con un punto dell’altro.
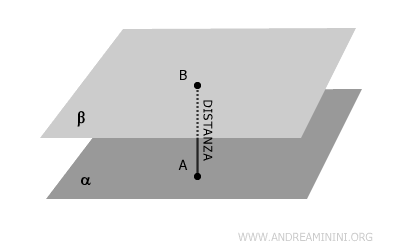
Questa distanza è costante per tutti i punti dei due piani.
Come si calcola la distanza tra due piani
In geometria analitica due piani hanno equazioni del tipo:
$$ Ax + By + Cz + D_1 = 0 $$
$$ Ax + By + Cz + D_2 = 0 $$
La distanza tra i due piani paralleli è data dalla formula seguente:
$$ d = \frac{|D_2 - D_1|}{\sqrt{A^2 + B^2 + C^2}} $$
Dove \( A, B, C \) sono i coefficienti della normale ai piani.
Nota. Ovviamente, se la distanza è nulla $ d=0 $, i due piani sono coincidenti. Se, invece, la distanza è un valore positivo $ d>0 $, i due piani sono paralleli non coincidenti.
Esempio pratico
Considero due piani paralleli con equazioni:
$$ 2x + 3y + 6z + 4 = 0 $$
$$ 2x + 3y + 6z - 8 = 0 $$
Applicando la formula:
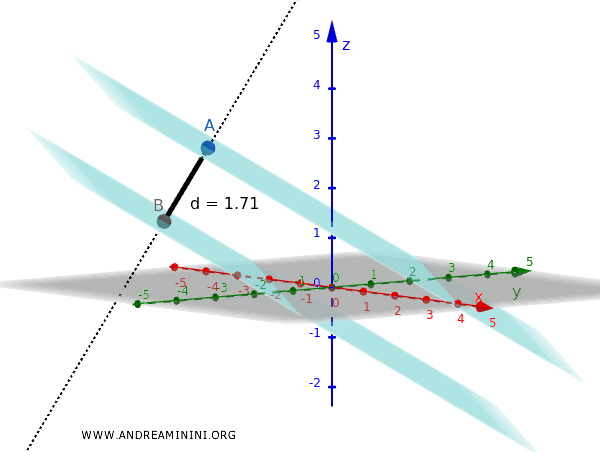
$$ d = \frac{| -8 - 4 |}{\sqrt{2^2 + 3^2 + 6^2}} = \frac{12}{\sqrt{4+9+36}} = \frac{12}{\sqrt{49}} = \frac{12}{7} \approx 1.71 $$
Quindi, la distanza tra i due piani è 1.71 unità.
Proprietà del parallelismo tra piani
Il parallelismo tra piani gode delle seguenti proprietà matematiche:
- Proprietà riflessiva: ogni piano è parallelo a se stesso. $$ \alpha \parallel \alpha $$
- Proprietà simmetrica: se un piano \(\alpha\) è parallelo a un piano \(\beta\), allora anche il piano \(\beta\) è parallelo a \(\alpha\). $$ \alpha \parallel \beta \quad \Rightarrow \quad \beta \parallel \alpha $$
- Proprietà transitiva: se un piano \(\alpha\) è parallelo a un piano \(\beta\) e \(\beta\) è parallelo a un piano \(\gamma\), allora anche \(\alpha\) è parallelo a \(\gamma\). $$ \alpha \parallel \beta, \quad \beta \parallel \gamma \quad \Rightarrow \quad \alpha \parallel \gamma $$
Queste tre proprietà dimostrano che il parallelismo tra piani è una relazione di equivalenza in geometria.
Condizione di parallelismo fra piani
Date le equazioni generali di due piani $$ ax+by+cz+d = 0 $$ $$ a'x+b'y+c'z+d' = 0 $$ i due piani sono paralleli se $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$ In particolare, i due piani sono coincidenti se anche $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} $$
Considero due piani con equazioni generali:
$$ ax + by + cz + d = 0 $$
$$ a'x + b'y + c'z + d' = 0 $$
I coefficienti $ a, b, c $ e $ a', b', c' $ rappresentano le componenti dei vettori normali ai due piani:
$$ \vec{n} = (a, b, c), \quad \vec{n'} = (a', b', c') $$
I due piani sono paralleli se e solo se i vettori normali sono proporzionali, cioè esiste un numero reale \$ k \$ tale che:
$$ \vec{n} = k \, \vec{n'} \quad \text{ovvero} \quad (a, b, c) = k \, (a', b', c') $$
In pratica, si verifica che:
$$
\begin{cases}
a = k a' \\
b = k b' \\
c = k c'
\end{cases}
$$
In altre parole, il rapporto tra i coefficienti delle variabili deve essere lo stesso.
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = k $$
In altre parole, i coefficienti $ a, b, c $ devono essere tutti proporzionali ai corrispondenti $ a', b', c' $.
Attenzione. Se uno o più tra $ a′,b′,c′ $ sono nulli, per la proporzionalità dei vettori normali è necessario che i corrispondenti coefficienti $ a,b,c $ siano anch’essi nulli. In altre parole:
- Se $ a′=0 $ allora deve essere $ a=0 $
- Se $ b′=0 $ allora deve essere $ b=0 $
- Se $ c′=0 $ allora deve essere $ c=0 $
Condizione di coincidenza dei piani
Due piani:
$$ a x + b y + c z + d = 0 $$
$$ a' x + b' y + c' z + d' = 0 $$
sono coincidenti se esiste un numero reale $k \neq 0$ tale che:
$$ (a, b, c, d) = k \cdot (a', b', c', d') $$
In altre parole: l’intero vettore dei coefficienti (incluso il termine noto) deve essere proporzionale.
In pratica, questa condizione può essere verificata osservando che:
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} = k $$
quando i rapporti sono ben definiti, cioè quando tutti i denominatori sono diversi da zero.
Nota. Se uno o più denominatori sono nulli, allora la condizione di coincidenza richiede che i corrispondenti numeratori siano anch’essi nulli, e che i coefficienti restanti rispettino comunque la proporzionalità. Ad esempio, se $ d'=0 $ allora anche $ d=0 $ deve essere nullo, e viceversa.
Esempio
Considero i due piani:
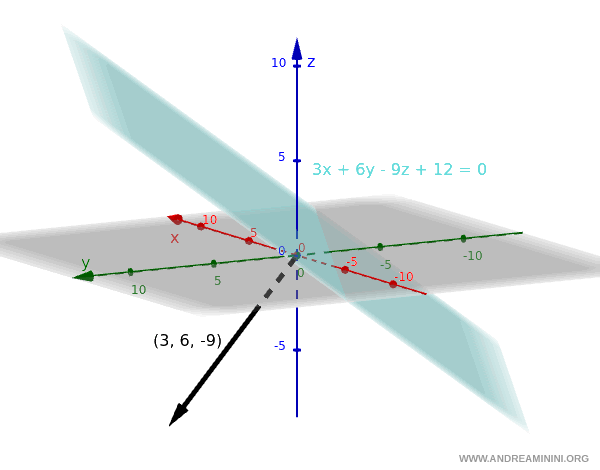
$$ 3x + 6y - 9z + 12 = 0 $$
$$ x + 2y - 3z + 4 = 0 $$
Calcolo i rapporti tra i coefficienti:
$$ \frac{3}{1} = 3, \quad \frac{6}{2} = 3, \quad \frac{-9}{-3} = 3 $$
Quindi, tutti i rapporti tra i coefficienti sono uguali.
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = 3 $$
Questo significa che i vettori normali sono proporzionali e i due piani sono paralleli.
Nota. I coefficienti sono le componenti dei vettori normali ai due piani: $$ \vec{n} = (3,6, -9), \quad \vec{n'} = 1,2, -3) $$ Dove per "normale" si intende un vettore che forma un angolo di 90° con il piano. Ecco un esempio pratico di vettore normale.
Ora controllo anche il termine noto:
$$ \frac{12}{4} = 3 $$
Anche questo rapporto è uguale a 3. Quindi:
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} = 3 $$
Quindi, i due piani non sono soltanto paralleli, ma sono proprio coincidenti.
Note
Alcune note aggiuntive e osservazioni personali sui piani paralleli
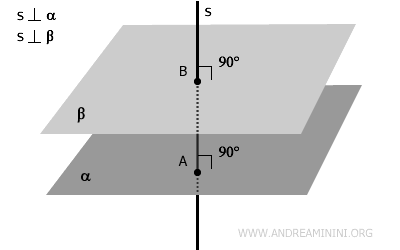
- Se due piani sono paralleli, allora una retta perpendicolare a un piano è perpendicolare anche all'altro piano.
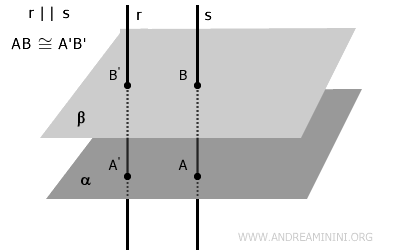
- Dati due piani paralleli e due rette parallele che li intersecano, in modo perpendicolare o meno, i segmenti paralleli che appartengono alle rette e compresi tra i piani sono segmenti congruenti $ AB \cong A'B' $.
E così via.
