Integrazione per sostituzione

Data una funzione continua f(x) e una funzione derivabile g(x) con derivata continua, risulta $$ \int f(x) \: dx = \int f(g(t)) \cdot g'(t) \:dt $$ con x=g(t).

A cosa serve?

L'integrazione per sostituzione è una formula per calcolare gli integrali indefiniti.

Ci sono due possibili metodi di sostituzione

La formula si può usare in un verso oppure nell'altro.

• Primo metodo. Si sostituisce la variabile x con la funzione g(t) e il differenziale dx con g'(t)dt. La funzione f() è la stessa ma cambia il dominio.
  
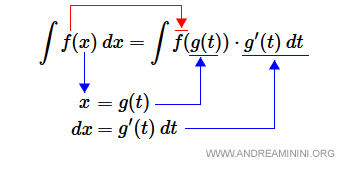
• Secondo metodo. In questo caso la funzione integranda è una funzione composta del tipo f(g(x))·g'(x). Si sostituiscono le funzioni g(x) e g'(x) con la variabile t e il differenziale dt.
  

Quale metodo scegliere? Dipende dalla funzione integranda. A volte conviene il primo metodo, altre volte il secondo. Non c'è una regola generale. L'unica regola è fare molta pratica con gli esercizi.

Un esercizio di esempio

Esempio 1

Devo risolvere l'integrale

$$ \int \frac{ \sin \sqrt{x} }{\sqrt{x}} \: dx $$

Applico il primo metodo dell'integrazione per sostituzione.

L'elemento più ostico dell'integrale è √x.

Per semplificare il calcolo assegno t=√x e ricavo la x e la dx

$$ t = \sqrt{x} $$

$$ x = t^2 $$

$$ dx = D[t^2] \: dt = 2t \: dt $$

Poi applico la formula di integrazione per sostituzione

$$ \int f(x) \: dx = \int f(g(t)) \cdot g'(t) \:dt $$

$$ \int \frac{ \sin \sqrt{x} }{\sqrt{x}} \: dx = \int \frac{ \sin \sqrt{t^2} }{\sqrt{t^2}} \cdot 2t \:dt $$

$$ = \int \frac{ \sin t }{t} \cdot 2t \:dt $$

$$ = \int \sin t \cdot 2 \:dt $$

$$ = 2 \cdot \int \sin t \:dt $$

$$ = 2 \cdot ( - \cos t ) + c $$

$$ = 2 \cdot ( - \cos \sqrt{x} ) + c $$

Esempio 2

Devo risolvere l'integrale

$$ \int \cos x \cdot \sin ( \sin x ) dx $$

In questo caso la funzione integranda è il prodotto tra una funzione cos(x) e una funzione composta sin(sin x).

La funzione cos(x) è la derivata del dominio della funzione composta sin(sin x).

Quindi, mi conviene usare il secondo metodo.

Scelgo di sostituire sin x con t

$$ t = \sin x $$

$$ dt = \cos x \: dx $$

Sostituisco t a sin x e dt a cos x dx

$$ \int \cos x \cdot \sin ( \sin x ) dx $$

$$ \int \sin ( t ) \: dt $$

In questo modo ottengo un integrale più facile da risolvere.

$$ \int \sin ( t ) \: dt = - \cos t + c $$

Sapendo che t=sin x

$$ - \cos t + c $$

$$ - \cos ( \sin x ) + c $$

Quindi, il risultato dell'integrale è

$$ \int \cos x \cdot \sin ( \sin x ) \: dx = - \cos ( \sin x ) + c $$

Esempio 3

Devo risolvere questo integrale

$$ \int \frac{1}{\sqrt(x) - 3} \: dx $$

In questo caso scelgo di applicare il primo metodo dell'integrazione per sostituzione.

Sostituisco la variabile x con la funzione g(t)=t²

$$ x=g(t)=t^2 $$

Poi applico la formula di integrazione per sostituzione

$$ \int f(x) \: dx = \int f(g(t)) \cdot g'(t) \:dt $$

$$ \int \frac{1}{\sqrt(x) - 3} \: dx = \int \frac{1}{\sqrt(t^2) - 3} \cdot D[t^2] \:dt $$

$$ = \int \frac{1}{t - 3} \cdot 2t \:dt $$

$$ = 2 \cdot \int \frac{t}{t - 3} \:dt $$

Aggiungo al numeratore +3 e -3

$$ = 2 \cdot \int \frac{t + 3 - 3}{t - 3} \:dt $$

Poi applico la proprietà lineare per suddividere l'integrale in una somma di integrali

$$ = 2 \cdot [ \int \frac{t - 3}{t - 3} \:dt + \int \frac{3}{t - 3} \:dt ]$$

$$ = 2 \cdot [ \int 1 \:dt + 3 \cdot \int \frac{1}{t - 3} \:dt ]$$

Ora ho due integrali elementari.

Il primo integrale è t perché la primitiva di 1 è t.

$$ = 2 \cdot [ t + 3 \cdot \int \frac{1}{t - 3} \:dt ] + c $$

La primitiva del secondo integrale è il logaritmo del valore assoluto |t-3|.

$$ = 2 \cdot [ t + 3 \cdot \log |t-3| ] + c $$

$$ = 2t + 6 \cdot \log |t-3| + c $$

A questo punto sostituisco la variabile t con la x sapendo che x=t²

$$ t=\sqrt{x} $$

Quindi

$$ = 2t + 6 \cdot \log |t-3| + c $$

$$ = 2 \sqrt{x} + 6 \cdot \log | \sqrt{x} - 3| + c $$

Ho così trovato la soluzione dell'integrale indefinito tramite l'integrazione per sostituzione.

$$ \int \frac{1}{\sqrt(x) - 3} \: dx = 2 \sqrt{x} + 6 \cdot \log | \sqrt{x} - 3| + c $$

Dimostrazione e spiegazione

L'integrazione per sostituzione si basa sulla regola di derivazione delle funzioni composte.

$$ D[F[g(t)] = F'[g(t)] \cdot g'(t) $$

Metto sotto integrale entrambi i membri

$$ \int D[F(g(t)] \: dt = \int F'[g(t)] \cdot g'(t) \: dt $$

L'integrale e la derivata al primo membro dell'equazione si annullano

$$ F(g(t)) = \int F'[g(t)] \cdot g'(t) \:dt $$

Sapendo che F(g(t)) è la primitiva di f(g(t)) allora F'(g(t))=f(g(t))

$$ F(g(t)) = \int f(g(t)) \cdot g'(t) \:dt $$

e F(g(t))=∫f(g(t))dt

$$ \int f(g(t)) \: dt = \int f(g(t)) \cdot g'(t) \:dt $$

Sapendo che x=g(t) modifico il primo membro e diventa

$$ \int f(x) \: dx = \int f(g(t)) \cdot g'(t) \:dt $$

E così via