Teorema della media dell'integrale definito

In una funzione f(x) continua nell'intervallo [a,b] esiste un punto x₀ ∈ [a,b] tale che $$ \int_a^b f(x) \: dx = f(x_0) \cdot (b-a) $$

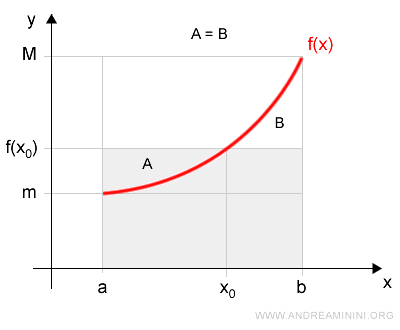
Cosa significa?

L'area individuata dell'espressione f(x₀)·(b-a) è uguale all'area al di sotto della funzione nell'intervallo [a,b], perché le superfici A=B sono uguali.

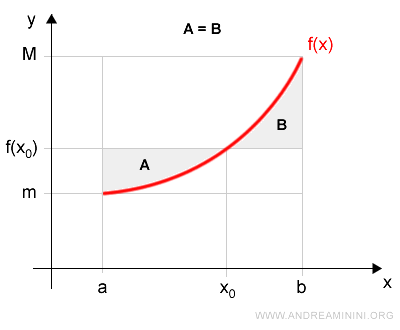
Quindi, conoscendo il valore medio x₀ della funzione nell'intervallo [a,b] posso ottenere lo stesso risultato dell'integrale definito tramite l'espressione f(x₀)·(b-a).

Dimostrazione

Un'integrale definito è un elemento che separa le somme integrali inferiori s(P) dalle somme integrali superiori S(P) per qualsiasi partizione dell'intervallo [a,b].

$$ s(P) \le \int_a^b f(x) \: dx \le S(P) $$

Prendo il caso di una semplice partizione P composta soltanto da due punti [a,b].

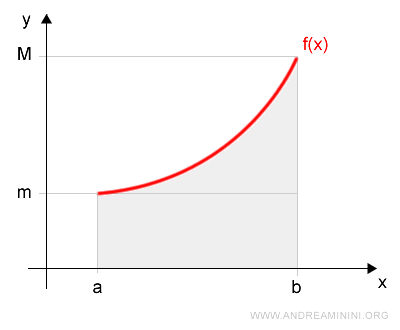
La somma integrale inferiore con m=minimo dell'intervallo chiuso è

$$ s(P) = m \cdot (b-a) $$

mentre la somma integrale superiore con M=massimo dell'intervallo chiuso è

$$ S(P) = M \cdot (b-a) $$

Poi sostituisco le somme s(P) e S(P) nella relazione d'ordine

$$ s(P) \le \int_a^b f(x) \: dx \le S(P) $$

$$ m \cdot (b-a) \le \int_a^b f(x) \: dx \le M \cdot (b-a) $$

Divido tutti i membri per (b-a)

$$ \frac{m \cdot (b-a)}{b-a} \le \frac{\int_a^b f(x) \: dx}{b-a} \le \frac{M \cdot (b-a)}{b-a} $$

$$ m \le \frac{1}{b-a} \cdot \int_a^b f(x) \: dx \le M $$

Pertanto, esiste un punto y₀

$$ y_0 = \frac{1}{b-a} \cdot \int_a^b f(x) \: dx $$

che è intermedio tra m e M

$$ m \le y_0 \le M $$

Quindi, esiste un punto x₀ di [a,b] tale che

$$ y_0 = f(x_0) $$

e questo dimostra il teorema

$$ \frac{1}{b-a} \cdot \int_a^b f(x) \: dx = f(x_0) $$

$$ \int_a^b f(x) \: dx = f(x_0) \cdot (b-a) $$

Nella superficie f(x₀)·(b-a) l'area A è uguale all'area B

Pertanto, l'area individuata dall'espressione f(x₀)·(b-a) è uguale all'integrale ∫f(x) dx nell'intervallo [a,b]

E così via.