L'integrale del prodotto tra funzione composta e derivata

L'integrale indefinito del prodotto tra una funzione composta f(g(x)) e la derivata dell'argomento g(x) è uguale alla primitiva della funzione f(g(x)). $$ \int f(g(x)) \cdot g'(x) \: dx = F(g(x))+k $$

E' l'applicazione inversa della regola di derivazione delle funzioni composte.

Questa regola mi permette di risolvere una vasta famiglia di funzioni integrali.

Un esempio pratico

Devo calcolare l'integrale indefinito

$$ \int 2x \cdot \sin x^2 \: dx $$

Posso considerare la funzione sin x² come una funzione composta f(g(x))

$$ f(g(x)) = \sin x^2 $$

$$ g(x) = x^2 $$

E' subito evidente che 2x è la derivata dell'argomento g(x) della funzione composta f(g(x))

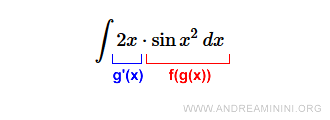
Ora applico la regola di integrazione del prodotto fra funzione composta e derivata.

$$ \int f(g(x)) \cdot g'(x) \: dx = F(g(x))+k $$

$$ \int \sin x^2 \cdot 2x \: dx = F(g(x))+k $$

Nota. La funzione primitiva della funzione composta f(g(x))=sin x² è F(g(x))=-cos x² $$ F(g(x)) = - \cos x^2 $$ Per fare una rapida verifica calcolo la derivata della F(g(x)) con la regola di derivazione delle funzioni composte. $$ D[F(g(x))]=F'(g(x)) \cdot g'(x) $$ $$ D[F(g(x))]=D[- \cos x^2] \cdot D[x^2] $$ $$ D[F(g(x))]= \sin x^2 \cdot 2x $$

Quindi posso scrivere

$$ \int \sin x^2 \cdot 2x \: dx = - \cos x^2 +k $$

Ho così risolto l'integrale

Dimostrazione e spiegazione

Secondo la regola di derivazione di una funzione composta

$$ D[f(g(x))] = f'(g(x)) \cdot g'(x) $$

Per il calcolo integrale

$$ \int h'(x) \: dx = h(x) + k $$

Se considero h'(x) uguale a f'(g(x))

$$ h'(x) = f'(g(x)) = f'(g(x)) \cdot g'(x) $$

Allora ottengo

$$ \int f'(g(x)) \cdot g'(x) \: dx = f(g(x)) + k $$

E così via.