Integrale di linea
L'integrale di linea (o integrale curvilineo) è una quantità scalare ottenuta sommando i prodotti scalari dei vettori v lungo una curva L in un campo vettoriale C. $$ \int_A^B \vec{v} \cdot dl $$
Dove dl è uno spostamento infinitesimale lungo i punti della curva nel tratto compreso tra gli estremi A e B.
Il vettore VP è il vettore tangente alla curva in un determinato punto P della curva.
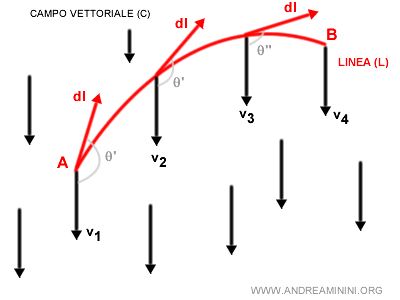
La somma di tutti i prodotti scalari V∧dl è una quantità scalare (un numero) detta integrale di linea o integrale curvilineo.
A cosa serve? In fisica gli integrali di linea sono utili per calcolare il lavoro necessario per spostare un oggetto in un campo di forze.
Un esempio pratico
Prendo in considerazione un campo vettoriale C costante in cui i vettori hanno la stessa intensità, direzione e verso.
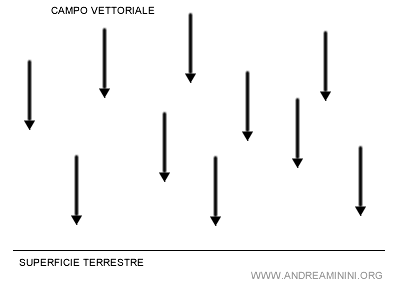
Il campo gravitazionale in un tratto limitato della superficie terrestre è un esempio tipico di campo vettoriale costante.
I vettori indicano la direzione, il verso e l'intensità della forza di gravità (g).
Se volessi lanciare un oggetto dal punto A al punto B con moto rettilineo uniforme dovrei impiegare un lavoro W in grado di compensare la forza di gravità.
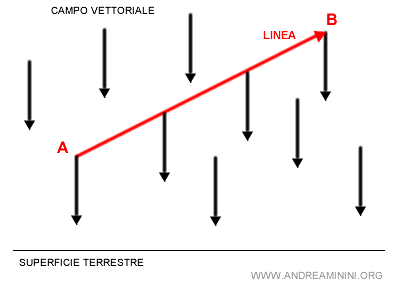
L'integrale di linea mi permette di calcolare il valore scalare della forza F.
Suddivido il tratto da A e B in tratti di lunghezza infinitesima dl.
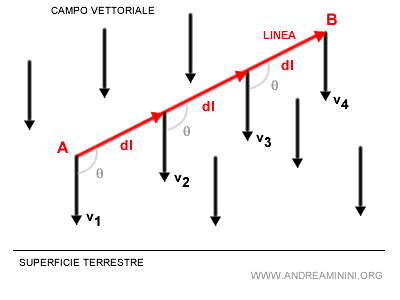
Nota. In questo caso la curva L è una retta. Quindi, i vettori tangenti dl coincidono tutti con la direzione e il verso della retta. $$ W = F·dl $$
Per ogni punto P calcolo il prodotto scalare tra il vettore tangente alla retta e il vettore del campo gravitazionale che hanno origine nel punto P.
$$ \vec{v_1} \cdot d_l = |v_1| \cdot |dl| \cdot \cos \ θ $$
$$ \vec{v_2} \cdot d_l = |v_2| \cdot |dl| \cdot \cos \ θ $$
$$ \vec{v_3} \cdot d_l = |v_3| \cdot |dl| \cdot \cos \ θ $$
La somma di tutti i prodotti scalari è l'integrale di linea, ossia il lavoro W necessario per spostare l'oggetto lungo la linea da A a B.
$$ \int_A^B \vec{v} \ dl = \sum_p \vec{v}_p \cdot dl $$
Esempio 2
Il ragionamento è lo stesso se il campo vettoriale non è costante.
Ad esempio, la forza gravitazionale si riduce man mano che ci si allontana dalla Terra.
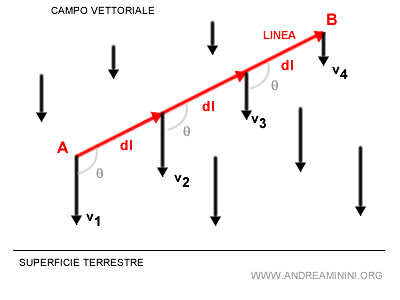
In questo caso i vettori hanno un'intensità (modulo o lunghezza) minore al crescere dell'altitudine.
Quindi, il prodotto scalare è diverso.
Esempio 3
Quando lo spostamento non è rettilineo, la traiettoria è una curva.
In questo caso devo calcolare in ogni punto il vettore tangente dl alla curva.
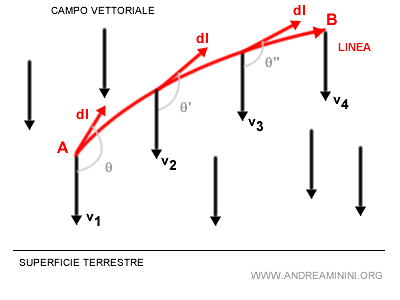
Ora vettori tangenti hanno direzione, intensità e verso variabili.
L'ampiezza dell'angolo θ tra il vettore tangente e il vettore del campo vettoriale cambia in ogni punto della curva.
Di conseguenza cambia anche il prodotto scalare.
Nota. In alternativa, per ottenere un valore approssimato posso anche calcolare il prodotto scalare usando il vettore della spezzata tra coppie di punti della curva anziché il vettore tangente in ogni punto della curva.
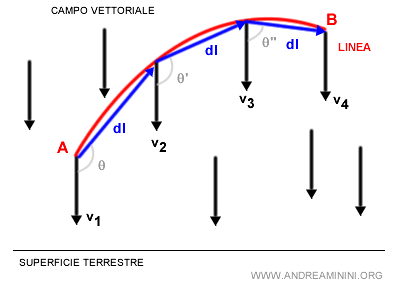
Ogni prodotto scalare misura un lavoro parziale (o lavoro elementare). La somma di tutti i lavori parziali è un'approssimazione del lavoro necessario per spostare l'oggetto. Quanto più piccolo è l'intervallo dl della spezzata, tanto minore è l'errore di approssimazione dell'integrale curvilineo.
Esempio 4
Lo stesso ragionamento posso applicarlo a campi vettoriali più complessi.
Ad esempio, se lo spostamento avviene in uno spazio con correnti d'aria o d'acqua diverse.
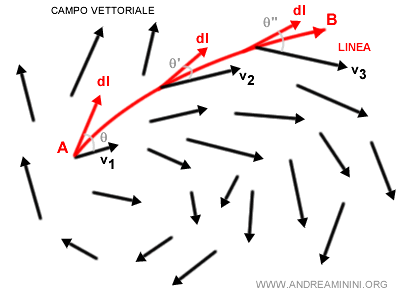
Il prodotto scalare cambia in ogni punto lungo la curva.
Le proprietà degli integrali curvilinei
Gli integrali curvilinei hanno le stesse proprietà degli integrali definiti.
- Preso un punto intermedio C nell'intervallo [A,B], la somma degli integrali curvilinei dei due archi [A,C] e [C,B] è uguale all'integrale curvilineo tra gli estremi A e B (additività). $$ \int_A^B \vec{v} \ \cdot dl = \int_A^C \vec{v} \ \cdot dl + \int_C^B \vec{v} \cdot \ dl $$
- Percorrendo l'intervallo in senso opposto, l'integrale curvilineo [B,A] è una quantità scalare di segno opposto rispetto all'integrale curvilineo [A,B] $$ \int_A^B \vec{v} \ \cdot dl = - \int_B^A \vec{v} \cdot \ dl $$
La circuitazione
Si parla di circuitazione (o circolazione) quando gli estremi della curva L sono uguali A=B ossia la curva è chiusa. $$ \oint_{L} \vec{v} \cdot dl $$
In questo caso l'estremo iniziale e finale della curva L coincidono.
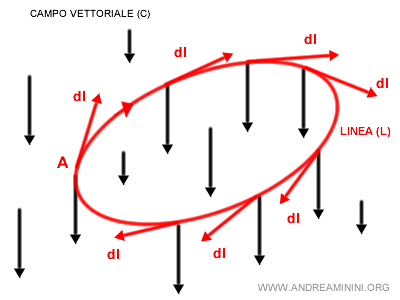
Per indicare l'integrale curvilineo di una circuitazione si usa un simbolo diverso ∮.
$$ \oint_{L} \vec{v} \cdot dl = \int_A^A \vec{v} \cdot dl $$
Cambiando il verso di percorrenza lungo la circuitazione L, l'integrale curvilineo cambia di segno.
E così via.
