Integrale triplo
L’integrale triplo di una funzione di tre variabili \( f(x, y, z) \) definita su una regione solida \( E \subseteq \mathbb{R}^3 \) è un’estensione dell’integrale doppio al caso tridimensionale, e si scrive: \[\iiint_E f(x, y, z)\, dV\] Dove \( dV \) rappresenta un elemento infinitesimo di volume (ad esempio \( dx\,dy\,dz \)) ed \( E \) è una regione tridimensionale nello spazio
L'interpretazione geometrica e fisica di un integrale triplo è inizialmente difficile da immaginare.
In parole semplici, se \( f(x, y, z) \geq 0 \), l’integrale triplo rappresenta la quantità totale positiva (come massa, energia o carica) distribuita nello spazio secondo la densità della funzione \( f \)
$$ \iiint_E f(x, y, z)\, dV $$
Quando \( f(x, y, z) \) è in parte positiva e in parte negativa, invece, l'integrale triplo rappresenta una differenza algebrica.
$$ \iiint_E f(x, y, z)\, dV = \text{contributo positivo} - \text{contributo negativo} $$
Ad esempio, se immagino \( f(x, y, z) \) come una densità, allora \( f > 0 \): “riempie” lo spazio (massa positiva) mentre\( f < 0 \) “svuota” lo spazio (massa negativa, oppure deficit, mancanza). Quindi, l’integrale misura il bilancio netto (o differenza algebrica) tra ciò che è “presente” e ciò che è “assente”. In fisica o in ingegneria, una funzione \( f(x, y, z) \) che cambia segno può rappresentare flussi in entrata e uscita.
Come si calcola?
L’integrale triplo posso calcolarlo come un integrale iterato, scegliendo un ordine adatto di integrazione:
\[ \iiint_E f(x, y, z)\, dV = \int_{x_0}^{x_1} \int_{y_0(x)}^{y_1(x)} \int_{z_0(x,y)}^{z_1(x,y)} f(x, y, z)\, dz\,dy\,dx \]
Oppure in altro ordine, a seconda della forma di \( E \).
Cambiare l’ordine di integrazione delle variabili non cambia il valore dell’integrale, ma bisogna fare attenzione a ridisegnare i limiti di integrazione.
Un esempio pratico
Considero l’integrale triplo della funzione \[ f(x, y, z) = z \] nello spazio di integrazione \[ E = [0,1] \times [0,1] \times [0,1] \]
In questo la funzione \( f(x, y, z) = z \) rappresenta una densità che aumenta con l’altezza (z).
L'integrale triplo misura la quantità totale (ad esempio massa) distribuita nel cubo con densità variabile in base a \( z \).
Scrivo l’integrale come iterato:
\[ \iiint_E z\, dV = \int_0^1 \int_0^1 \int_0^1 z\, dz\,dy\,dx \]
Integro rispetto alla variabile \( z \):
\[ \int_0^1 z\, dz = \left[ \frac{z^2}{2} \right]_0^1 = \frac{1}{2} \]
Poi rispetto alla variabile \( y \):
\[ \int_0^1 \frac{1}{2}\, dy = \frac{1}{2} \]
Infine, rispetto alla variabile \( x \):
\[ \int_0^1 \frac{1}{2}\, dx = \frac{1}{2} \]
Il risultato finale è
\[ \iiint_E z\, dV = \frac{1}{2} \]
In questo esempio ho calcolato la massa totale in un cubo dove la densità è nulla alla base (z = 0) e massima in alto (z = 1).
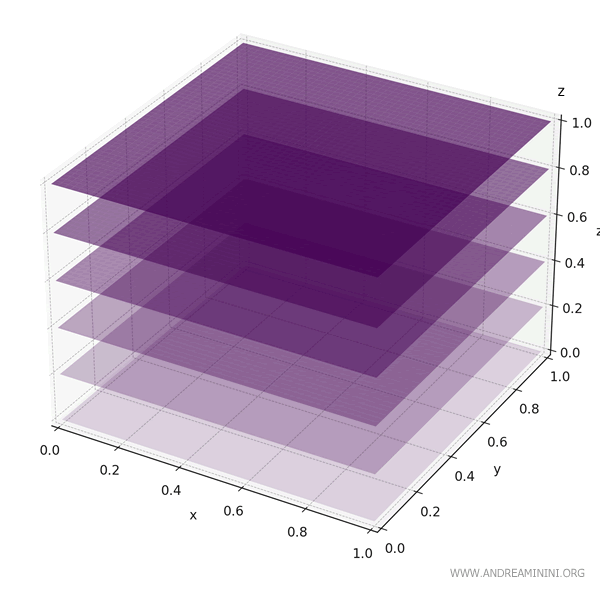
La media dei valori di \( z \) sul cubo è \( \frac{1}{2} \), quindi l’integrale restituisce quella media moltiplicata per il volume \( 1 \cdot 1 \cdot 1 = 1 \).
Esempio 2
Considero la funzione \( f(x, y, z) = z - 0.5 \) nel cubo \( E = [0,1]^3 \) per \( z < 0.5 \), \( f < 0 \) e per \( z > 0.5 \), \( f > 0 \)
Scrivo l’integrale triplo
\[ \iiint_E (z - 0.5)\, dV = \int_0^1 \int_0^1 \int_0^1 (z - 0.5)\, dz\,dy\,dx \]
Integro rispetto a \( z \)
\[ \int_0^1 (z - 0.5)\, dz = \left[ \frac{z^2}{2} - 0.5z \right]_0^1 = \left( \frac{1}{2} - 0.5 \right) = 0 \]
Gli altri due integrali sono sempre nulli.
\[ \int_0^1 \int_0^1 0\, dy\,dx = 0 \]
Quindi, l'integrale triplo è nullo
\[ \iiint_E (z - 0.5)\, dV = 0 \]
Questo accade perché la funzione \( f(z) = z - 0.5 \) è negativa sotto \( z = 0.5 \) e positiva sopra. Quindi, è simmetrica rispetto a \( z = 0.5 \)
Il contributo positivo e quello negativo si compensano perfettamente tra loro.
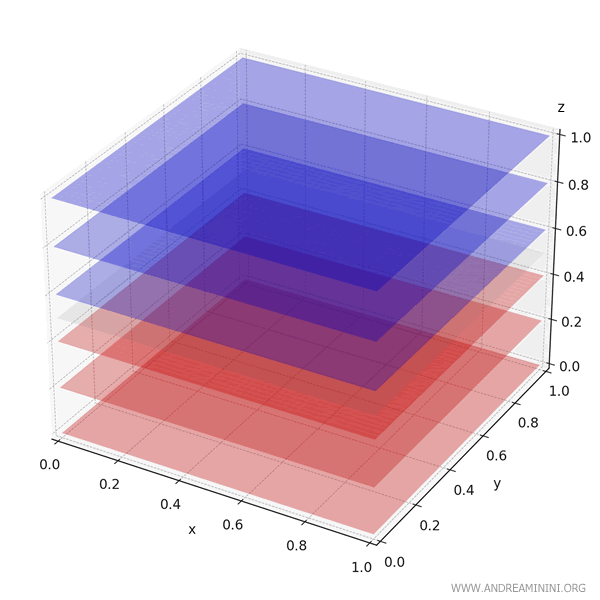
In questo grafico 3D di \( f(x, y, z) = z - 0.5 \) su \( [0,1]^3 \) ho rappresentato:
- Gli strati blu rappresentano le sezioni dove la funzione è positiva: sopra il piano \( z = 0.5 \)
- Gli strati rossi rappresentano le sezioni dove la funzione è negativa sotto il piano \( z = 0.5 \)
Poiché la funzione è simmetrica rispetto al piano \( z = 0.5 \), le due parti (positiva e negativa) si compensano perfettamente, ecco perché l’integrale triplo dà zero.
Nota. Da un punto di vista fisico potrebbero essere delle forze in direzioni opposte (positivo = spinta, negativo = attrazione) che si compensano e si annullano reciprocamente.
E così via.
