Le funzioni primitive
Cos'è una funzione primitiva
Una funzione F(x) è una primitiva della funzione f(x) se F(x) è derivabile nell'intervallo [a,b] e la derivata F'(x)=f(x) per ogni x nell'intervallo [a,b]. $$ F'(x)=f(x) \:\:\: \forall x \in [a,b] $$
Un esempio pratico
Questa funzione
$$ F(x)=x^2 $$
è una primitiva della funzione f(x)=2x
$$ f(x)=2x $$
perché la derivata F'(x) è uguale a f(x)
$$ F(x)= D [ x^2 ] = 2x $$
Da questa osservazione deriva il teorema fondamentale del calcolo integrale.
Se una funzione f(x) è una funzione continua nell'intervallo [a,b], allora la funzione integrale F(x) è una primitiva di f(x) se la derivata di F(x) è uguale a f(x) $$ F(x) = \int_a^b f(x) \: dx $$ con $$ f(x)=F'(x) $$
In realtà, per ogni funzione continua f(x) non esiste soltanto una primitiva F(x) ma una famiglia con infinite primitive nella forma F(x)+k.
La famiglia di primitive
La famiglia di primitive di una funzione f(x) è un insieme composto da funzioni F(x)+k dove k è una costante.
$$ F(x)+k $$
perché la derivata di una costante è sempre zero.
$$ D[F(x)+k] = D[f(x)] + D[k] = D[f(x)] + 0 $$
Esempio. La derivata di F(x)=x2+3 e G(x)=x2+5 è sempre uguale a 2x. $$ F'(x)=D[x^2+3]=2x \\ G'(x)=D[x^2+5]=2x $$ per questa ragione l'integrale di 2x è x2+k $$ \int 2x \: dx = x^2 + k $$ in questo modo si considerano sia la primitiva F(x) che G(x) e tutte le altre infinite primitive della funzione f(x)=2x.
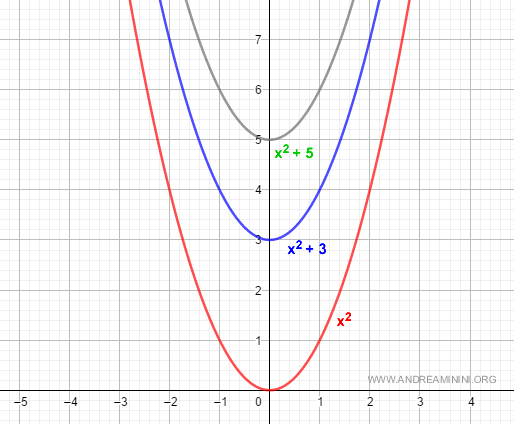
Quindi, l'integrale della funzione f(x) è una famiglia di primitive caratterizzate dalla primitiva F(x) e da una costante k qualsiasi
$$ F(x) = \int_a^b f(x) \: dx $$ con $$ f(x)=F'(x)+k $$
Detto in altri termini
Date due funzioni primitive F(x) e G(x) di una stessa funzione continua f(x) nell'intervallo [a,b], esiste una costante k tale che per ogni x∈[a,b] la funzione G(x) è uguale a F(x)+k $$ G(x)=F(x)+k $$
Dimostrazione
Considero la funzione H(x) pari alla differenza delle primitive G(x)-F(x)
$$ H(x) = G(x)-F(x) $$
Esempio. Date due primitive di f(x)=2x $$ F(x)=x^2+3 \\ G(x) = x^2+5 $$ La funzione H(x) è $$ H(x) = G(x)-F(x) = (x^2+3) - (x^2+5) $$
La derivata della funzione H(x) è nulla
$$ H'(x) = G'(x)-F'(x) $$
Essendo le derivate G'(x)=f(x) e F'(x)=f(x), la differenza G'(x)-F'(x) è nulla.
$$ H'(x) = f(x)-f(x) = 0 $$
Esempio. $$ D[H(x)] = D[G(x)] - D[F(x)] = D[x^2+3] - D[x^2+5] = 2x - 2x = 0 $$
Secondo il teorema di Lagrange nell'intervallo [a,x] dove x∈ [a,b] esiste un valore x0 ∈ [a,x] tale che
$$ H(x)-H(a) = H'(x_0) \cdot (x-a) $$
poiché la derivata H'(x) è nulla nell'intervallo [a,b] anche la differenza H(x)-H(a) è nulla.
$$ H(x)-H(a) = 0 \cdot (x-a) $$
$$ H(x)-H(a) = 0 $$
Pertanto, in ogni x di (a,b] la H(x) è un valore costante pari a H(a).
$$ H(x) = H(a) $$
Quindi, la funzione primitiva G(x) può essere scritta nella forma
$$ H(x) = G(x)-F(x) $$
$$ G(x) = F(x) + H(x) $$
dove H(x) una costante k
$$ G(x) = F(x) + k $$
Le primitive di una funzione sono funzioni continue
Se \( F(x) \) è una primitiva di una funzione \( f(x) \) continua in un intervallo (a,b), allora \( F(x) \) è continua su quell'intervallo.
Questo segue dal Teorema Fondamentale del Calcolo.
Se \( f(x) \) è continua su un intervallo, allora deve esistere una funzione \( F(x) \) tale che la sua derivata sia \( F'(x) = f(x) \).
Dato che \( f(x) \) è continua ed è ottenuta derivando la sua primitiva \( F(x) \), deduco che anche \( F(x) \) deve essere per forza continua.
Esempio
Considero la funzione
$$ f(x) = x^2 $$
Questa funzione è definita e continua sull'intervallo \((-1, 1)\).
La primitiva di \( f(x) = x^2 \) è:
$$ F(x) = \frac{x^3}{3} + C $$
Dove \( C \) è una costante arbitraria.
In questo caso, poiché \( f(x) = x^2 \) è continua su tutto l'intervallo \((-1, 1)\), anche la sua primitiva \( F(x) \) risulta continua su \((-1, 1)\).
Questo esempio mostra che, quando la funzione di partenza è continua su un intervallo, anche la sua primitiva è continua sullo stesso intervallo.
Nota. Se \( f(x) \) non è continua in \((a, b)\), allora il discorso cambia, e parecchio. Non è detto che ci sia una primitiva \( F(x) \) su tutto l’intervallo. La sua primitiva \( F(x) \) può essere anch'essa discontinua nello stesso punto oppure può essere continua. Ecco due esempi pratici:
- Primo caso: la funzione \( f(x) = \frac{1}{x} \) ha una discontinuità in \( x=0 \), e la sua primitiva \( F(x) = \ln |x| + C \) risulta anch'essa indefinita in \( x=0 \). Qui, la discontinuità della primitiva riflette quella di \( f(x) \).
- Secondo caso: la funzione \( f(x) = \frac{1}{\sqrt{|x|}} \) è discontinua (indefinita) in \( x=0 \), ma la sua primitiva \( F(x) = 2 \sqrt{|x|} \) è continua in \( x=0 \), dimostrando che una primitiva può essere continua anche se la funzione di partenza non lo è.
Questi esempi chiariscono bene come il comportamento della primitiva dipenda dalle caratteristiche della funzione integranda, senza dover necessariamente riflettere tutte le sue discontinuità.
E così via.
