Integrale definito
L'integrale definito di una funzione continua f(x) in un intervallo [a,b] si calcola con la seguente formula $$ \int_a^b f(x) \:\:dx = F(b) - F(a) $$ detta formula fondamentale del calcolo integrale.
I numeri a e b sono detti estremi di integrazione.
La funzione f(x) dentro l'integrale è detta funzione integranda.
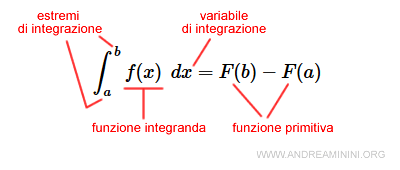
La variabile x (dx) è detta variabile di integrazione.
Nota. La funzione F(x) è la primitiva della f(x) ossia una funzione la cui derivata prima è uguale alla f(x). $$ D[F(x)+k] = f(x) $$ Ad esempio, la funzione f(x)=2x ha come funzione primitiva F(x)=x2+k perché la derivata prima della F'(x)=2x. Dove k è una costante qualsiasi che scompare con la derivata prima in quanto D[k]=0.
Cos'è l'integrale definito di Riemann
Per spiegare l'integrale definito prendo in considerazione una funzione f(x) limitata in un intervallo chiuso [a,b] di R.
![la funzione continua nell'intervallo chiuso [a,b]](http://www.andreaminini.org/data/andreamininiorg/spiegazione-integrale-definito.gif)
Suddivido l'intervallo [a,b] in una partizione P di n+1 punti
$$ x_0, x_1, x_2, ... , x_n $$
dove x0 è l'estremo a e xn è l'estremo b dell'intervallo.
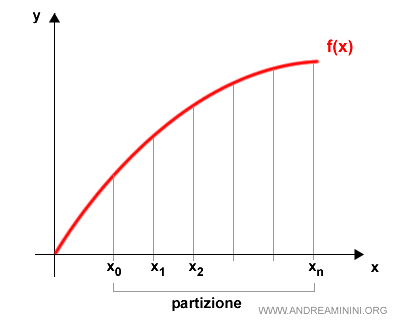
La partizione P individua n intervalli
$$ [x_{k-1}, x_k] \:\:\: con \:\: k=1,...,n $$
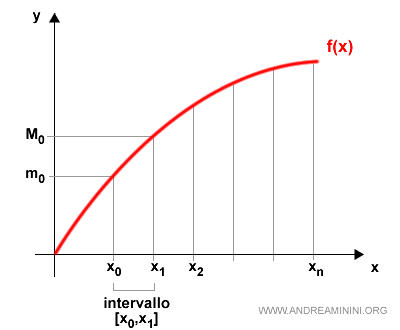
A ogni intervallo è associato un valore minimo e massimo.
$$ m_k = inf[f(x): x \in [x_{k-1}, x_k] ] $$
$$ M_k = sup[f(x): x \in [x_{k-1}, x_k] ] $$
Ad esempio, il primo intervallo [x0,x1] ha un valore minimo m0 e un valore massimo M0.
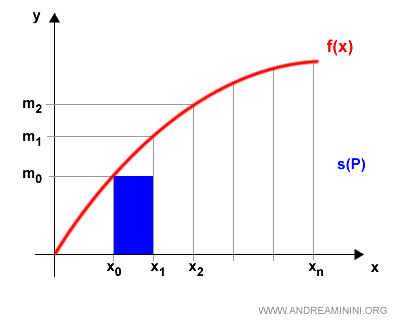
Ogni valore minimo mk moltiplicato per l'intervallo [xk-1,xk] determina l'area di un poligono regolare iscritto nel grafico della funzione.
$$ m_k \cdot (x_k - x_{k-1} ) $$
Ad esempio, nel primo intervallo si ottiene un rettangolo di altezza m0 e base [x0,x1].
Lo stesso accade con i valori massimi Mk.
$$ M_k \cdot (x_k - x_{k-1} ) $$
Ad esempio, nel primo intervallo si ottiene un rettangolo di altezza M0 e base [x0,x1].
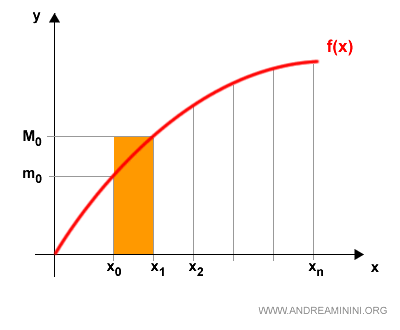
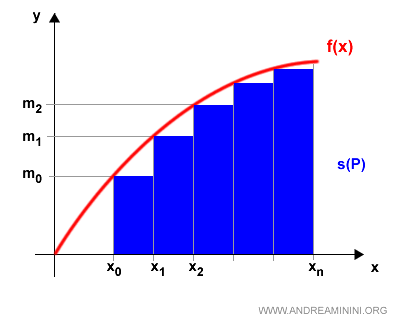
La somma delle aree dei poligoni iscritti è detta somma integrale inferiore.
$$ s(P) = \sum_{k=1}^{n} m_k \cdot (x_k - x_{k-1} ) $$
Ecco la rappresentazione grafica
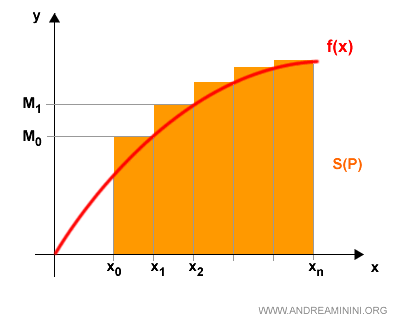
La somma delle aree dei poligoni circoscritti è detta somma integrale superiore.
$$ S(P) = \sum_{k=1}^{n} M_k \cdot (x_k - x_{k-1} ) $$
Ecco la rappresentazione grafica
Il minimo mk è sempre minore o uguale al massimo Mk
$$ m_k \le M_k $$
Pertanto, la somma inferiore s(P) è sempre minore o uguale alla somma superiore S(P).
$$ s(P) \le S(P) $$
Dal punto di vista geometrico la somma integrale superiore eccede quella inferiore
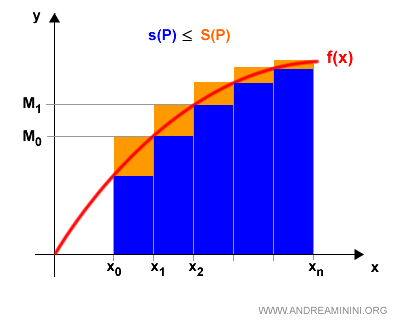
E' facile intuire che l'area tra la funzione f(x) e l'asse delle ascisse è compresa tra s(P) e S(P).
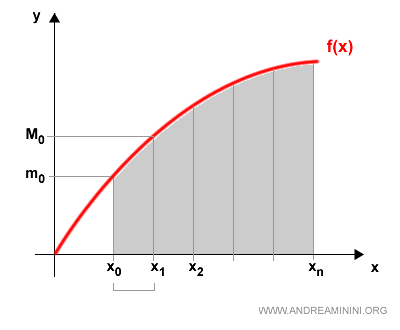
Se cambiassi la partizione P con un'altra partizione Q otterrei una diversa somma integrale inferiore e superiore.
$$ s(Q) \\ S(Q) $$
La partizione Q ha più intervalli.
Pertanto, la differenza tra la somma integrale superiore e inferiore è più piccola rispetto alle precedenti.
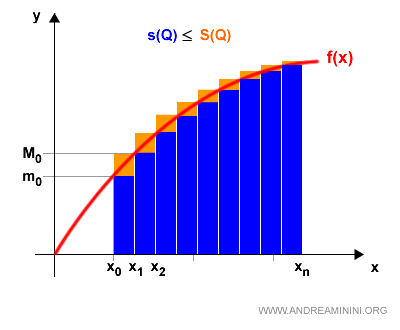
Nota. Dal punto di vista grafico la differenza S(Q)-s(Q) della partizione Q è l'area arancione che eccede quella blu. Come si può vedere, l'area arancione è nettamente inferiore rispetto alla differenza S(P)-s(P) della precedente partizione P. Ovviamente, oltre alla partizione P e Q posso creare infinite altre partizioni. Quanto più intervalli ha una partizione, tanto più la differenza tra la somma integrale superiore e inferiore si riduce.
A questo punto, assegno all'insieme A le somme integrali inferiori di ogni partizione ( es. P, Q, ecc. ).
$$ A = \{s(P), s(Q) \} $$
All'insieme B assegno, invece, le somme integrali superiori di ogni partizione ( es. P, Q, ecc. ).
$$ B = \{S(P), S(Q) \} $$
Gli insiemi A e B sono separati tra loro.
Se tra i due insiemi A e B esiste un elemento unico c che li separa, si dice che la funzione f(x) è integrabile in [a,b] secondo Riemann. $$ c = \sup{A} = \inf{B} $$ L'elemento c è detto integrale definito di f(x) in [a,b] e si indica con il simbolo seguente: $$ \int_a^b f(x) \:\: dx $$
Un esempio pratico
Ho la funzione
$$ f(x)=3x^2 $$
Ecco la rappresentazione grafica
![l'area del grafico nell'intervallo [2,6]](http://www.andreaminini.org/data/andreamininiorg/integrale-funzione-derivata.gif)
Per calcolare l'area tra gli estremi 2 e 6 calcolo l'integrale definito
$$ \int_2^6 3x^2 \: dx $$
Suddivido l'intervallo in una partizione P con due intervalli.
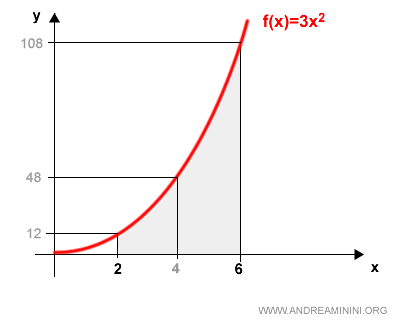
La partizione mi permette di ottenere due rettangoli inscritti e due rettangoli circoscritti.
Ecco i rettangoli inscritti.
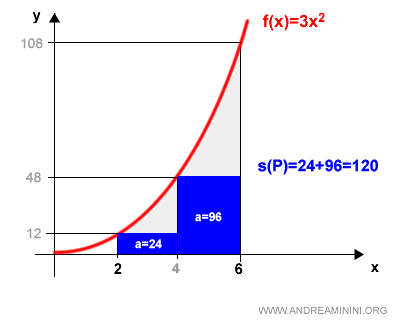
Il primo rettangolo inscritto ha un'area di 24 mentre il secondo di 96.
Pertanto la somma integrale inferiore della partizione P è
$$ s(P)=96+24 = 120 $$
Passo ad analizzare i due rettangoli circoscritti della partizione.
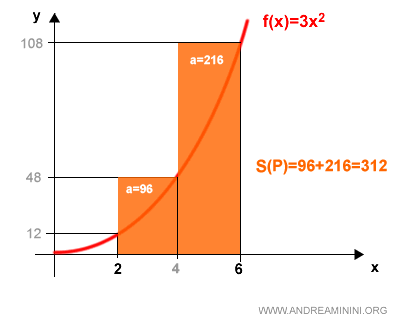
Il primo rettangolo circoscritto ha un'area di 96 mentre il secondo di 216.
Pertanto la somma integrale superiore è
$$ S(P)=96+216=312 $$
L'area sotto la funzione f(x) è sicuramente compresa tra la somma integrale inferiore e superiore.
$$ s(P)≤Area≤S(P) $$
ossia l'area è compresa tra 120 e 312
$$ 120≤Area≤312 $$
Dal punto di vista geometrico è un numero compreso nella differenza tra i rettangoli circoscritti e iscritti.
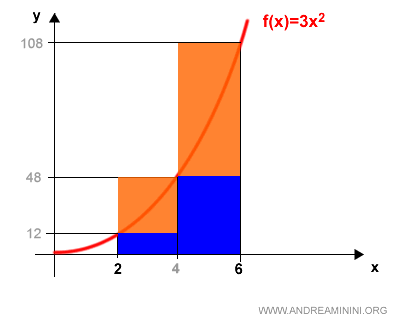
Per migliorare la stima prendo in considerazione anche un'altra partizione Q.
Questa volta la partizione suddivide l'intervallo [2,6] in 4 intervalli.
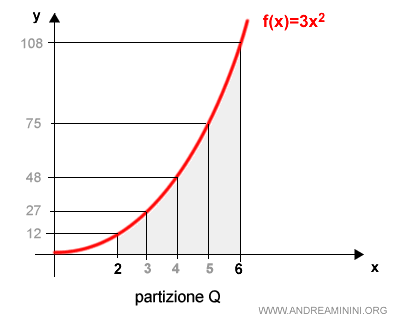
La partizione Q suddivide l'area in 4 rettangoli inscritti e 4 rettangoli circoscritti.
Analizzo i rettangoli inscritti.
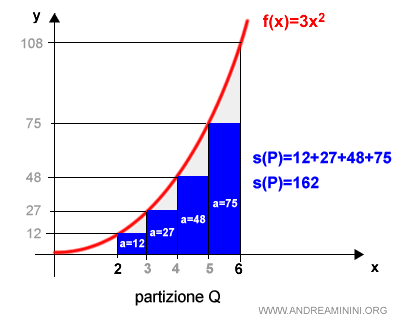
La somma integrale inferiore della partizione Q è
$$ s(Q)=162 $$
Analizzo i rettangoli circoscritti.
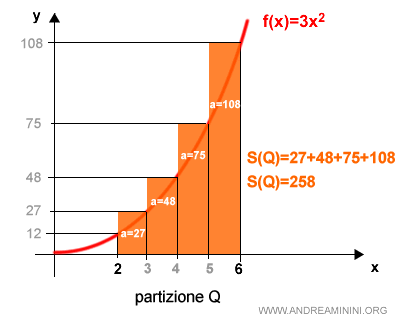
Quindi, la somma integrale superiore della partizione Q è
$$ S(Q)=258 $$
A questo punto ho le somme i di due partizioni P e Q.
$$ s(P)=120 \\ S(P) = 312 \\ s(Q) = 162 \\ S(Q) = 258 $$
Raccolgo le somme inferiori s(P) e s(Q) nell'insieme A
$$ A = \{ s(P) , s(Q) \} = \{ 120 , 162 \} $$
e le somme superiori S(P) e S(Q) nell'insieme B
$$ B = \{ S(P) , S(Q) \} = \{ 312 , 258 \} $$
L'estremo superiore dell'insieme A è 162 mentre l'estremo inferiore dell'insieme B è 258
$$ sup(A) = 162 \\ inf(B) = 258 $$
Quindi, secondo Riemann l'area del grafico è compresa tra 162 e 258
$$ sup(A) ≤Area≤ inf(B) $$
$$ 162≤Area≤258 $$
Continuando così con altre partizioni con intervalli sempre più piccoli, la stima dell'area diventa sempre più precisa.
Quando gli estremi sup(A) e inf(B) coincidono, ho trovato l'area del grafico ossia il risultato dell'integrale.
La formula fondamentale del calcolo integrale
Spesso non è necessario usare il metodo di esaustione per calcolare l'integrale. Esistono metodi molto più rapidi.
In particolar modo, si può usare la formula fondamentale del calcolo integrale.
$$ \int_a^b f(x) \:\:dx = F(b)-F(a) $$
La formula riconduce il calcolo dell'integrale definito alle primitive delle funzioni continue
Se conosco la primitiva F(x) della funzione integranda, la formula fondamentale del calcolo integrale mi permette di calcolare l'integrale definito in modo semplice e rapido.
Nota. Ci sono però degli handicap da considerare. La formula si applica soltanto se la funzione è derivabile. Inoltre, non è sempre facile trovare la primitiva di una funzione integranda.
Esempio
Posso risolvere il precedente esempio usando la formula fondamentale del calcolo integrale
$$ \int_2^6 3x^2 \:\: dx $$
La primitiva F(x) della funzione f(x) è
$$ F(x) = x^3 $$
perché la derivata prima F'(x) è uguale alla f(x)
$$ D [ x^3 ] = 3x^2 $$
L'integrale definito della funzione f(x) nell'intervallo [2,6] è pari a 208
$$ \int_2^6 3x^2 \:\: dx = F(6) - F(2) = (6)^3 - (2)^3 = 208 $$
In questo modo ho calcolato l'area compresa tra il grafico e l'asse delle ascisse senza suddividere l'area in rettangoli.
![l'area del grafico nell'intervallo [2,6]](http://www.andreaminini.org/data/andreamininiorg/integrale-funzione-derivata.gif)
E così via.
