Prodotto di un integrale per una costante
Il prodotto di un integrale definito della funzione f(x) nell'intervallo [a,b] per una costante k è uguale all'integrale del prodotto della funzione f(x) per la costante k.
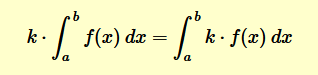
Questa proprietà degli integrali definiti è particolarmente utile nella risoluzione del calcolo integrale.
Un esempio pratico
Ho l'integrale definito della funzione f(x)=2x nell'intervallo [2,5]
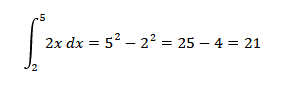
Provo a calcolare l'integrale della funzione moltiplicato per una costante k=2
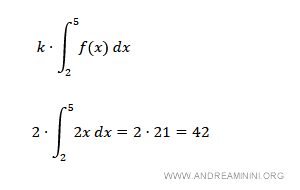
Ora calcolo l'integrale del prodotto della funzione per una costante k=2 nello stesso intervallo di integrazione [2,5].
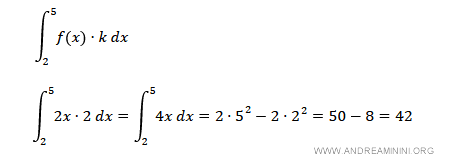
Il risultato è lo stesso.
Dimostrazione
Se una funzione f(x) è integrabile nell'intervallo [a,b] secondo Riemann allora per ogni ε>0 esiste una partizione P tale che la differenza tra la somma superiore e inferiore è minore di ε/2
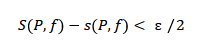
Nel caso della funzione f(x)⋅k con k≥1
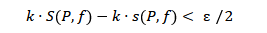
La relazione tra le somme integrali inferiori e superiori è
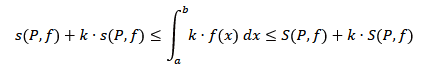
Ora va dimostrato che vale anche la seguente
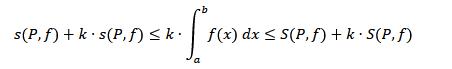
Calcolo la differenza tra le due disequazioni
![$$ s(P,f)+ k \cdot s(P,f) - [ S(P,f)+ k \cdot S(P,f) ] \le k \cdot \int_a^b f(x) \: dx - [ \int_a^b k \cdot f(x) \: dx ] \\ \le S(P,f) + k \cdot S(P,f) - [s(P,f)+ k \cdot s(P,f)] $$ $$ -ε/2 -ε/2 \le k \cdot \int_a^b f(x) \: dx - [ \int_a^b k \cdot f(x) \: dx ] \le ε/2 + ε/2 $$ $$ -ε \le k \cdot \int_a^b f(x) \: dx - [ \int_a^b k \cdot f(x) \: dx ] \le ε $$](http://www.andreaminini.org/data/andreamininiorg/prodotto-di-un-integrale-per-una-costante-1.gif)
Questo dimostra che per qualsiasi ε>0 arbitrario la relazione è soddisfatta.
E così via.
