L'integrale improprio
Gli integrali impropri sono integrali definiti su funzioni in un intervallo illimitato o su funzioni non limitate in un intervallo limitato.
Generalmente, un integrale definito è usato per studiare le funzioni limitate in un intervallo chiuso e limitato.
In tutti gli altri casi si parla di integrale improprio.
Integrale in un intervallo illimitato
Questo tipologia di integrali è caratterizzata da un intervallo di integrazione illimitato.
$$ \int_a^{+∞} f(x) \: dx $$
Esempio. Questa funzione integranda è limitata ma l'intervallo di integrazione è illimitato [a,∞).
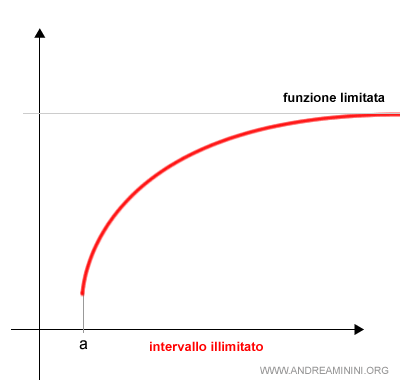
In questi casi l'integrale improprio è uguale al limite della funzione per x tendente all'estremo superiore dell'intervallo di integrazione ( infinito )
$$ \int_a^{+∞} f(x) \: dx = \lim_{b \rightarrow +∞} \int_a^b f(x) \: dx $$
che equivale a
$$ \int_a^{+∞} f(x) \: dx = \lim_{b \rightarrow +∞} [F(x)]_a^b $$
Se il limite
- esiste ed è un numero finito allora l'integrale improprio è convergente
- esiste ed è infinito allora l'integrale improprio è divergente
- non esiste allora l'integrale improprio è oscillante
Dimostrazione ( esistenza del limite )
Data una funzione continua e non negativa f(x)≥0
$$ \int_a^{+∞} f(x) \: dx = \lim_{b \rightarrow +∞} \int_a^b f(x) \: dx = \lim_{b \rightarrow +∞} F(b)-F(a) $$
Nel limite F è in funzione della variabile b→ ∞ mentre F(a) è un valore costante.
Quindi, si può considerare soltanto F(b)
$$ \lim_{b \rightarrow +∞} F(b) $$
Nota. Dove F(b) è la funzione primitiva rispetto all'estremo di integrazione b. $$ F(b) = \int f(b) \: dx $$ Quindi F'(b)=f(b).
La derivata della primitiva F(b) è la funzione stessa
$$ F'(b) = f(b) $$
Poiché la funzione f(b) è non negativa per l'ipotesi iniziale (f(x)≥0)
$$ f(b) \ge 0 $$
allora anche la funzione integrale è non negativa
$$ F'(b) = f(b) \ge 0 $$
Essendo la derivata prima maggiore di zero F'(b)≥0, allora la funzione F(b) è crescente nell'intervallo considerato [0,∞).
Se la funzione integrale F(b) è sempre crescente nell'intervallo [0,∞) allora esiste sicuramente anche il limite della funzione F(b) per b tendente a infinito.
$$ \lim_{b \rightarrow +∞} \int_a^b f(x) \: dx = \lim_{b \rightarrow +∞} F(b) - F(a) = \lim_{b \rightarrow +∞} F(b) $$
Questo dimostra l'esistenza del limite dell'integrale improprio in un intervallo illimitato
$$ \int_a^{+∞} f(x) \: dx = \lim_{b \rightarrow +∞} \int_a^b f(x) \: dx $$
Esempio 1
Questo integrale definito è improprio perché l'estremo superiore dell'intervallo di integrazione è illimitato (+∞)
$$ \int_1^{+∞} \frac{1}{x^2} \: dx $$
Calcolo il limite della funzione per x tendente b
$$ \lim_{b \rightarrow +∞} \int_1^b \frac{1}{x^2} \: dx $$
La primitiva della funzione è
$$ \lim_{b \rightarrow +∞} [ - \frac{1}{x} ]_1^b $$
$$ \lim_{b \rightarrow +∞} ( - \frac{1}{b} ) - ( - \frac{1}{1} ) $$
$$ \lim_{b \rightarrow +∞} - \frac{1}{b} + 1 = 1 $$
Il limite è uguale a 1
Nota. In generale, data una funzione $$ \int_1^{+∞} \frac{1}{x^k} \:dx $$ se k>1 il limite converge $$ \lim_{b \rightarrow ∞} ( \frac{b^{1-k}}{1-k} + \frac{1}{p-1} ) = \frac{1}{k-1} $$ se k<1 il limite diverge
Esempio 2
$$ \int_1^{+∞} \cos x \: dx $$
$$ \int_1^{+∞} \cos x \: dx = \lim_{b \rightarrow +∞} \int_1^b \cos x \: dx $$
$$ = \lim_{b \rightarrow +∞} [ \sin x ]_1^b $$
$$ = \lim_{b \rightarrow +∞} \sin b - \sin 1 = ind $$
In questo caso il limite non esiste perché sin ∞ è indeterminato.
Pertanto, l'integrale improprio è oscillante.
Funzione non limitata in un intervallo limitato
Questa tipologia di integrali impropri è calcolata su funzioni non limitate in un intervallo limitato.
$$ \int_a^b f(x) \: dx $$
Nota. Ad esempio, la funzione f(x) è definita in un intervallo limitato ma non è continua a un estremo di integrazione. Ad esempio la funzione è illimitata all'estremo superiore b. Quindi la funzione è definita nell'intervallo [a,b). Non è definita in [a,b].
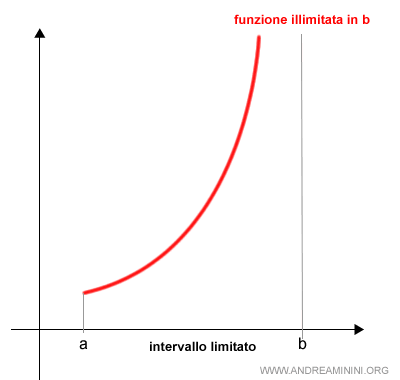
In questo caso, per calcolare il limite utilizzo il teorema del confronto degli integrali.
Nel limite dell'integrale improprio aggiungo all'estremo di integrazione una variabile h e la faccio tendere a zero da destra (0+).
$$ \int_a^b f(x) \: dx = \lim_{h \rightarrow 0+} \int_{a+h}^b f(x) \: dx $$
Adesso, nel limite la funzione è definita nell'intervallo [a+h,b]
Nota. In modo analogo se l'estremo in cui la funzione è illimitata fosse b scriverei $$ \int_a^b f(x) \: dx = \lim_{h \rightarrow 0+} \int_a^{b+h} f(x) \: dx $$ La logica è sempre la stessa. Ora la funzione è definita nell'intervallo [a,b+h].
A questo punto devo soltanto analizzare il risultato del limite.
- Se il limite esiste ed è finito, allora l'integrale improprio è convergente
- Se il limite esiste ed è infinito, allora l'integrale improprio è divergente
- Se il limite non esiste, allora l'integrale improprio è oscillante
Esempio
Questa funzione integranda è limitata nell'intervallo (0,1] ma non è definita sull'estremo inferiore 0.
$$ \int_0^1 \frac{1}{ \sqrt{x} } \: dx $$
Nota. In questo caso non posso calcolare il limite dell'integrale in questa forma. $$ \int_0^1 \frac{1}{ \sqrt{x} } \: dx = \lim_{a \rightarrow 0} \int_a^1 \frac{1}{ \sqrt{x} } \: dx $$ Perché nell'estremo a=0 la funzione è indefinita 1/0.
Calcolo il limite dell'integrale aggiungendo una variabile h tendente a zero.
$$ \int_0^1 \frac{1}{ \sqrt{x} } \: dx = \lim_{h \rightarrow 0+} \int_{0+h}^1 \frac{1}{ \sqrt{x} } \: dx $$
Calcolo la primitiva della funzione integranda
$$ = \lim_{h \rightarrow 0+} [ 2 \sqrt{x} ]_{0+h}^1 $$
Nota. La primitiva di una funzione nella forma 1/xn è $$ \int \frac{1}{x^n} = \frac{x^{1-n}}{1-n} $$
Poi svolgo i calcoli dell'integrale definito secondo la formula fondamentale dell'integrazione.
$$ = 2 \sqrt{1} - 2 \sqrt{0} $$
$$ = 2 \cdot 1 - 2 \cdot 0 $$
$$ = 2 $$
Il limite esiste ed è un numero finito, è uguale a 2.
Pertanto, l'integrale improprio è convergente.
$$ \int_0^1 \frac{1}{ \sqrt{x} } \: dx = 2 $$
E così via.
