Teorema di integrabilità delle funzioni continue
Se una funzione f(x) è una funzione continua nell'intervallo [a,b] allora la funzione è integrabile secondo Riemann in [a,b]
Dimostrazione
In base al teorema di Cantor una funzione limitata in un intervallo chiuso [a,b] è uniformemente continua.
Quindi è anche continua.
Fissato un ε>0 esiste un δ>0 tale che
$$ |f(x)-f(x')| < \frac{ε}{b-a} $$
per ogni coppia di punti x,x' ∈ [a,b] che rispetti la condizione
$$ |x-x'|<δ $$
Prendo in considerazione una generica partizione P della funzione nell'intervallo [a,b]
$$ P = ( x_0, x_1, x_2, ... , x_{n-1}, x_n ) $$
considerando x0=a e x1=b diventa
$$ P = ( a, x_1, x_2, ... , x_{n-1}, b ) $$
Il valore assoluto di ogni intervallo della partizione è minore di δ per la definizione iniziale
$$ |x_k-x_{k-1}| < δ $$
In ciascun intervallo xk,xk-1 individuo un valore minimo mk e massimo Mk della funzione f(x).
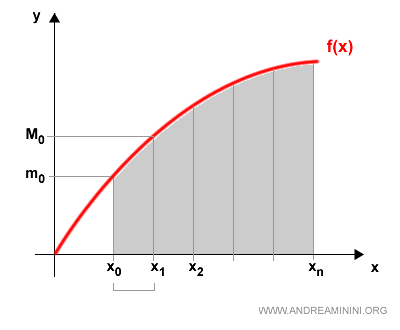
dove mk e Mk per k=1,...n sono
$$ m_k = inf[f(x): x \in [x_{k-1}, x_k] ] $$
$$ M_k = sup[f(x): x \in [x_{k-1}, x_k] ] $$
Pertanto, la relazione tra due punti qualsiasi di [a,b]
$$ |f(x)-f(x')| < \frac{ε}{b-a} $$
posso anche scriverla in questa forma equivalente
$$ M_k-m_k < \frac{ε}{b-a} $$
Nota. Ho eliminato il valore assoluto perché il valore massimo è per definizione maggiore (o al massimo uguale) al valore minimo. Quindi la differenza Mk-mk è sempre maggiore o uguale a zero.
Moltiplico entrambi i membri per xk - xk-1 ossia per la base del rettangolo considerato.
$$ ( M_k-m_k ) \cdot ( x_k - x_{k-1} ) < \frac{ε}{b-a} \cdot ( x_k - x_{k-1} ) $$
Il membro di sinistra è la differenza tra l'area del rettangolo Mk·(xk-xk-1) e l'area del rettangolo mk·(xk-xk-1).

Ripeto il calcolo per tutti i rettangoli della partizione P e sommo i risultati tra loro
$$ \sum_{k=1}^n ( M_k-m_k ) \cdot ( x_k - x_{k-1} ) < \frac{ε}{b-a} \cdot \sum_{k=1}^n ( x_k - x_{k-1} ) $$
Nel membro di sinistra ottengo la differenza tra la somma integrale inferiore e superiore
$$ S(p)-s(p) < \frac{ε}{b-a} \cdot \sum_{k=1}^n ( x_k - x_{k-1} ) $$
Dal punto di vista grafico
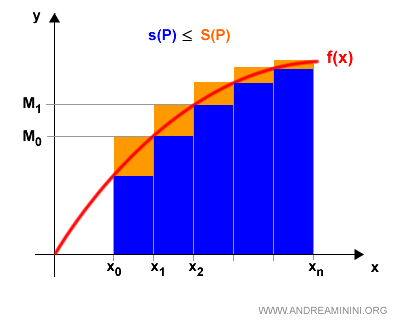
La sommatoria delle differenze xk - xk-1 per k=1,2,...,n è uguale alla differenza (b-a).
$$ S(p)-s(p) < \frac{ε}{b-a} \cdot (b-a) $$
quindi semplifico e ottengo la condizione dell'integrale di Riemann
$$ S(p)-s(p) < ε $$
Questo dimostra che ogni funzione continua in [a,b] è derivabile secondo Riemann.
E così via.
