L'unione delle partizioni in un integrale
Date due partizioni P e Q nell'intervallo [a,b], la partizione R che si ottiene unendo le partizioni $$ R = P ∪ Q $$ rispetta le seguenti diseguaglianze $$ s(P) \le s(R) \le S(R) \le S(Q) $$ dove s() indica le somme integrali inferiori e S() le somme integrali superiori.
La somma integrale è l'area dei plurirettangolo iscritto o circoscritto al grafico della funzione, ottenuto tramite una partizione.
Dimostrazione
La partizione P è composta da due punti consecutivi xk-1, xk.
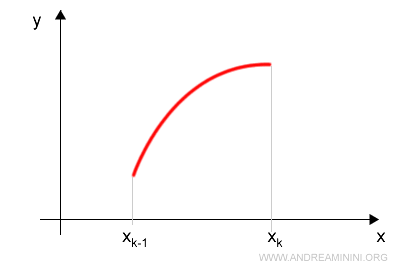
La partizione Q è composta da tre punti.
Un solo punto x in più rispetto alla partizione P.
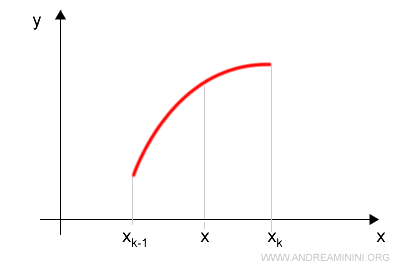
Quindi, l'unione delle due partizioni (R) è composta da tre punti
$$ R = P ∪ Q = { x_{k-1}, x, x_k } $$
e da due intervalli: [xk-1,x] e [x,xk]
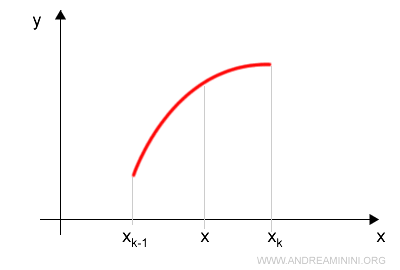
A questo punto calcolo le somme integrali inferiori e superiori per stabilire le relazioni d'ordine.
1] Le somme integrali inferiori
Individuo gli estremi inferiori in ogni intervallo della partizione R
$$ m_1 = \inf([x_{k-1}, x]) $$
$$ m_2 = \inf([x, x_k]) $$
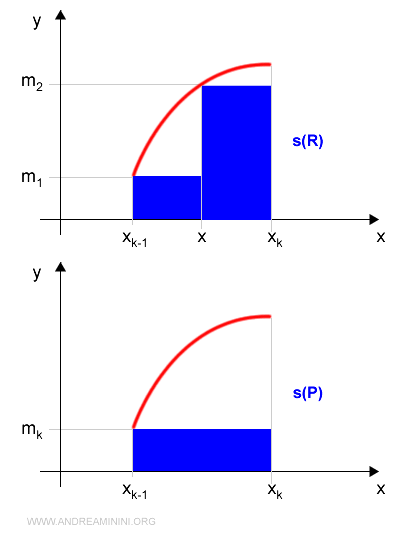
Dal punto di vista grafico
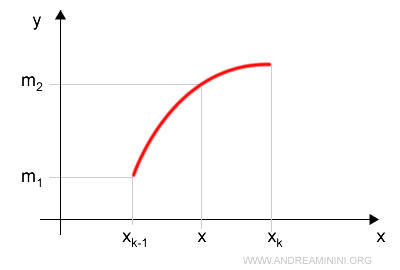
Le somme integrali inferiori s(R) e s(P) sono
$$ s(P) = m_k \cdot (x_k-x_{k-1}) $$
$$ s(R) = m_1 \cdot (x-x_{k-1}) + m_2 \cdot ( x_k - x ) $$
Ecco la rappresentazione grafica sul diagramma cartesiano
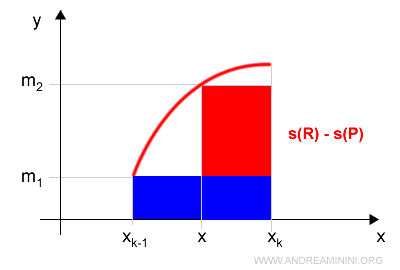
Pertanto, la differenza tra le due somme integrali s(R)-s(P) è
$$ s(R)-s(P) = [m_1 \cdot (x-x_{k-1}) + m_2 \cdot ( x_k - x )] - m_k \cdot (x_k-x_{k-1}) $$
Nota. Dal punto di vista geometrico è già evidente che la differenza s(R)-s(P) è maggiore di zero. Pertanto s(R) è maggiore di s(P). $$ s(R) \ge s(P) $$
Poiché
$$ m_1 \ge m_k $$
$$ m_2 \ge m_k $$
perché l'intervallo [xk-1,xk] contiene sia l'intervallo [xk-1,x] e sia l'intervallo [x,xk]
allora sostituendo mk a m1 e m2 si ottiene
$$ s(R)-s(P) \ge [m_k \cdot (x-x_{k-1}) + m_k \cdot ( x_k - x )] - m_k \cdot (x_k-x_{k-1}) $$
$$ s(R)-s(P) \ge m_k \cdot (x-x_{k-1} + x_k - x - x_k+x_{k-1}) $$
$$ s(R)-s(P) \ge m_k \cdot 0 $$
$$ s(R)-s(P) \ge 0 $$
Pertanto
$$ s(R) \ge s(P) $$
2] Le somme integrali superiori
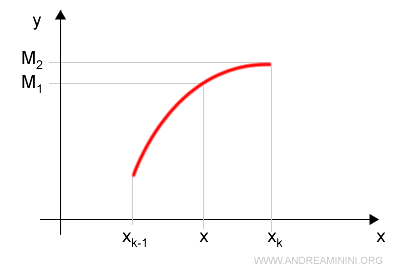
Ora calcolo gli estremi superiori in ogni intervallo della partizione R
$$ M_1 = \sup([x_{k-1}, x]) $$
$$ M_2 = \sup([x, x_k]) $$
Dal punto di vista grafico
Le somme integrali superiori S(R) e S(P) sono
$$ S(Q) = M_k \cdot (x_k-x_{k-1}) $$
$$ S(R) = M_1 \cdot (x-x_{k-1}) + M_2 \cdot ( x_k - x ) $$
Ecco la rappresentazione grafica
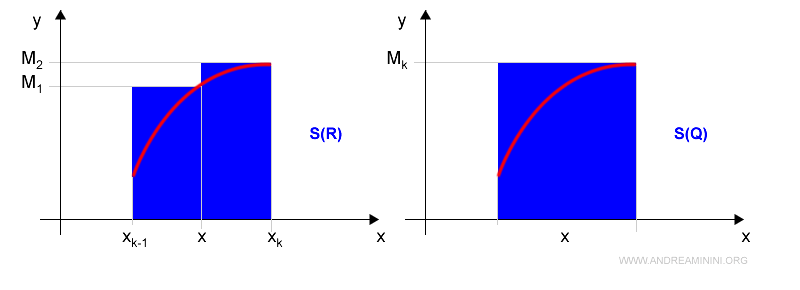
Pertanto, la differenza tra le due somme integrali superiori delle due partizioni S(Q)-S(P) è
$$ S(Q)-S(R) = M_k \cdot (x_k-x_{k-1}) - [M_1 \cdot (x-x_{k-1}) + M_2 \cdot ( x_k - x )] $$
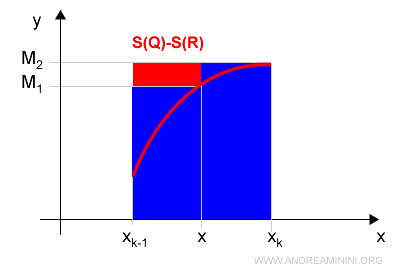
Nota. Dal punto di vista geometrico è subito evidente che la differenza S(Q)-S(R) è maggiore di zero. Pertanto, la somma integrale superiore S(Q) è maggiore di S(R). $$ S(Q) \ge S(R) $$
Poiché
$$ m_1 \le m_k $$
$$ m_2 \le m_k $$
allora sostituendo Mk a m1 e m2 si ottiene
$$ S(Q)-S(R) \ge M_k \cdot (x_k-x_{k-1}) - [M_k \cdot (x-x_{k-1}) + M_k \cdot ( x_k - x )] $$
$$ S(Q)-S(R) \ge M_k \cdot (x_k-x_{k-1} - x+x_{k-1}- x_k + x ) $$
$$ S(Q)-S(R) \ge M_k \cdot ( 0 ) $$
$$ S(Q)-S(R) \ge 0 $$
Pertanto
$$ S(Q) \ge S(R) $$
3] In conclusione
Analizzando le somme integrali inferiori e superiori ho stabilito che
$$ s(R) \ge s(P) $$
$$ S(Q) \ge S(R) $$
Le somme integrali superiori sono sempre maggiori delle somme integrali inferiori.
Quindi, posso unire le due relazioni d'ordine in questa forma
$$ S(Q) \ge S(R) \ge s(R) \ge s(P) $$
ossia
$$ s(P) \le s(R) \le S(R) \le S(Q) $$
che dimostra la proposizione iniziale
E così via.
