Il criterio del confronto degli integrali impropri
- Date due funzioni f(x) e g(x) definite nell'intervallo [0,∞) tali che $$ 0 \le f(x) \le g(x) $$ secondo la proprietà del confronto gli integrali sono $$ 0 \le \int_a^b f(x) \:dx \le \int_a^b g(x) \: dx $$
- Se l'integrale improprio di g(x) è convergente, allora anche l'integrale improprio di f(x) è convergente.
- Se l'integrale improprio di f(x) è divergente, allora anche l'integrale improprio di g(x) è divergente.
Dimostrazione e spiegazione
Ho due funzioni f(x) e g(x) definite nell'intervallo [a,b].
$$ f(x) \le g(x) $$
Secondo la proprietà del confronto gli integrali sono
$$ \int_a^b f(x) \:dx \le \int_a^b g(x) \: dx $$
Caso 1
Se esiste il limite per b tendente a infinito del secondo integrale ed è un numero finito l, ossia l'integrale di g(x) è convergente.
$$ l = \lim_{b \rightarrow ∞} \int_a^b g(x) \: dx $$
allora il primo limite deve essere minore o uguale a l.
$$ \lim_{b \rightarrow ∞} \int_a^b f(x) \: dx \le l $$
Quindi anche l'integrale di f(x) è convergente.
Caso 2
Se il primo limite esiste ed è infinito, ossia l'integrale di g(x) è divergente
$$ \lim_{b \rightarrow ∞} \int_a^b f(x) \: dx = ∞ $$
allora anche il secondo limite deve essere infinito perché g(x)≥f(x).
$$ \lim_{b \rightarrow ∞} \int_a^b g(x) \: dx \ge ∞ $$
Quindi, anche l'integrale di g(x) è divergente.
$$ \lim_{b \rightarrow ∞} \int_a^b g(x) \: dx = ∞ $$
Un esempio pratico
Devo capire se l'integrale improprio della funzione f(x)=e-x2 è convergente nell'intervallo [0,∞)
$$ \int_0^∞ e^{-x^2} \: dx $$
Nota. Se calcolassi il limite non riuscirei a capirlo facilmente $$ \int_0^∞ e^{-x^2} \: dx = \lim_{b \rightarrow +∞ } \int_0^∞ e^{-x^2} $$ perché la funzione primitiva non è elementare.
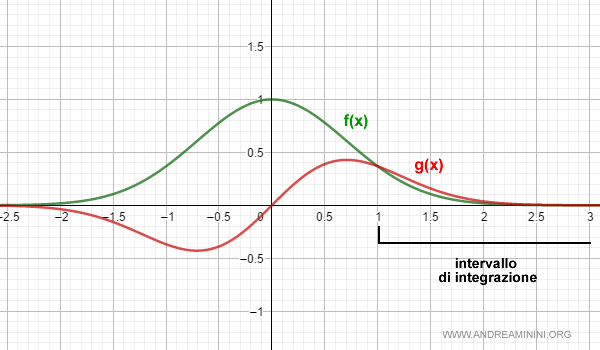
Prendo in considerazione un intervallo di integrazione più piccolo [1,∞) e un'altra funzione g(x)=e-x2·x
$$ \int_1^∞ e^{-x^2} \cdot x \: dx $$
Nell'intervallo [1,∞] la g(x) è maggiore o uguale alla f(x)
$$ e^{-x^2} \le e^{-x^2} \cdot x $$
Per la proprietà del confronto degli integrali vale
$$ \int_1^∞ e^{-x^2} \: dx \le \int_1^∞ e^{-x^2} \cdot x \: dx $$
Nel secondo integrale è più facile calcolare la primitiva
$$ \int_1^∞ e^{-x^2} \cdot x \: dx = \lim_{ b \rightarrow ∞ } \int_1^b e^{-x^2} \cdot x \: dx $$
$$ = \lim_{ b \rightarrow ∞ } [ - \frac{1}{2} e^{-x^2} ]_1^b $$
$$ = \lim_{ b \rightarrow ∞ } - \frac{1}{2} e^{-b^2} + \frac{1}{2} e^{-1^2} $$
$$ = \lim_{ b \rightarrow ∞ } - \frac{1}{2} e^{-b^2} + \frac{1}{2e} $$
$$ = 0 + \frac{1}{2e} $$
$$ = \frac{1}{2e} $$
Quindi, l'integrale improprio della g(x) converge a 1/2e.
$$ \int_1^∞ e^{-x^2} \cdot x \: dx = \frac{1}{2e} $$
Poiché vale la disequazione
$$ \int_1^∞ e^{-x^2} \: dx \le \int_1^∞ e^{-x^2} \cdot x \: dx $$
$$ \int_1^∞ e^{-x^2} \: dx \le \frac{1}{2e} $$
Posso dedurre che anche l'integrale improprio della f(x) è convergente.
E così via.
