Il metodo di integrazione numerica di Eulero

Il metodo di integrazione numerica di Eulero mi permette di stimare il risultato di un integrale definito della funzione y=f(t) tramite un algoritmo iterativo $$ \int_a^b f(t) \ dt $$ una volta scelto un dato iniziale y₀, t₀. $$ y_j = y_{j-1} + \frac{dy}{dt}|_{t=j-1} \cdot \Delta t $$ Dove Δt è il passo di integrazione $$ t_j = t_{j-1} + \Delta t $$

Dato un integrale generico nell'intervallo di integrazione [a,b]

$$ \int_a^b f(t) \ dt $$

suddivido l'intervallo di integrazione in n parti ottenendo il passo di integrazione

$$ \Delta t = \frac{b-a}{n} $$

Poi scelgo un punto iniziale t₀ e calcolo il valore della funzione f(t) in t₀

$$ y_0 = f(0) $$

Per stimare la posizione successiva applico la seguente formula

$$ y_1 = y_0 + \frac{dy}{dt}|_{t=t0} \cdot \Delta t $$

In pratica, moltiplico la derivata della funzione nel punto t₀ per il passo di integrazione, ottenendo una stima della funzione nel punto t₁.

Nota. Trattandosi di una stima il risultato non è preciso e l'errore tende ad accumularsi in modo sistematico nel corso dell'integrazione.

La spiegazione

Per spiegare questo metodo utilizzo il grafico di una funzione y=f(t) nell'intervallo [a,b]

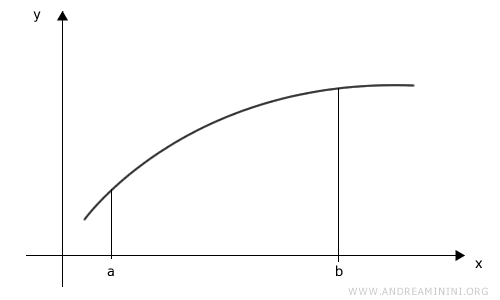
Suddivido l'intervallo [a,b] di integrazione in una partizione di tre intervalli (n=3).

$$ \Delta x = \frac{b-a}{n} $$

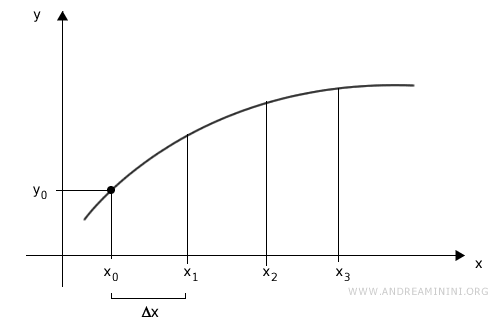
Ogni intervallo ha la stessa ampiezza Δx

Nota. Per spiegare il metodo farò un esempio banale con soli tre intervalli. Quindi, il risultato finale sarà molto impreciso. Questo metodo è accurato solo se il numero degli intervalli è sufficientemente grande.

Scelgo come punto iniziale x₀ e utilizzo la funzione f(x) per ottenere il corrispondente valore di y₀.

Quindi, i dati iniziali del computo sono x₀ e y₀.

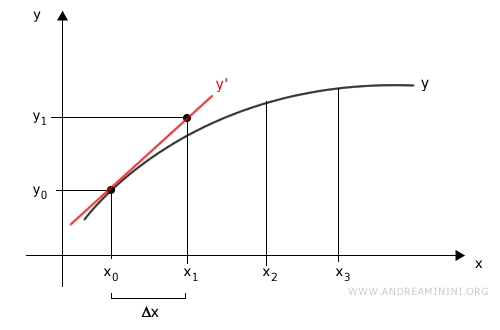
A questo punto, calcolo il punto successivo (x₁,y₁)

$$ \begin{cases} x_1 = x_0 + \Delta x \\ \\ y_1 = y_0 + \frac{dy}{dx} |_{x=x_0} \cdot \Delta x \end{cases} $$

Pertanto, calcolo la derivata della funzione nel punto f(x₀), ossia la retta tangente nel punto (x₀,y₀) fino a farla intersecare con la retta perpendicolare a x₁.

In questo modo trovo la stima del punto (x₁,y₁)

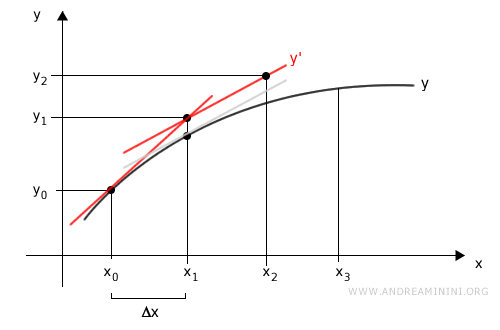
Itero di nuovo il calcolo per trovare il punto successivo (x₂,y₂)

$$ \begin{cases} x_2 = x_1 + \Delta x \\ \\ y_2 = y_1 + \frac{dy}{dx} |_{x=x_1} \cdot \Delta x \end{cases} $$

In questo caso devo calcolare la derivata della funzione nel punto f(x₁) e traslo la retta tangente facendola passare nel punto (x₁,y₁) individuato precedentemente.

In questo modo trovo anche la stima del punto (x₂,y₂)

Infine, ripeto gli stessi calcoli per trovare l'ultimo punto (x₃,y₃)

$$ \begin{cases} x_3 = x_2 + \Delta x \\ \\ y_3 = y_2 + \frac{dy}{dx} |_{x=x_2} \cdot \Delta x \end{cases} $$

In questo caso calcolo la derivata della funzione nel punto f(x₂) e traslo la retta tangente facendola passare nel punto (x₂,y₂) individuato precedentemente.

In questo modo trovo anche la stima del punto (x₃,y₃)

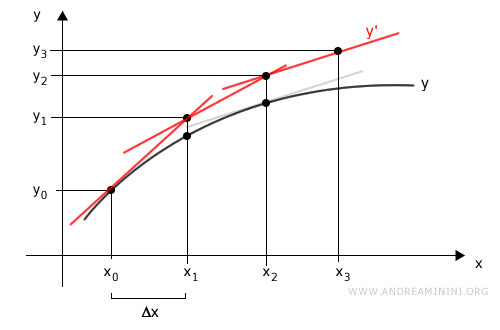
Ho trovato una stima lineare y* della funzione f(x).

Questo mi permette di calcolare l'area tra la funzione stimata y* e l'asse x, ossia l'integrale definito nell'intervallo [a,b] sommando le aree negli intervallo [x₀,x₁] , [x₁,x₂] , [x₂,x₃].

Essendo una funzione lineare, per trovare le aree degli intervalli basta calcolare l'area di un rettangolo e di un triangolo.

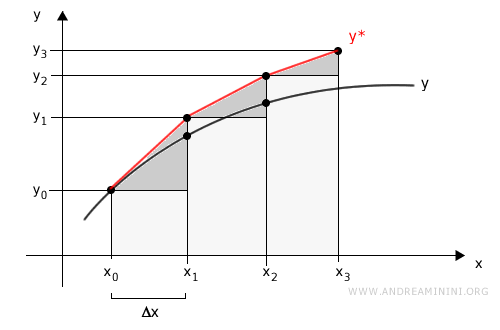
La somma delle aree mi fornisce una stima dell'integrale della funzione f(x) nell'intervallo [a,b]

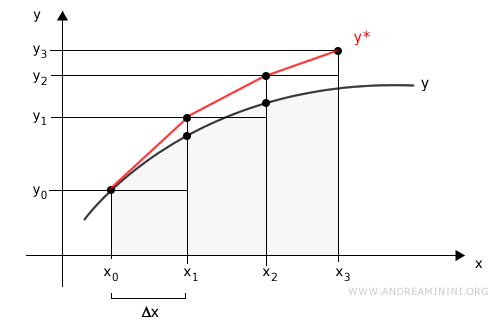
E così via.