Il calcolo integrale
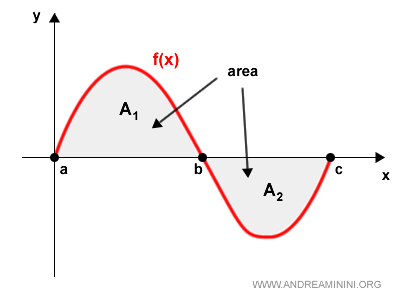
L'integrale è un operatore usato in analisi matematica per calcolare l'area tra il grafico di una funzione e l'asse delle ascisse.
Il calcolo integrale venne usato per la prima volta da Archimede ed Eudosso di Cnido, nel IV secolo a.C., con il metodo di esaustione per calcolare l'area delle superfici irregolari.
Si chiama metodo di esaustione perché l'area viene riempita con dei poligoni regolari.
Come funziona il metodo per esaustione
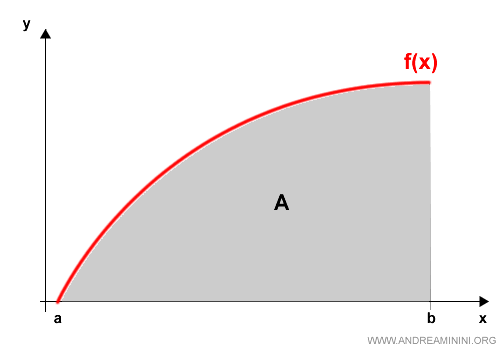
Devo misurare l'area sotto una parabola compresa nell'intervallo [a,b]
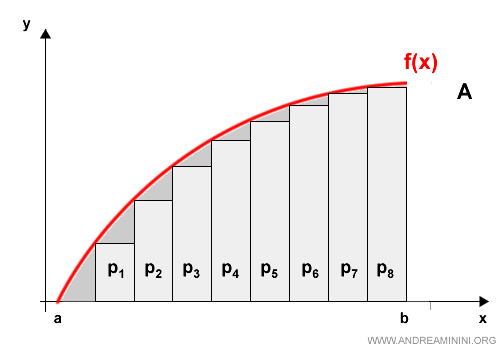
Suddivido la superficie in n poligoni iscritti.
In questo esempio sono otto poligoni iscritti: p1,p2,...,p8.
L'area dei poligoni regolari è molto più semplice da calcolare
La somma delle aree dei poligoni Amin mi fornisce una stima dell'area della parabola per difetto.
$$ A_{min} = \sum_0^n A(p_n) $$
Ora suddivido la superficie in n poligoni circoscritti.
In questo caso i poligoni regolari sono esterni alla parabola.
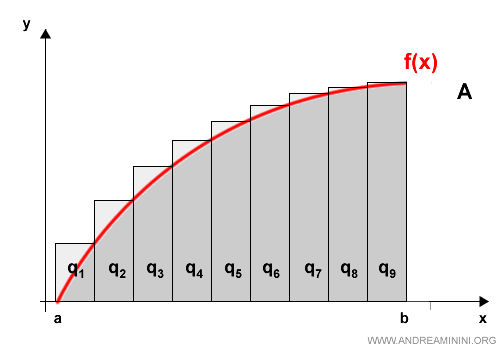
Poi calcolo l'area degli n poligoni regolari da q1 a q9.
Ottengo così una stima Amax dell'area della parabola per eccesso.
$$ A_{max} = \sum_0^n A(p_n) $$
L'area della parabola A è sicuramente compresa tra le due stime.
$$ A_{min} \le A \le A_{max} $$
Nota. La stima è tanto più precisa, quanti più poligoni utilizzo per riempire l'area della parabola. Facendo tendere il numero dei poligoni regolari n a infinito, la differenza tra Amin e Amax si riduce e la somma delle aree dei poligoli Amin≅Amax tende a eguagliare l'area della parabola. $$ \lim_{n \rightarrow ∞} A_{min} = \lim_{n \rightarrow ∞} A_{max} = A $$
La differenza tra integrale definito e indefinito
Esistono due tipi di integrali
- Integrale definito
L'integrale è calcolato entro un intervallo di integrazione (a,b) della funzione. E' il calcolo usato per misurare l'area. Pertanto, è un numero. $$ \int_a^b f(x) \:\:dx $$ - Integrale indefinito
L'integrale è calcolato su tutto l'intervallo di definizione della funzione. E' l'operatore inverso della derivata di una funzione. Pertanto, è una funzione o per meglio dire una famiglia di funzioni. $$ \int f(x) \:\:dx $$
Nota. L'integrale definito e indefinito hanno scopi e metodi di calcolo differenti. Pertanto, non vanno confusi tra loro.
Teorema fondamentale del calcolo integrale
Data una funzione continua nell'intervallo [a,b], la funzione integrale F(x) $$ F(x) = \int_a^x f(t) \: dt = $$ è derivabile e la derivata vale f(x) $$ D[F(x)]= f(x) $$
La funzione F(x) è detta funzione primitiva di f(x).
Il teorema fondamentale del calcolo integrale definisce una relazione tra integrali e derivate
Un esempio pratico
Nell'intervallo [0,x] l'integrale della funzione 2t è x2
$$ F(x) = \int_0^x 2t \: dt = x^2 $$
La funzione integranda f(x) è
$$ f(x) = 2x $$
La funzione integrale F(x) è
$$ F(x)=x^2 $$
La derivata della funzione integrale F'(x) è
$$ F'(x)=D[x^2]=2x $$
Quindi, la derivata della funzione integrale F'(x) è uguale alla funzione integranda f(t) calcolata per t=x.
$$ F'(x)=f(x) $$
Questa proprietà vale in generale per tutte le funzioni f(x) continue in un intervallo [a,b].
Dimostrazione e spiegazione
Per ottenere la derivata della funzione integrale devo calcolare il limite del rapporto incrementale della funzione primitiva F(x) per h→0
$$ \lim_{h \rightarrow 0} \frac{F(x+h)-F(x)}{h} $$
$$ \lim_{h \rightarrow 0} \frac{1}{h} \cdot [ F(x+h)-F(x) ] $$
$$ \lim_{h \rightarrow 0} \frac{1}{h} \cdot [ \int_a^{x+h} f(t) \:dt - \int_a^{x} f(t) \:dt ] $$
Per la proprietà additiva degli integrali rispetto all'intervallo, posso suddividere l'intervallo di integrazione [a,x+h] in due partizioni [a,x] e [x, x+h].
$$ \lim_{h \rightarrow 0} \frac{1}{h} \cdot [ \int_a^{x} f(t) \:dt + \int_x^{x+h} f(t) \:dt - \int_a^{x} f(t) \:dt ] $$
$$ \lim_{h \rightarrow 0} \frac{1}{h} \cdot [ \int_x^{x+h} f(t) \:dt ] $$
Nota. Secondo il teorema della media dell'integrale in una funzione f(x) continua nell'intervallo [a,b] esiste un punto x0∈[a,b] tale che $$ \int_a^b f(t) \:dt = f(x_0) \cdot (b-a) $$ Quindi $$ \int_x^{x+h} f(t) \:dt = f(x_0) \cdot ((x+h)-x) $$ Quindi $$ \int_x^{x+h} f(t) \:dt = f(x_0) \cdot (h) $$ Ora, calcolando il limite per h→0 il valore di h(x) tende a x.
$$ \lim_{h \rightarrow 0} \frac{1}{h} \cdot f(x_0) \cdot (h) $$
$$ \lim_{h \rightarrow 0} f(x_0) $$
Il punto x0 dipende dall'incremento h perché x0∈(x,x+h).
Quindi il limite per h→0 fa tendere x0 a x.
$$ \lim_{h \rightarrow 0} f(x_0) = f(x) $$
Questo dimostra la relazione tra la funzione integranda f(x) e la derivata della funzione integrale F(x).
E così via.
