Integrale doppio

Un integrale doppio è un'estensione del concetto di integrale definito a due variabili $ f(x, y) $, ed è usato per calcolare il volume sotto una superficie sotto la superficie $ z = f(x, y) $ e sopra la regione $ D $ nel piano. \[\iint_D f(x, y)\, dA\] Dove $ dA $ rappresenta un elemento infinitesimo di area nella regione $ D $ e può essere scritto come $ dx\,dy $ o $ dy\,dx $, a seconda dell'ordine di integrazione.

In generale, l'integrale doppio $ \iint_D f(x, y)\, dA $ rappresenta il volume del solido compreso tra la superficie superiore: $ z = f(x, y) $ e la regione $ D $ nel piano $ xy $ inferiore $ z = 0 $.

Questo vale quando $ f(x, y) \geq 0 $ su tutta la regione $ D $.

Se invece la funzione assume anche valori negativi, l'integrale doppio misura il la differenza algebrica tra le parti positive (sopra il piano $ z = 0 $) e quelle negative (sotto il piano).

Come si calcola

Spesso si calcola come un integrale iterato, cioè:

\[ \iint_D f(x, y)\, dA = \int_a^b \left( \int_{g_1(x)}^{g_2(x)} f(x, y)\, dy \right) dx \]

oppure invertendo l'ordine:

\[ \iint_D f(x, y)\, dA = \int_c^d \left( \int_{h_1(y)}^{h_2(y)} f(x, y)\, dx \right) dy \]

La scelta dell'ordine dipende dalla forma della regione $ D $: a volte conviene integrare prima in $ y $, a volte in $ x $.

In altre parole, posso scegliere l'ordine di integrazione più conveniente per il calcolo, a condizione che la regione di integrazione sia descritta correttamente in base a quell'ordine.

Nota. È importante sottolineare che invertire i limiti di integrazione (ad esempio, da x a y invece che da y a x) potrebbe introdurre un segno negativo nell'integrale. Pertanto, è essenziale mantenere l'ordine corretto dei limiti per garantire il segno appropriato del risultato.

Un esempio pratico

Considero la funzione di due variabili $ f(x, y) = x + y $ sopra un'area rettangolare $ D = [0,1] \times [0,2] $ del piano.

L'integrale doppio è

\[ \iint_D (x + y)\, dA = \int_0^1 \left( \int_0^2 (x + y)\, dy \right) dx \]

Come primo passo integro la funzione rispetto alla variabile $ y $:

\[ \int_0^2 (x + y)\, dy = \left[ xy + \frac{y^2}{2} \right]_0^2 = 2x + 2 \]

Poi rispetto integro rispetto alla variabile $ x $:

\[ \int_0^1 (2x + 2)\, dx = \left[ x^2 + 2x \right]_0^1 = 1 + 2 = 3 \]

In questo caso, il valore dell’integrale doppio è 3, è il volume sotto la superficie $ z = x + y $ e sopra il rettangolo $ D = [0,1] \times [0,2] $ nel piano $ xy $.

Ecco la rappresentazione 3D della funzione $ z=x+y $ sopra la regione rettangolare $ D=[0,1]×[0,2] $.

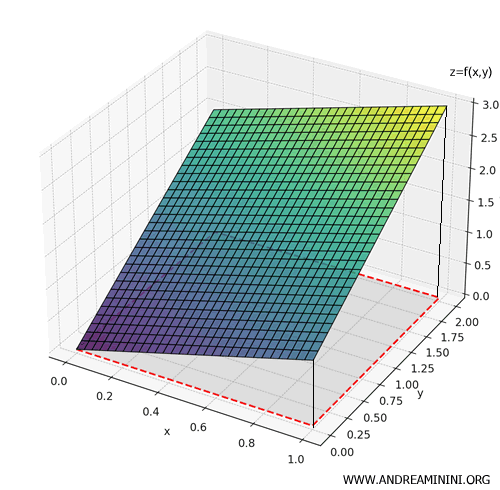
esempio

L’area di integrazione è la base grigia $ D=[0,1]×[0,2] $, mentre il solido colorato tra questa base e la superficie rappresenta il volume = 3 calcolato con l’integrale doppio.

Esempio 2

Considero nuovamente la funzione $ f(x, y) = x + y $ ma prendo come regione di integrazione:

\[ D = [-1, 1] \times [-1, 1] \]

In questa regione, la funzione $ x + y $ assume:

valori positivi se $ x + y > 0 $
valori negativi se $ x + y < 0 $
valore nullo (zero) sulla retta $ x + y = 0 $

Ora calcolo l'integrale

\[ \iint_D (x + y)\, dA = \int_{-1}^{1} \int_{-1}^{1} (x + y)\, dy\,dx \]

Integro rispetto a $ y $:

\[ \int_{-1}^{1} (x + y)\, dy = \left[ xy + \frac{y^2}{2} \right]_{-1}^1 = x(1) + \frac{1}{2} - x(-1) - \frac{1}{2} = 2x \]

Poi integro rispetto a $ x $:

\[ \int_{-1}^{1} 2x\, dx = \left[ x^2 \right]_{-1}^1 = 1 - 1 = 0 \]

Anche se la funzione $ x + y $ non è nulla sulla regione $ D $, l’integrale doppio vale zero, perché le aree sopra e sotto il piano $ z = 0 $ si annullano perfettamente.

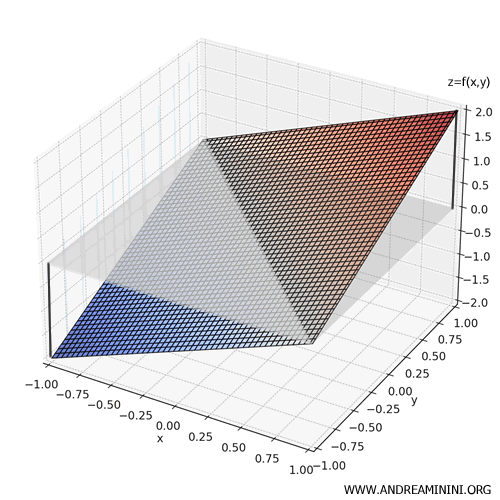
esempio

Questo esempio dimostra che l'integrale doppio non rappresenta sempre un vero e proprio volume, ma una differenza algebrica tra due regioni sopra e sotto il piano $ z = 0 $.

Può rappresentare il volume solo se la funzione è sempre positiva (o sempre negativa) nell'area di integrazione.

E così via